Трехфазных обмоток трансформатора

В общем случае 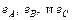в фазных обмотках 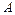, и 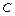несинусоидальны. Предполагая наличие только нечетных гармонических и принимая начальную фазу 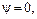имеем для обмотки :

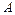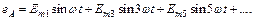
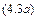
Соответственно для фаз и имеем:

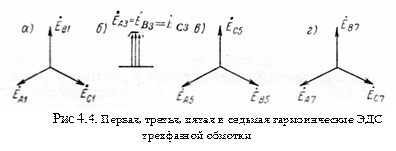
Из уравнений (4.3 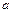), (4.3 б), (4.З в) мы видим, что а) первые гармонические в фазах 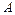, и 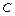образуют симметричную трехлучевую звезду с порядком следования фаз 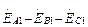(рис. 4.4, а; б) третьи гармонические и соответственно гармонические, кратные трем, во всех трех фазных обмотках совпадают по фазе (рис. 4.4, б) и, следовательно, независимо от способа соединения обмоток направлены в каждой фазной обмотке либо от ее начала к ее концу, либо в обратном направлении; в) пятая и седьмая гармонические образуют такие же, как первая гармоническая, симметричные трехлучевые звезды, но по сравнению с первой пятая гармоническая имеет обратный порядок следования фаз (рис. 4.4, в,) а седьмая гармоническая – тот же порядок следования фаз, что и первая (рис. 4.4, г). В общем случае гармонические порядка 3с+1, где с - любое четное число, имеют тот же порядок следования фаз, что и первая гармоническая, получаемая при 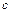= 0, а гармонические порядка Зс-1 – обратный порядок.

Дата добавления: 2014-03-11; просмотров: 559; Нарушение авторских прав

Мы поможем в написании ваших работ!