
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Примеры потенциальной энергии
1) Найдем потенциальную энергию для силы гравитационного взаимодействия. Пусть 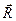 – радиус-вектор точки m2 в системе отсчёта, связанной с точкой m1. Тогда вектор гравитационной силы, действующей на материальную точку m2, направлен противоположно
– радиус-вектор точки m2 в системе отсчёта, связанной с точкой m1. Тогда вектор гравитационной силы, действующей на материальную точку m2, направлен противоположно 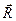 :
: 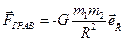 , где
, где 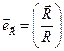 - единичный вектор направления для вектора
- единичный вектор направления для вектора 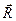 . Т.к. сила гравитации – консервативная, то должно выполняться равенство:
. Т.к. сила гравитации – консервативная, то должно выполняться равенство:
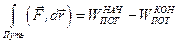 .
.
Этот интеграл не должен зависеть от траектории, поэтому будем интегрировать вдоль радиус-вектора 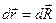 . Векторы
. Векторы 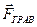 и
и 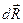 направлены противоположно, поэтому
направлены противоположно, поэтому
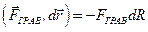 .
.
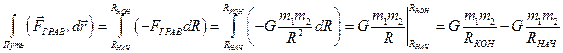 .
.
Сравниваем: 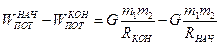 .
.
Следовательно, потенциальная энергия гравитационного взаимодействия материальных точек определяется выражением:
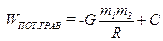 .
.
Обратите внимание на знак минус! (Обычно принимают, что С=0.)
2) Для силы тяжести 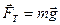 потенциальная энергия WП = mgh.
потенциальная энергия WП = mgh.
 Здесь высота h определяется выбором начала отсчета энергии.
Здесь высота h определяется выбором начала отсчета энергии.
Проверим соотношение 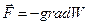 .
.
В системе отсчёта, связанной с Землёй , введем систему координат так, чтобы ось z была направлена вверх (против вектора силы тяжести), тогда потенциальная энергия тела равна 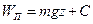 , где С определяется началом отсчета координаты z.
, где С определяется началом отсчета координаты z.
Эквипотенциальная поверхность – горизонтальная плоскость z=const , поэтому вектор силы должен быть направлен ей перпендикулярно, т.е. вертикально. Величина энергии увеличивается вверх, поэтому вектор силы должен быть направлен вниз. Действительно, 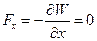 ,
, 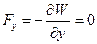 ,
, 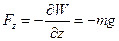 . Т.е. вектор силы
. Т.е. вектор силы 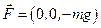 в этой системе координат действительно направлен вертикально вниз.
в этой системе координат действительно направлен вертикально вниз.
3) Для силы кулоновского взаимодействия: 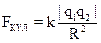 потенциальная энергия:
потенциальная энергия:
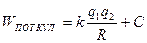 .
.
(Обычно С=0. В случае если заряды разного знака, то потенциальная энергия отрицательна.)
4) Для силы упругости 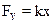 потенциальная энергия:
потенциальная энергия: 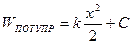 . (Обычно С=0.)
. (Обычно С=0.)
Потенциальная энергия для обобщенного закона Гука.
Из соотношений 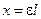 ,
, 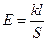 , получаем
, получаем 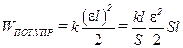 .
.
Учитывая, что объём деформируемого тела 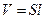 , находим энергию при возникновении относительной деформации величиной e:
, находим энергию при возникновении относительной деформации величиной e:
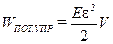 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Свойства градиента функции | | | ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ |
Дата добавления: 2014-03-11; просмотров: 719; Нарушение авторских прав

Мы поможем в написании ваших работ!