
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Напряженность электрического поля в диэлектрике. Диэлектрическая проницаемость
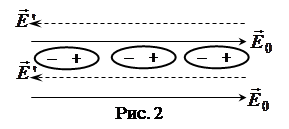
Итак, при внесенции диэлектрика в электрическое поле с напряженностью 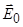 происходит поляризация диэлектрика, в результате которой возникает поле связанных зарядов, направленное против внешнего поля (см. рис. 2).
происходит поляризация диэлектрика, в результате которой возникает поле связанных зарядов, направленное против внешнего поля (см. рис. 2).
Напряженность поля связанных зарядов обозначим через 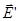 ; оказывается она пропорциональна напряженности поля в диэлектрике, т.е.
; оказывается она пропорциональна напряженности поля в диэлектрике, т.е. 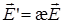 поэтому напряженность поля в диэлектрике
поэтому напряженность поля в диэлектрике 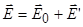 , или
, или 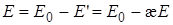 .
.
 откуда
откуда 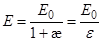 (3)
(3)
где 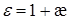 (4)
(4)
называют относительной диэлектрической проницаемостью вещества или среды; 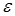 - безразмерная величина; т.к. æ =0 для вакуума и, практически, для воздуха, то для этих же сред
- безразмерная величина; т.к. æ =0 для вакуума и, практически, для воздуха, то для этих же сред 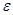 = 1.
= 1.
Итак, поле в диэлектрике ослабляется в ε раз, по сравнению с полем в вакууме. Из рис. 2 следует, что связанный суммарный заряд не равен нулю лишь на поверхности диэлектрика. Эти заряды называются поверхностными поляризационными зарядами.
4.4. Теорема Гаусса - Остроградского для поля в диэлектрике. Связь векторов 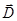 - смещения,
- смещения, 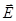 - напряженности и
- напряженности и 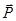 - поляризованности
- поляризованности
Теорема Гаусса - Остроградского для потока вектора 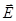 в вакууме имела вид:
в вакууме имела вид:
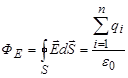 , или
, или 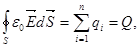
где Q - суммарный заряд, охватываемый замкнутой поверхностью S. В диэлектрике Q складывается из свободных (сторонних) зарядов и связанных зарядов, т.е.
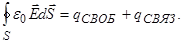 (5)
(5)
Можно показать, что 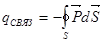 .
.
Подставляя эту формулу в (5), после преобразования получим
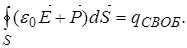 (6)
(6)
Величину 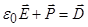 (7)
(7)
называют вектором электрического смещения или вектором электрической индукции. Она измеряется, как и 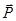 , в Кл/м2. Учитывая, что
, в Кл/м2. Учитывая, что 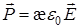 находим
находим
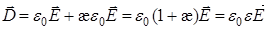 . (8)
. (8)
Линии вектора 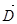 могут начинаться или заканчиваться лишь на свободных зарядах, а линии
могут начинаться или заканчиваться лишь на свободных зарядах, а линии 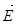 - на свободных и связанных. С учетом (7) формула (6) запишется так
- на свободных и связанных. С учетом (7) формула (6) запишется так
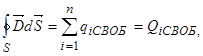 , (9)
, (9)
т.е. поток вектора электрического смещения через произвольную замкнутую поверхность S равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью.
Это и есть теорема Гаусса - Остроградского в интегральной форме для поля в диэлектрике, которая в дифференциальной форме выглядит так:
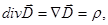
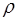 = dq/dV, Кл / м
= dq/dV, Кл / м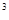 (10)
(10)
ρ – объемная плотность свободных зарядов.
4.5. Граничные условия для векторов 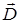 и
и 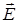
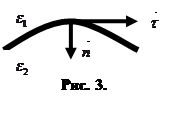 Из теоремы Гаусса-Остроградского (9) для поля в диэлектрике, на границе раздела двух диэлектриков, (см. рис. 3), имеем
Из теоремы Гаусса-Остроградского (9) для поля в диэлектрике, на границе раздела двух диэлектриков, (см. рис. 3), имеем 
откуда 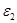 E
E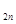 =
= 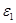 E
E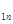 .
. 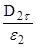 =
= 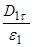 , откуда Е
, откуда Е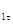 = Е
= Е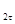 .
.
Таким образом, на границе раздела двух диэлектриков касательные составляющие напряженности электрического поля изменяются непрерывно, а нормальные составляющие - скачкообразно.
Заключение: С учетом того, что напряженность поля в диэлектрике E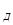 = Е /
= Е / 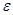 , т. е. в
, т. е. в 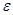 раз меньше, чем в вакууме, ряд формул, описывающих взаимодействие зарядов в диэлектрике, будут иметь другой вид:
раз меньше, чем в вакууме, ряд формул, описывающих взаимодействие зарядов в диэлектрике, будут иметь другой вид:
a) закон Кулона F = 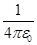
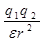 , (11)
, (11)
b) напряженность поля точечного заряда q, окруженного диэлектриком, E=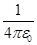
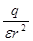 ,(12)
,(12)
c) потенциал поля точечного заряда q, окруженного диэлектриком,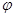 =
=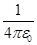
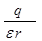 , (13)
, (13)
d) напряженность поля заряженной плоскости, окруженной диэлектриком, E = 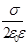 , (14)
, (14)
e) напряженность поля между двумя разноименно заряженными пластинами, Е=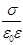 , (15)
, (15)
f) для заряженного цилиндра , окруженного диэлектриком, Е = 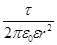 , при r
, при r 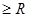 (16)
(16)
g) для заряженного шара, окруженного диэлектриком, E = 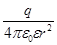 , при r
, при r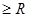 (17)
(17)
и т.д., всюду вместо 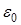 пишется
пишется 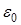
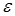 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Поляризация электронная, ориентационная и ионная. Вектор поляризованности | | | Лекция 5. Проводники в электростатическом поле |
Дата добавления: 2014-03-11; просмотров: 975; Нарушение авторских прав

Мы поможем в написании ваших работ!