
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Расчет теплообменных аппаратов
10.2.1. Уравнение теплового баланса. Уравнение баланса массы.
Будем рассматривать аппараты с двумя теплоносителями. Нижние индексы «1» и «2» будут характеризовать параметры горячего и холодного теплоносителей. Верхний индекс «один штрих» будет соответствовать условиям на входе, а «два штриха» - на выходе.
Рассматривая контрольный объем, граничная поверхность которого совпадает с граничной поверхностью теплообменного аппарата, на основании первого закона термодинамики можно записать:
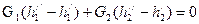 , (10.1)
, (10.1)
Где 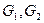 -массовые расходы теплоносителей, кг/с;
-массовые расходы теплоносителей, кг/с; 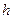 - удельная энтальпиякДж/кг.
- удельная энтальпиякДж/кг.
Уравнение (10.1) представляет собой уравнение теплового баланса. Оно справедливо в случае стационарного режима работы аппарата и в том случае, если можно пренебречь потерями теплоты в окружающую среду и изменением кинетической энергии теплоносителей.
Количество теплоты, передаваемое через единицу времени через поверхность теплообмена от горячего теплоносителя к холодному (тепловая мощность аппарата), равно изменению энтальпии теплоносителей, т.е.
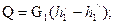
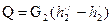 (10.2)
(10.2)
Если 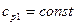 и
и 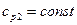 , то вместо (10.2) получим
, то вместо (10.2) получим
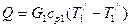
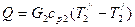 (10.3)
(10.3)
где 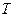 - средняя массовая температура.
- средняя массовая температура.
Для удобства примем: 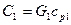 и
и 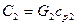 . Величины
. Величины 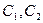 иногда называют водяными эквивалентами.
иногда называют водяными эквивалентами.
Если в аппарате происходит массообмен между теплоносителями, то согласно закону сохранения массы 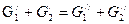 (10.4)
(10.4)
Соотношение 10.4 является уравнением баланса массы теплоносителя. Оно справедливо и в том случае, если в аппарате происходят химические реакции. следует отметить, что при наличии массообмена 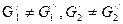 , но справедливо равенство
, но справедливо равенство 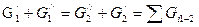 , где
, где 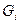 - масса
- масса 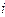 -го компонента, перешедшая в единицу времени из первого теплоносителя во второй (через межфазную поверхность).
-го компонента, перешедшая в единицу времени из первого теплоносителя во второй (через межфазную поверхность).
Уравнение баланса массы для первого и второго теплоносителя
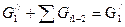 ;
;
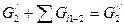 (10.5)
(10.5)
Пусть 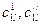 - массовые концентрации
- массовые концентрации 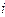 -го компонента в первом теплоносителесоответственно на входе и выходе аппарата, а
-го компонента в первом теплоносителесоответственно на входе и выходе аппарата, а 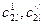 - то же , но для второго теплоносителя. Тогда уравнение баланса массы будет иметь вид:
- то же , но для второго теплоносителя. Тогда уравнение баланса массы будет иметь вид:
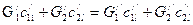 ,
,
Выражение справедливо при отсутствии химических реакций.
10.2.2 Средний температурный напор.
На рис. 10.10 показана расчетная схема к выводу формулы усредненного по поверхности температурного напора для прямотока.
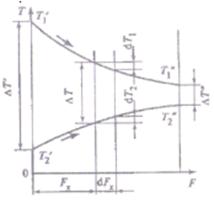
Рис. 10.10
Выделим на расстоянии 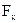 элемент поверхности
элемент поверхности 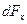 . Запишем для него уравнение теплопередачи
. Запишем для него уравнение теплопередачи 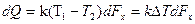 (10.6)
(10.6)
и уравнение теплового баланса 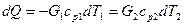 (10.7)
(10.7)
где 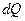 - количество теплоты, передаваемое от горячего теплоносителя холодному в единицу времени через элемент
- количество теплоты, передаваемое от горячего теплоносителя холодному в единицу времени через элемент 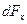 .
.
Из (10.7) следует
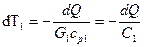 ;
;
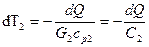

Тогда изменение температурного напора
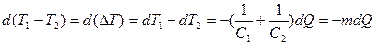 (10.8)
(10.8)
где 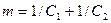 .
.
Подставляя в (10.8) значения 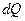 из (10.6) получим
из (10.6) получим 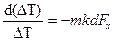 (10.9)
(10.9)
Принимаем упрощения, что вдоль поверхности теплообмена 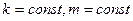 и интегрируя (10.9) получаем
и интегрируя (10.9) получаем
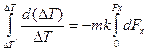
Откуда
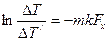 (10.10)
(10.10)
или
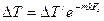 (10.11)
(10.11)
Из (10.11) видно, что вдоль поверхности теплообмена 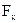 температурный напор уменьшается по экспоненциальному закону.
температурный напор уменьшается по экспоненциальному закону.
Усредненный температурный напор
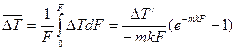 (10.12)
(10.12)
При подстановки получим 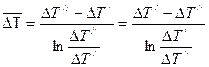 , или
, или
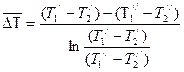 (10.12)
(10.12)
где 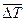 - среднелогарифмический температурный напор.
- среднелогарифмический температурный напор.
Для противотока уравнение (10.8) имеет вид
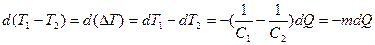 ,
,
где 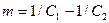 .
.
При этом формула (10.11) сохраняет свой вид, а для среднелогарифмического температурного напора будем иметь
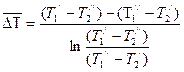 (10.13)
(10.13)
Если 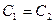 , то в случае противотока
, то в случае противотока 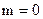 , то
, то 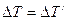 , т.е. средний температурный напор постоянен вдоль поверхности теплообмена.
, т.е. средний температурный напор постоянен вдоль поверхности теплообмена.
Формулы (10.12) и (10.13) можно свести в одну, если независимо от направления движения теплоносителя и конца теплообменника через 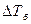 обозначить большую разность температур, а через
обозначить большую разность температур, а через 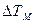 - меньшую, то
- меньшую, то
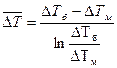
В ряде случаев температуры теплоносителей вдоль поверхности нагрева изменяются незначительно. Тогда средний температурный напор можно вычислить как среднегеометрическое
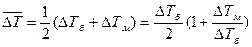
Среднеарифметический температурный напор больше среднегеометрического. Однако, при 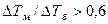 они отличаются меньше чем на 3%, что допустимо в приближенных технических расчетах.
они отличаются меньше чем на 3%, что допустимо в приближенных технических расчетах.
Для сложных схем температурный напор можно выразить как среднелогарифмический температурный напор для противотока 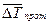 , соответствующий наиболее эффективному теплопереносу. Умноженному на поправочный коэффициент
, соответствующий наиболее эффективному теплопереносу. Умноженному на поправочный коэффициент 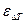 , являющийся функцией параметров
, являющийся функцией параметров 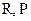 , т.е.
, т.е.
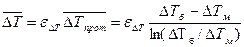 ,
,
где , 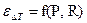 , здесь
, здесь
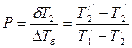 ;
;
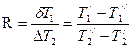
Аналитическое выражение 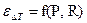 для разных схем движения теплоносителей довольно сложные. Поэтому на практике для нахождения
для разных схем движения теплоносителей довольно сложные. Поэтому на практике для нахождения 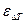 используют график
используют график 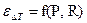 , при этом
, при этом 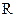 берется в качестве параметра. На рис. 10.11 изображен график
берется в качестве параметра. На рис. 10.11 изображен график 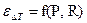 для теплообменника.
для теплообменника.
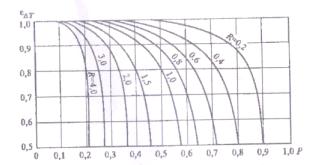
Рис. 10.11
10.2.3 Уравнение теплопередачи.
Для элемента поверхности теплообмена площадью 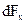 уравнение теплопередачи имеет вид
уравнение теплопередачи имеет вид 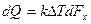 , где
, где 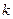 коэффициент теплопередачи;
коэффициент теплопередачи; 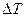 - местный температурный напор.
- местный температурный напор.
Тепловая мощность теплообменника 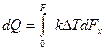 .
.
Коэффициент теплопередачи в случае плоской стенки представляет собой величину, обратную сумме термических сопротивлений:
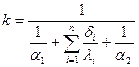
Как и коэффициент передачи, так и температурный напор изменяется вдоль поверхности теплообмена. В простейшем случае (при относительно малом изменении 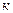 ) можно принять
) можно принять 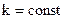 .
.
Тогда уравнение теплопередачи имеет вид
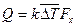 , (*)
, (*)
где 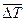 - средний интегральный температурный напор
- средний интегральный температурный напор 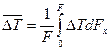 .
.
Для прямо или противоточной схемы движения теплоносителей 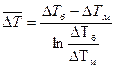 .
.
Если коэффициент теплопередачи сильно изменяется вдоль поверхности теплообмена и к тому же зависит от разности температур 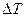 , уравнение (*) теряет смысл. В ряде случаев значение коэффициента зависит от температуры стенки. тогда для расчета площади поверхности теплообмена необходимо использовать поинтервальный метод расчета ( т.е. разбивать всю искомую поверхность на достаточно большое число участков) или прибегать к методу «шаг за шагом».
, уравнение (*) теряет смысл. В ряде случаев значение коэффициента зависит от температуры стенки. тогда для расчета площади поверхности теплообмена необходимо использовать поинтервальный метод расчета ( т.е. разбивать всю искомую поверхность на достаточно большое число участков) или прибегать к методу «шаг за шагом».
Уравнение (*) можно также представить в виде
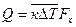 , (**)
, (**)
где 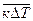 - среднее интегральное значение
- среднее интегральное значение 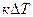 .
.
Из (**) видно, что от значения коэффициента теплопередачи зависит площадь поверхности теплообмена. Чем больше этот коэффициент, тем меньше площадь поверхности теплообмена. Уменьшая термическое сопротивление процессу теплопередачи, можно уменьшить площадь, т.е. сократить габаритные размеры теплообменника. Поскольку с увеличением скорости течения теплоносителя коэффициент теплоотдачи возрастает, уменьшение площади проходного сечения теплообменника способствует увеличению значения 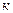 . Однако, всегда надо иметь ввиду, что с увеличением скорости возрастает (причем более резко) гидравлическое сопротивление и увеличиваются затраты мощности на прокачку теплоносителя. Увеличить коэффициент теплоотдачи можно исскуственным путемс помощью методов интенсификации, используя специально изготовленные трубы с шероховатостью или иной поверхностью, применяя закрутку потока и т.п.
. Однако, всегда надо иметь ввиду, что с увеличением скорости возрастает (причем более резко) гидравлическое сопротивление и увеличиваются затраты мощности на прокачку теплоносителя. Увеличить коэффициент теплоотдачи можно исскуственным путемс помощью методов интенсификации, используя специально изготовленные трубы с шероховатостью или иной поверхностью, применяя закрутку потока и т.п.
10.2.4 Проверочный расчет теплообменного аппарата. Сравнение прямотока с противотоком.
Прямоточная схема движения теплоносителей. Температурный напор на выходе из теплообменника 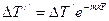 ,
, 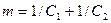 ,
, 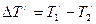 , тогда
, тогда
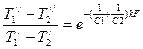 ,
,
Преобразуем: 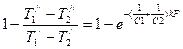 , получим
, получим
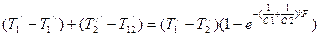 ,
,
Далее учтем 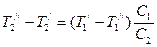 и после простых преобразований получим
и после простых преобразований получим
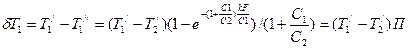 (*)
(*)
Уравнение (*), показывает, что изменение температуры горячего теплоносителя равно некоторой доле ПР располагаемого температурного напора 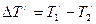 . Эта доля зависит от двух безразмерных параметров
. Эта доля зависит от двух безразмерных параметров 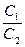 и
и 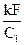 :
:
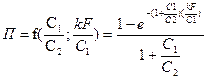 (**)
(**)
Для холодного теплоносителя:
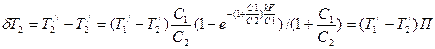 (***)
(***)
Из (*) и (***) определяем конечные температуры теплоносителей
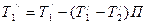 ;
;
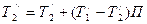 .
.
Тепловой поток 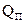 передаваемый через поверхность теплообмена при прямотоке определяется из (*)
передаваемый через поверхность теплообмена при прямотоке определяется из (*)
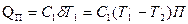
Противоточная схема движения теплоносителей. Для противотока расчетные формулы выводятся так же и имеют следующий вид:
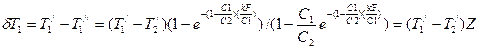 ;
;
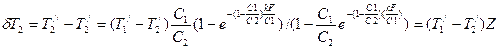 ;
;
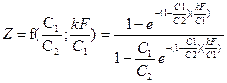 ;
;
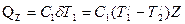 ;
;
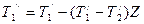 ;
;
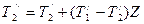 .
.
Сравнение прямотока с противотоком. Если разделить количество теплоты при прямотоке, на количество теплоты, переданное при противотоке при почих равных условиях, то получим новую безразмерную функцию от 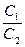 и
и 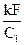 рис. 10.1, показывающую, какая доля теплоты противотока передается при прямоточной схеме движения теплоносителей:
рис. 10.1, показывающую, какая доля теплоты противотока передается при прямоточной схеме движения теплоносителей: 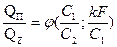
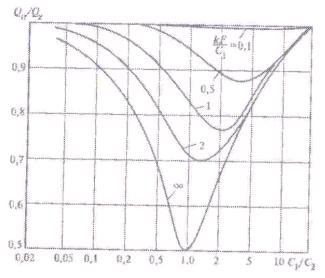
Рис. 10.1. Сравнение прямотока с противотоком
Как следует из рис. 10.1, прямоточные и противоточные схемы могут быть равноценны только при очень больших и очень маых значениях 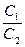 (
(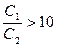 и
и 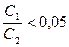 ) или очень малых значениях
) или очень малых значениях 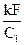 . Первое условие соответствует случаю, когда изменение температуры одного теплоносителя мало по сравнению с изменением температуры другого. Второе условие равнозначно случаю, когда средний температурный напор значительно превышает изменение температуры теплоносителей, так как
. Первое условие соответствует случаю, когда изменение температуры одного теплоносителя мало по сравнению с изменением температуры другого. Второе условие равнозначно случаю, когда средний температурный напор значительно превышает изменение температуры теплоносителей, так как 
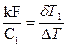 либо
либо 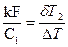 . Во всех остальных случаях при прочих равных условиях противоток предпочтителен по сравнению с прямотоком. Однако, надо иметь ввиду, что температурные условия для конструктивных материалов при противотоке более жесткие, чем при прямотоке.
. Во всех остальных случаях при прочих равных условиях противоток предпочтителен по сравнению с прямотоком. Однако, надо иметь ввиду, что температурные условия для конструктивных материалов при противотоке более жесткие, чем при прямотоке.
10.2.5 Гидравлический расчет аппаратов.
Целью гидравлического расчета является определение потерь давления при прохождении теплоносителя через теплообменный или тепломассообменный аппарат. Потери давления в первую очередь обусловлены сопротивлением трения, возникающим из-за вязкоти жидкости. Это сопротивление существенно зависит от скорости теплоносителя. В первом приближении можно принять, что при турбулентном течении жидкости в трубе перепад давлений 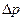 на ее концах пропорционален квадрату скорости. От
на ее концах пропорционален квадрату скорости. От 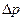 зависит значение мощности, необходимой для перемещения жидкости, так как
зависит значение мощности, необходимой для перемещения жидкости, так как 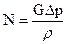 , где
, где 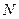 - мощность, Вт;
- мощность, Вт; 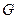 - массовый расход жидкости, кг/с;
- массовый расход жидкости, кг/с; 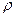 - плотность жидкости, кг/м3 ;
- плотность жидкости, кг/м3 ; 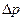 - гидравлическое сопротивление, Па.
- гидравлическое сопротивление, Па.
Зная значение 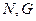 можно подобрать насос или вентилятор, который будет обеспечивать прокачку теплоносителя через аппарат. При этом надо учитывать также КПД насоса и вентилятора.
можно подобрать насос или вентилятор, который будет обеспечивать прокачку теплоносителя через аппарат. При этом надо учитывать также КПД насоса и вентилятора.
Так как расход 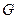 пропорционален скорости, а гидравлическое сопротивление
пропорционален скорости, а гидравлическое сопротивление 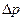 - приблизительно скорости в квадрате (для турбулентного режима течения, который наиболее часто встречается на практике), то в первом приближении мощность
- приблизительно скорости в квадрате (для турбулентного режима течения, который наиболее часто встречается на практике), то в первом приближении мощность 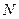 пропорциональна скорости в кубе. В связи с этим расчет гидравлического сопротивления и выбор оптимальной скорости теплоносителя имеет большое значение.
пропорциональна скорости в кубе. В связи с этим расчет гидравлического сопротивления и выбор оптимальной скорости теплоносителя имеет большое значение.
Полное гидравлическое сопротивление складываается из трех частей:
- сопротивление трения. Которое для течения в каналах определяется 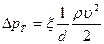 , где
, где 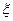 - коэффициент сопротивления, зависящий от числа Рейнольдса,
- коэффициент сопротивления, зависящий от числа Рейнольдса, 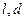 - длина и диаметр трубы,
- длина и диаметр трубы, 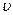 - скорость теплоносителя;
- скорость теплоносителя;
- состовляющая потерь давления обусловлена местными сопротивлениями (на входе в трубу или межтрубное пространство, повороте и др.). определяется по формуле: 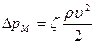 , где
, где 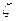 - местный коэффициент сопротивления. Для конкретных условийзначение
- местный коэффициент сопротивления. Для конкретных условийзначение 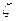 выбирается из таблиц. При наличии нескольких местных сопротивлений потери давления от каждого из сопротивлений складываются;
выбирается из таблиц. При наличии нескольких местных сопротивлений потери давления от каждого из сопротивлений складываются;
- составляющая гидравлических потерь связана с ускорением потока: 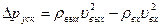 , где индексы входа и выходы соответсвуют условиям на входе и выходе из теплообменного аппарата.
, где индексы входа и выходы соответсвуют условиям на входе и выходе из теплообменного аппарата.
Если аппарат сообщается с атмосферой, при расчете 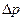 следует учитывать гидростатические потери. Для замкнутых систем они равны нулю.
следует учитывать гидростатические потери. Для замкнутых систем они равны нулю.
При ламинарном стабилизированном течении в трубе 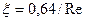 .
.
При турбулентном стабилизированном течении в технически гладкой трубе 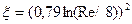
Если высота шероховатости стенки трубы 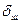 соизмерима с толщиной вязкого подслоя, то оказывается, что гидравлическое сопротивление этой трубы больше, чем гладкой. При этом
соизмерима с толщиной вязкого подслоя, то оказывается, что гидравлическое сопротивление этой трубы больше, чем гладкой. При этом
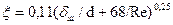 , если
, если 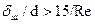 и
и 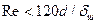 ;
;
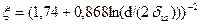 , если
, если 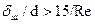 и
и 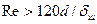 .
.
При неизотермическом течении в формулы следует вводить поправку.
Гидравлическое сопротивление при поперечном обтекании пучка труб 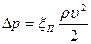 , где
, где 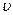 - скорость в узком сечении пучка,
- скорость в узком сечении пучка, 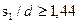 и
и 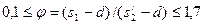 , то
, то 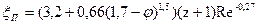 ;
;
Расположение труб шахматное: 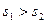 и
и 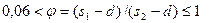
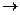
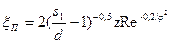 ;
;
Расположение труб коридорное: 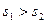 и
и 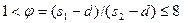
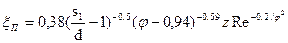 .
.
где 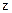 - число рядов;
- число рядов; 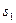 - шаг труб в поперечном направлении;
- шаг труб в поперечном направлении; 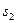 - шаг труб в направлении потока;
- шаг труб в направлении потока; 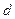 - наружный диаметр трубы;
- наружный диаметр трубы; 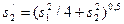 - диагональный шагш труб.
- диагональный шагш труб.
| <== предыдущая страница | | | следующая страница ==> |
| Аппараты смешивающего типа | | | Тепловой расчет регенеративных теплообменников |
Дата добавления: 2014-03-11; просмотров: 1163; Нарушение авторских прав

Мы поможем в написании ваших работ!