Тезисы к лекции. Модели дискретных каналов связи

Модели дискретных каналов связи

Дискретный канал всегда содержит внутри непрерывный канал. Преобразование непрерывного канала в дискретный производит модем. Поэтому в принципе можно получить математическую модель дискретного канала из модели непрерывного канала при заданном модеме. Образно говоря, модем, осуществляющий переход от непрерывного канала в поток ошибок. Наиболее важные и достаточно простые модели дискретных каналов следующие.

Постоянный симметричный канал без памяти определяется как дискретный канал, в котором каждый переданный кодовый символ может быть принят ошибочно с фиксированной вероятностью р и правильно с вероятностью 1-р, причём в случае ошибки вместо переданного символа может быть с равной вероятностью принят любой другой символ. Термин “без памяти” означает, что вероятность ошибочного приёма символа не зависит от предистории, т.е. от того, какие символы передавались до него и как они были приняты. Вероятности переходов в двоичном симметричном канале схематически можно представить в виде графа (рис.3.1).

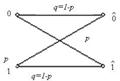
Рисунок 3.1. Переходные вероятности в двоичном симметричном канале

Постоянный симметричный канал без памяти со стиранием отличается от предыдущего канала тем, что алфавит на выходе канала содержит дополнительный (m+1)-й символ, который часто обозначают знаком “?”. Этот символ появляется тогда, когда демодулятор не может надёжно опознать переданный символ. Вероятность такого отказа от решения или стирания символа p_c в данной модели постоянна и не зависит от передаваемого символа. За счёт введения стирания удаётся значительно снизить вероятность ошибки, иногда её даже считают равной нулю. На рис.3.2 показаны вероятности переходов в такой модели.

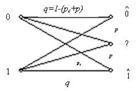
Рисунок 3.2. Переходные вероятности в двоичном симметричном канале со стиранием

Несимметричный канал без памяти характеризуется тем, что ошибки в нём возникают независимо друг от друга, однако вероятности ошибок зависят от того, какой символ передаётся. Так, в двоичном несимметричном канале вероятность приёма символа 1 при передаче символа 0 не равна вероятности приёма 0 при передаче 1.

Простейшей моделью двоичного канала с памятью является марковская модель, определяемая матрицей переходных вероятностей:

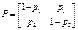(3.1)

где р₁—условная вероятность принять (i+1)-й символ ошибочно, если предыдущий принят правильно; (1-р₁)-условная вероятность принять (i+1)-й символ правильно, если предыдущий символ принят правильно; р₂- условная вероятность принять (i+1)-й символ ошибочно, если предыдущий принят ошибочно; (1-р₂)-условная вероятность принять (i+1)-й символ правильно, если предыдущий символ принят ошибочно.

Безусловная (средняя) вероятность ошибки p в таком канале должна удовлетворять уравнению:

р=Р₂р+З₁(1-р)

Откуда

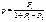(3.2)

Другой подход к построению математических моделей каналов связан с методом переменных состояния. Важной особенностью этого метода является возможность непосредственного моделирования систем, описываемых уравнениями состояния с помощью аналогового или цифрового вычислительного устройства. Уравнения состояния обычно составляют в виде системы дифференциальных уравнений первого порядка, которую приводят к форме векторного (матричного) дифференциального уравнения первого порядка. Этот метод даёт универсальный подход для моделирования каналов передачи информации систем связи для самых различных сообщений, способов кодирования и модуляции, линий связи с детерминированными и случайными параметрами и аддитивными шумами.

Краевые искажения и дробления.

Под действием различных дестабилизирующих факторов: не идеальность характеристик НКС; действие помех, элементы сигнала могут искажаться по длительности, т. е. появляются краевые искажения и дробления.

Индивидуальные КИ – смещения ЗМ относительно идеального значащего момента

Относительные КИ – это индивидуальные, отнесенное к длительности единичного элемента.

Преобладания – элементы одного знака удлиняются, а другого укорачиваются.

Дробления – это искажения, при которых один элемент преобразуется в несколько более коротких (дробится).

Методы регистрации сигналов.

Процесс определения и запоминания значащей позиции сигнала данных – называется регистрацией.

Метод стробирования – значащая позиция принимаемого элемента определяются на основании анализа знака импульса в середине единичного интервала. Если индивидуальное КИ не превышает 0,5τ, то элемент регистрируются правильно.

Исправляющая способность – это величина, на которую допускаются смещения ЗМ, не вызывающее неправильный прием элемента.

Интегральный метод регистрации - решение о виде принятого элемента выносится на основании анализа напряжения на всем единичном интервале.

В идеальном случае (если единичный. элемент не искажен), то U_вых = 1; решением о «1» принимается при U_вых >= 0,5; решением о «0» принимается при U_вых < 0,5.

Дата добавления: 2014-03-22; просмотров: 387; Нарушение авторских прав

Мы поможем в написании ваших работ!