
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Уточнение некоторых фундаментальных геодезических постоянных
При решении многих научных задач методы космической геодезии имеют существенные преимущества по сравнению с традиционными.
Это связано с тем, что традиционные геодезические построения создаются на отдельных территориях и образуют референцные геодезические системы. В этом случае расположение референц-эллипсоидов относительно друг друга и центра масс Земли нельзя установить при помощи только триангуляции и полигонометрии. То есть нельзя осуществить геодезическую связь всех материков в единую мировую геодезическую систему.
Такую связь можно осуществить лишь только методом космической геодезии. Это связано с тем, что возможности космических методов ограничены из-за сравнительно небольших предельных длин отдельных сторон триангуляции и полигонометрии, которые достигают максимум 400км.
Поэтому одновременно с работами по совершенствованию традиционных геодезических методов, создавались предпосылки для развития космической геодезии. Для этого использовались наблюдения Луны. Однако эти работы не позволили достичь необходимой точности из-за того, Что Луна находится на очень большом расстоянии от Земли ( в среднем 384000км). Поэтому ошибки в регистрации времени наблюдений равные 0,1S приводят к ошибке в положении пункта, равный примерно 100-200км. Указанные обстоятельства привели к тому, что методы, основанные на использовании Луны практически не нашли применения в геодезии.
Исключительно важное значение для развития теории и практики космической геодезии имело предложение финского геодезиста Вяйсяля (1946г.). Он предложил фотографировать с 2х пунктов синхронно какую-либо визирную цель на фоне звездного неба. Например, лампы-вспышки на шарах-зондах, самолетах, аэростатах. В результате оказалось возможным определить направления хорд, соединяющих все пункты наблюдений. Располагая координатами одного из них и хотя бы одним базисом, можно вычислить координаты всех пунктов в системе исходного. Однако до запуска ИСЗ этот метод почти не применялся и только после запуска 4 октября 1957г. первого искусственного спутника начинается бурно развиваться космическая геодезия.
Из большого количества запускаемых на орбиты ИСЗ, особо важное значение для геодезии имеют специальные геодезические ИСЗ, наблюдения на которые позволяют быстро передавать координаты на расстояния в несколько тысяч км и создавать геодезическую сеть в абсолютной системе координат, отнесенной к центру масс Земли, а также определять основные параметры гравитационного поля Земли, причем получают результаты гораздо надежнее, чем традиционными методами.
Кроме того, методы Космической геодезии позволяют использовать результаты наблюдений ИСЗ при изучении дрейфа континентов и движения Земных полюсов, а также при определении фигуры геоида в океанах и при решении проблем картографирования Земли из космоса.
Понятие о геометрическом и динамическом методах космической геодезии.
Методы решения задач космической геодезии обычно подразделяют на геометрические и динамические.
Геометрический метод предусматривает использование ИСЗ как высокой визирной цели ( теорию движения ИСЗ в этом методе используют лишь приближенно для определения эфемерид, необходимых при выполнении наблюдений спутника). При реализации геометрических методов используют синхронные или квазисинхронные наблюдения ИСЗ с нескольких пунктов.
Динамический метод космической геодезии заключается в совместном определении параметров гравитационного поля Земли, координат пунктов наблюдений и элементов орбиты из совокупности измерений, выполненных на пунктах.
В динамическом методе в качестве основы для вывода параметров гравитационного поля Земли и определения координат пунктов в абсолютной системе координат, отнесенной к центру масс Земли, используют теорию движения ИСЗ. (Возмущения орбиты - для гравитационных определений, а элементы орбиты - для получения координат пунктов).
Для обоснования методов использования наблюдений ИСЗ в геодезии, рассмотрим чертеж:
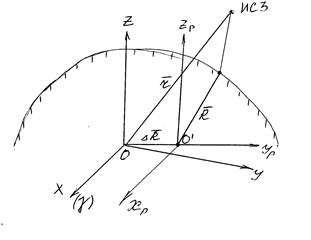 О- центр масс Земли. Начало
О- центр масс Земли. Начало
прямоугольной пространственной
инерциальной системы координат
О’- центр референц-эллипсоида. Начало
прямоугольной пространственной
Гринвичской (референцной)
системы координат
τ- геоцентрический радиус-вектор
ИСЗ в системе координат,
Отнесенной к центру масс Земли.
τ' - топоцентрический радиус-вектор ИСЗ, в системе координат, отнесенной в точку на поверхности Земли.( пункт наблюдений).
R- радиус-вектор пункта Р в системе координат, отнесенной к центру референц-эллипсоида
∆R- вектор, связывающий О’- центр референц-эллипсоида с центром масс Земли О.
Векторы τ, τ', R и ∆R связаны соотношением:

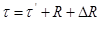 (1)
(1)
Которое является фундаментальным уравнением космической геодезии.
Если по результатам наблюдений ИСЗ решают задачу по определению координат спутника (прямая задача), то используют формулу (1).
Однако в космической геодезии чаще приходиться рассматривать вопрос об определении координат пунктов наблюдений (обратная задача). В этом случае из (1) найдем:
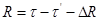 . (2)
. (2)
В космической геодезии обычно используют несколько синхронных наблюдений ИСЗ с двух или нескольких пунктов.
Поэтому, если для некоторого момента на пунктах Р1 и Р2 синхронно определены компоненты топографических векторов τ’1 и τ’2, то получим 2 векторных уравнения:
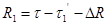
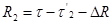 , вычитая найдем
, вычитая найдем
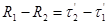 (3)
(3)
Если координаты одного из пунктов заданы, то уравнение (3) дает возможность получить координаты другого пункта в системе исходного. Уравнение (3) применяют в геометрическом методе космической геодезии.
В динамическом методе космической геодезии используют другое уравнение. В котором геоцентрический радиус-вектор ИСЗ является функцией элементов орбиты Еi , параметров ψк гравитационного поля и величины t.
Тогда: 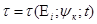 (4)
(4)
Функция (4) имеет очень сложный вид, поэтому считая, что измеренными величинами в динамическом методе являются топоцентрические радиусы-векторы (τ') по (1) получим приближенное уравнение:
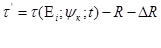 (5)
(5)
Из уравнения (5), полагая безошибочными элементы регистрации времени и не определяя поправки к принятой модели гравитационного поля Земли, после преобразований с учетом того, что для моментов измерений известны элементы орбиты (Ei), получим уравнение упрощенного орбитального метода:
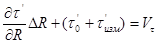 (6)
(6)
Где τ’0 – приближенное значение топоцентрического радиус-вектора ИСЗ;
Vτ - вероятнейшая поправка измеренной величины.
Уравнение (6) позволяет определять лишь координаты пунктов, а элементы орбиты и параметры гравитационного поля предполагаются известными.
В настоящее время по результатам наблюдений ИСЗ решают задачи, применяя как геометрический, так и динамический методы космической геодезии. Например, успехи, достигнутые в решении динамических задач, позволили по параметрам, характеризующим гравитационное поле Земли, судить о свойствах и форме уровенной поверхности; о геофизических свойствах земной коры и мантии Земли.
Геометрические методы позволяют развивать мировую геодезическую сеть, определять параметры общего земного эллипсоида и т.д.
Лекция 2. Основные системы координат, применяемые в космической геодезии. Системы измерения времени.
Для решения многочисленных задач космической геодезии применяют различные системы координат, которые различаются: по форме их задания; по выбору начала координат; по выбору основной плоскости и по ориентации главной оси координат.
В связи с этим в космической геодезии существует следующая классификация координат:
1. По форме: прямоугольные и криволинейные (сферические, сфероидические)
2. По выбору начала координат: геоцентрические (в центре Земли) и топоцентрические (на поверхности Земли)
3. По выбору основной координатной плоскости: экваториальные, горизонтные, орбитальные.
4. По выбору направления оси ОХ: инерциальные (ось ОХ направлена в точку весеннего равноденствия γ)- неподвижные относительно вращающейся Земли. Гринвичские (референцные)- ось ОХ направлена в точку пересечения начального (гринвичского) меридиана и экватора. Системы вращаются вместе с Землей.
5. По положению оси ОZ и точку γ. Ось OZ совпадает с осью вращения Земли. Системы бывают: мгновенные, истинные и средние.
Исходной системой координат, в которой задаются положения станций наблюдений ИСЗ, является геодезическая, определяемая принятым на данной территории референц-эллипсоидом. Положение точек на земной поверхности задается: геодезической широтой В; геодезической долготой L; геодезической высотой Н над эллипсоидом.
Референц-эллипсоид ориентируют так, чтобы его малая ось была параллельна средней оси вращения Земли в некоторою стандартную эпоху to.
Так как космическая геодезия позволяет решать геодезические задачи в масштабе всей Земли, то иногда в качестве исходного целесообразно использовать общий Земной эллипсоид. Центр этого эллипсоила совпадает с центром масс Земли, а малая полуось совпадает со средней осью вращения Земли для выбранной эпохи to (1900, 1960, 1990, 2000 и т.д.).
Размеры общего земного эллипсоида: а=6378140км; α=1:298,257
( Красовского: а=6378245км; α=1:298,3).
Системы измерения времени, используемые в КГ.
В космической геодезии за исходную принята система всемирного времени UТ ( Universal Time), т.е. система среднего солнечного времени на гринвичском меридиане.
Чтобы перейти к системе UT поступают следующим образом: из наблюдений звезд в пункте с известной астрономической долготой λ определяют местное звездное время s, т.е. часовой угол точки весеннего равноденствия (γ) относительно местного астрономического меридиана в момент наблюдений.
Гринвичское звездное время в этот момент равно:
S= s- α, а всемирное: UT= (S-S0)- (S-S0)υ , где S0- звездное время в гринвичскую полночь( по среднему солнечному времени)
υ= 1/366,2422- коэффициент перехода от звездного времени к среднему
Всемирное время, отнесенное к положению мгновенного полюса, мгновенного экватора и мгновенного положения точки весеннего равноденствия, обозначается UT-0.
Всемирное время в системе UT-0 является неравномерным из-за неравномерностей, вызываемых движением полюсов, сезонными изменениями угловой скорости вращения Земли под действием геодезических и метеорологических факторов, вековым замедлением вращения Земли из-за приливного трения в системе Земля-Луна, непериодическими изменениями угловой скорости вращения Земли, в основном из-за влияния Солнечной активности.
В настоящее время созданы службы времени, а так же Международная служба движения полюсов, которые позволяют определять поправку ∆λ к системе UT-0, учитывающую движение мгновенного полюса относительно среднего. При помощи этой поправки образуется система времени UT-1.
UT-1= UT-0+∆λ (1)
Служба времени определяет так же поправку ∆ UT за сезонные вариации угловой скорости вращения Земли. При помощи этой поправки образуется система квазиравномерного времени UT-2:
UT-2= UT-1+∆ UT= UT-0+∆λ +∆ UT (2)
Международное бюро времени регулярно публикует поправки ∆λ и ∆ UT , для того чтобы редуцировать моменты подачи радиосигналов точного времени к системе UT-2. В связи с этим выпускают издания, которые называются: « Циркуляр Бюро времени» и «Бюллетень времени».
Для промежутка времени не больше одного года при решении различных практических задач достаточно пользоваться системой времени UT-2. При больших промежутках времени (больше года) целесообразно пользоваться системой эфемеридного времени ET. Эфемеридное время- равномерно текущее ( теоретическое) время небесной механики.
Переход от всемирного к эфемеридному времени осуществляется по формуле:
ET=UT+∆T, где поправка ∆T определяется из наблюдений Луны путем сравнения ее наблюденных координат с эфемеридными, вычисленными согласно исправленной гравитационной теории движения Луны, разработанной Брауном.
Точность определения поправки ∆T из наблюдений Луны пока невелика- ошибка несколько меньше одной секунды времени.
В настоящее время во многих странах осуществлен переход на систему атомного времени АТ, которая основана на применении высокостабильных атомных и молекулярных эталонов частоты.
Стабильность атомных эталонов такова, что точность определения одной атомной секунды составляет 1s ±10-11 секунд. Для образования системы атомного времени задействовано 10 атомных часов, связанных с Международным Бюро времени. Эти часы находятся в США, Канаде, Японии, ЮАР, Франции, Англии и Швеции.
В настоящее время применяется новая шкала атомного времени АЗ, которая введена с 1 января 1966года и вычисляется как средневзвешенная шкала показаний всех атомных часов, связных с Международным Бюро времени.
В нашей стране принята шкала атомного времени АТ-1, основанная на 2х кварцевых часах, которые регулируются цезиевым эталоном частоты.
Было принято, что в момент 1964г, 1 января 12h :
UT-2=AT-1
Разности Фе-1 и UT-2 публикуются в бюллетени «Эталонное время». В СНГ применяется так же шкала UTC- шкала всемирного согласованного или координированного времени. Ее используют для согласования между собой шкал атомного и всемирного времени ФЕ-1 и UT-2.
Для непрерывного счета времени на больших промежутках применяется предложенная еще в XVI веке, так называемая юлианская система (Юлианский период), начало которой приходится на средний гринвичскаий полдень 1 января 4713г. До н.э., после чего ведется непрерывный счет суток. Юлианский год содержит 365,25 эфемеридных суток.
Лекция 3. Теория движения искусственных спутников Земли (ИСЗ). Невозмущенное движение ИСЗ.
Если бы Земля была строго сферической с равномерным распределением плотности, то ее гравитационный потенциал совпадал бы с потенциалом материальной точки, масса которой равна массе Земли. В этом случае спутник двигался бы по законам Кеплера:
1й закон Кеплера: Орбитой спутника является кривая 2ого порядка (окружность, эллипс, парабола), в одном из фокусов которой находится центр масс притягивающего тела.
Спутники, летающие вокруг Земли, имеют эллиптическую орбиту. Эллипс- это геометрическое место точек, сумма расстояний от каждой из которых до двух точек, называемых фокусами, является величиной постоянной, равной 2а, где а- большая полуось эллипса.
PF1+PF2 = 2a
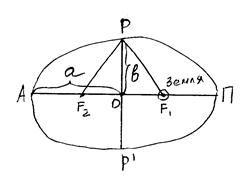
F1 и F2 - фокусы эллипса
АП- линия АПСИД
А-апогей (спутник имеет
наибольшую высоту над землей)
П- перигей (спутник имеет
наименьшую высоту над Землей).
2й закон Кеплера: Радиус-вектор спутника за равные промежутки времени описывает равные площади. Если t1= t2, то S1= S2. Согласно чертежа: путь за время t1 больше, чем время t2, поэтому скорость ИСЗ вблизи перигея больше, чем вблизи апогея.
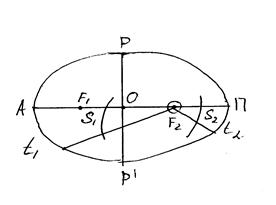
Фигура, описываемая радиус-вектором спутника-это сектор. Поэтому согласно 2ому закону Кеплера: секториальная скорость ИСЗ есть величина постоянная.
3й закон Кеплера: Отношение квадрата периода обращения спутника к кубу большой полуоси его орбиты является величиной постоянной:
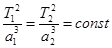
Если предположить, что спутник движется по орбите по законам Кеплера, то такое движение называется невозмущенным.
В действительности движение спутника по орбите очень сложное. Действуют различные возмущающие силы. Движение ИСЗ в этом случае называетсявозмущенным.
Невозмущенное движение ИСЗ.
Будем считать, что спутник является материальной точкой с массой m. Если движение спутника невозмущенное, то Землю так же принимаем за материальную точку с массой M. С учетом того, что m « М, можно считать что спутник Землю практически не притягивает, т.е. имеет «нулевую массу».
Для вывода дифференциальных уравнений невозмущенного движения ИСЗ выбирем инерциальную систему координат (т.е. неподвижную относительно вращающейся Земли).
Ось ОХ направлена в точку весеннего равноденствия (γ) на какую-либо эпоху t0 ( 1960, 1990, 2000); Ось OZ направлена (совпадает) по средней оси вращения Земли, относительно той же эпохи t0 ; ось ОУ дополняет систему до правой и лежит в плоскости среднего экватора на ту же эпоху.
Если учитывать действие других сил, кроме взаимодействия Земли и спутника, то вывод дифференциальных уравнений невозмущенного движения ИСЗ, сводится к решению так называемой задачи двух тел.
Тогда, пренебрегая действием спутника на Землю, рассмотрим ускорение ω, которая задает Земля спутнику вследствие закона тяготения.
По второму закону Ньютона:
F=m*ω,
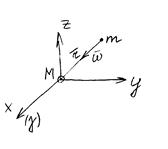
где сила F в соответствии
с законом тяготения:
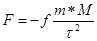
f- постоянная тяготения
τ- геоцентрический радиус-вектор ИСЗ.
Приравнивая найдем:
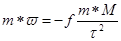 ;
; 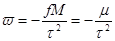 (1)
(1)
Где f*M=μ- гравитационный параметр
В уравнении (1) ω- ускорение, т.е. вторая производная от пути по времени, поэтому 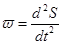 ;
;
Рассмотрим ускорения вдоль координатных осей:
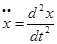 ;
; 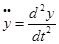 ;
; 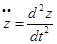
Что бы найти эти величины, нужно правую часть уравнения (1) умножить на направляющие косинусы (α- по оси ОХ, β- по оси ОУ, γ- по оси ОZ): 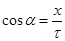 ;
; 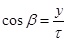 ;
; 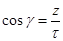 ; тогда
; тогда
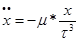
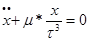
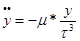
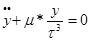 (2)
(2)
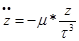
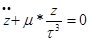
Формулы (2)-это дифференциальные уравнения невозмущенного движения ИСЗ.
Лекция 4. Интегрирование дифференциальных уравнений невозмущенных движений ИСЗ. Интеграл площадей.
Система дифференциальных уравнений (2) является системой 6ого порядка, поэтому должны существовать 6 независимых интегралов, полностью определяющих движение спутника, т.е. вид и форму орбиты; ее положение в пространстве и закон движения по ней. Каждый интеграл содержит одну произвольную постоянную, поэтому 6 произвольных постоянных полностью определяют невозмущенное движение ИСЗ.
Интегрируя (2) методом разделения переменных, получим:
Три интеграла площадей; интеграл энергии; интеграл орбиты и динамический интеграл.
Интеграл площадей.
Запишем дифференциальные уравнения невозмущенного движения: Умножим по схеме и сложим, тогда:
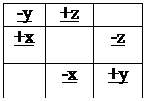
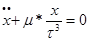
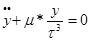
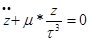
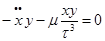
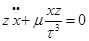
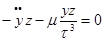
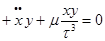
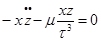
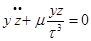
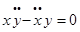
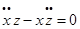
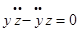
В каждом из полученных уравнений заменим одну производную через дифференциал, тогда получим:
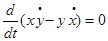 интегрируя эту систему найдем:
интегрируя эту систему найдем:
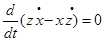
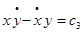 умножим по схеме, сложим
умножим по схеме, сложим
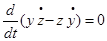
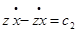 и получим:
и получим:
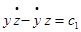
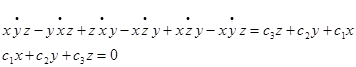 (3)
(3)
Это значит, что невозмущенная орбита ИСЗ лежит в плоскости, проходящей через центр масс Земли и называется орбитальной плоскостью.
Если в орбитальной плоскости выбрать произвольную систему плоских прямоугольных координат ξ и η, то по аналогам с пространственной системой по осям ξ и η, получим:
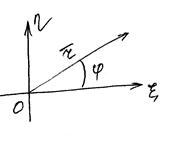
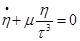 ξ умножим по схеме, сложим
ξ умножим по схеме, сложим
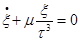 -η и найдем:
-η и найдем:
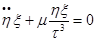
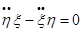 Заменим одну производную через
Заменим одну производную через
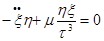 дифференциал, тогда:
дифференциал, тогда:
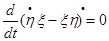 после интегрирования найдем:
после интегрирования найдем:
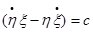 (4)
(4)
В данной плоской системе координат рассмотрим возможность определения 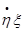 и
и 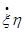 через полярные координаты
через полярные координаты 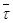 и φ, тогда
и φ, тогда 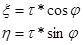 ,
,
Дифференцируя, найдем: 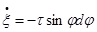 ;
; 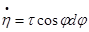 (5)
(5)
Подставляя (5) в (4) получим:

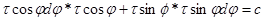 Откуда:
Откуда:
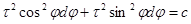 или
или
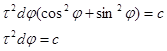 (6)
(6)
Если в этом уравнении взять производную по времени, то получим удвоенную секториальную скорость, т.е. удвоенную площадь, описываемую радиус-вектором τ в единицу времени.
Таким образом, секториальная скорость есть величина постоянная и тем самым строго доказан второй закон Кеплера. Поэтому первые 3 интеграла называются интегралами площадей.
Лекция 5. Элементы орбиты ИСЗ.
При решении практических задач, связанных с использованием ИСЗ, требуется знать положение спутника в пространстве в произвольный момент времени. Для этого, из решения 3х дифференциальных уравнений второго порядка, необходимо найти x,y,z-искомые координаты спутника, которые выражаются функциями от независимого переменного t и 6ти произвольных постоянных (параметров орбиты).
В связи с этим, рассмотрим движение спутника по эллиптической орбите, т.е. установим 6 параметров, из которых 5 определяют пространственное положение орбиты, а 6ой определяет мгновенное положение ИСЗ в пространстве и является функцией времени.
Для этого построим эллиптическую орбиту так, чтобы один из фокусов эллипса совпадал с точкой О (центр масс Земли).
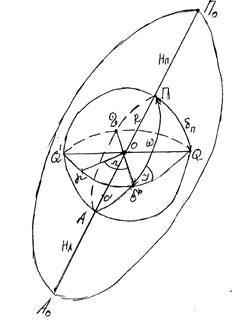
R-радиус сферы (ср.радиус Земли)
О’- центр эллиптической орбиты
П0-перигей, А0-апогей
П- перицентр (проекция П0 на сферу),А-Апоцентр
QQ’-экватор,
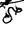 -Восходящий узел орбиты
-Восходящий узел орбиты
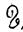 -Нисходящий узел орбиты
-Нисходящий узел орбиты
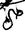
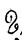 - Линия узлов
- Линия узлов
АП-линия АПСИД, OO’=c=a-ea=a(1-e)
Элементы орбиты:
1. Наклонение орбиты J-угол между плоскостью орбиты и плоскостью экватора;
2. Долгота восходящего узла- угол в плоскости экватора от направления в точку весеннего равноденствия (γ ) до линии узлов.
Эти 2 параметра определяют положение орбиты ИСЗ в пространстве.
3. Большая полуось а орбиты- определяет размер орбиты.
4. Эксцентриситет е орбиты – определяет форму орбиты
5. Склонение перицентра δп (дуга сферы ПQ) или аргумент перигея ω (угол в плоскости орбиты от линии узлов до линии АПСИД). Параметр δп (ω) определяет расположение (ориентирование) эллипса в плоскости орбиты.
6. Момент прохождения ИСЗ через перигей или узел орбиты- t0
Из чертежа следует:
ОП0=R+ Hп =a-c=a-ae=a(1-e)
OA0= R+Ha= a+c=a+ae=a(1+e), откуда
Hп=a(1-e)-R
Ha=a(1+e)-R (1)
Если в системе (1) сложить правые и левые части, то получим:
Ha + Hп=2а-2R; 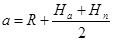 (2)
(2)
Если в системе (1) не сложить, а вычесть, то найдем:
Ha + Hп=2ае; 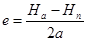 (3)
(3)
Лекция 6. Уравнение движения ИСЗ в плоскости орбиты. Уравнение Кеплера.
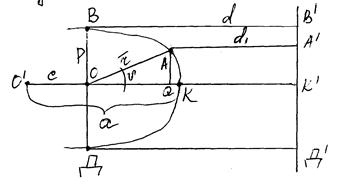
О- начало полярной системы координат
с фокусом эллиптической орбиты ИСЗ
Прямая В’Д’- директриса
Известно, что отношение расстояния
от любой точки эллипса до фокуса
и до директрисы, является величиной
постоянной, численно равной эксцентриситету.
Поэтому:
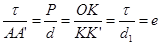 где Р- фокальный параметр орбиты ИСЗ
где Р- фокальный параметр орбиты ИСЗ
Из чертежа: 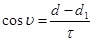 Где υ- истинная аномалия- угол между радиус-вектором ИСЗ и линий АПСИД.
Где υ- истинная аномалия- угол между радиус-вектором ИСЗ и линий АПСИД.
Тогда, с учетом того, что 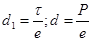 , найдем:
, найдем:
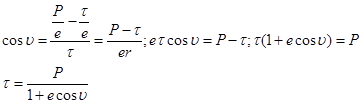
Так как
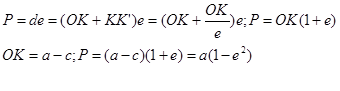 т.к. с=ae. Тогда вместо (1) получим:
т.к. с=ae. Тогда вместо (1) получим:
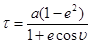 (2)
(2)
Полученное уравнение связывает полярные координаты точек орбиты (τ, υ) с ее геометрическими параметрами (a, e). Однако это уравнение не отражает динамики движения спутника по орбите. Такую связь даст уравнение Кеплера, которое связывает полярные координаты точек орбиты со временем, через некоторые вспомогательные параметры.
Вывод уравнения Кеплера
Согласно 2ого закона Кеплера спутник движется по орбите неравномерно (быстрее у перигея и медленнее у апогея). Такая нелинейная зависимость координат ИСЗ (τ, υ) от времени неудобна для расчетов, поэтому при анализе движения ИСЗ, вводят условные параметры, являющиеся линейной функцией времени.
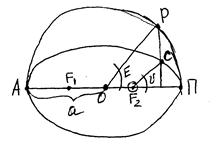
На рис. эллиптическая орбита ИСЗ, по которой
спутник С движется неравномерно. Для введения
условных параметров заменим неравномерное
движение спутника равномерным, происходящим
по круговой орбите с радиусом равным большой полуоси а.
1й условный параметр: это М- средняя аномалия, т.е. дуга окружности, которую описал бы спутник, после прохождения через перигей, если бы он двигался равномерно по круговой орбите, совершая полный оборот за свой фактический период обращения по эллиптической орбите.
2й условный параметр: это υ- истинная аномалия, т.е. угол между радиус-вектором ИСЗ (τ) и линией АПСИД (АП).
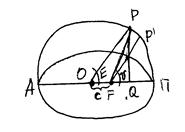
3й условный параметр: Это Е- эксцентрическая аномалия, т.е. угол, который получим следующим образом: через спутник С проводим перпендикуляр к большой оси (АП) эллиптической орбиты и продолжаем его до пересечения с окружностью. Получим точку Р, которую соединяем с центром (О) орбиты. Тогда угол РОП=Е.
Обозначая период обращения спутника через Т, можно написать пропорцию:
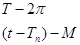 отсюда
отсюда 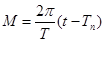 где Тп – момент прохождения ИСЗ через перигей. t- момент прохождения спутником произвольной точки орбиты.
где Тп – момент прохождения ИСЗ через перигей. t- момент прохождения спутником произвольной точки орбиты.
Согласно определению средней аномалии имеем:
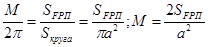 (3)
(3)
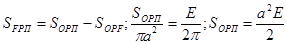 (4)
(4)
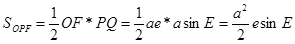 (5)
(5)
С учетом (2) и (3) найдем SFPП:
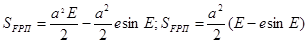 (6)
(6)
Подставляя (4) в (1) получим:
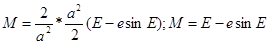 (7)
(7)
Зависимость (7) называется уравнением Кеплера.
Лекция 7. Динамический интеграл. Интеграл энергии.
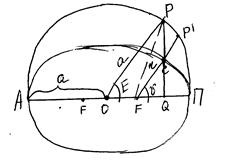 Этот интеграл устанавливает связь между υ и Е.
Этот интеграл устанавливает связь между υ и Е.
Из чертежа: OQ=OF+FQ; (8)
OF=c=ae
Из треуг-ка OPQ OQ=a*cosE
Из треуг-ка FCQ FQ=τ*cosυ,
Тогда вместо (8) найдем
a*cosE=ae+τcosυ;
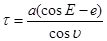 (9)
(9)
Приравнивая правые части уравнений (9) и (2), получим:
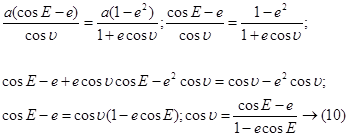
Подставим (10) в (9), найдем:
τ=a(1-ecosE) (11)
Используя известную из тригонометрии формулу, запишем:
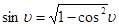 (12)
(12)
Подставим в (12) вместо cosυ его значение из (10), тогда:
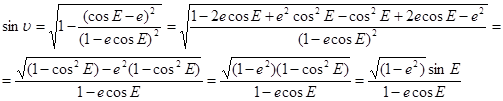 (13)
(13)
Из тригонометрии известно, что 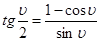 (14)
(14)
С учетом (10) и (13), вместо (14) запишем:
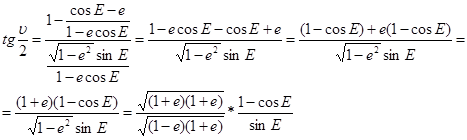
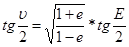 (15)
(15)
Полученное уравнение называется динамический интеграл.
Интеграл энергии.
Запишем, полученные ранее, дифференциальные уравненя невозмущенного движения ИСЗ:
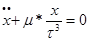
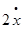 умножим по схеме и сложим. Получим:
умножим по схеме и сложим. Получим:
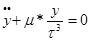
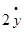
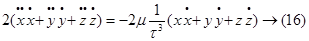
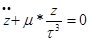
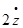 Так как
Так как 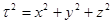 , то дифференцируя
, то дифференцируя
это уравнение и подставляя в (16), получим уравнение эквивалентное (16):

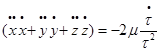 В этом уравнении заменим производную через дифференциал:
В этом уравнении заменим производную через дифференциал:
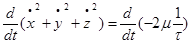 интегрируя, найдем:
интегрируя, найдем:

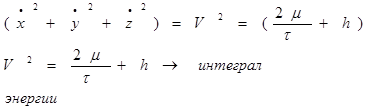 (17)
(17)
Где V- орбитальная скорость ИСЗ, h- постоянная энергии.
С учетом того, что 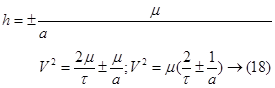 получим вместо (17)
получим вместо (17)
«плюс» соответствует параболе; «минус»- эллипсу.
Лекция 8. Скорость орбитального полета и время существования ИСЗ. Типы орбит ИСЗ.
Вычислим скорость ИСЗ в некоторых точках орбиты:
1. Скорость ИСЗ в перигее:
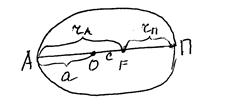
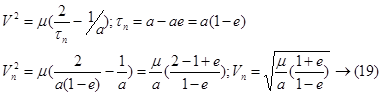
2. Скорость ИСЗ в апогее: 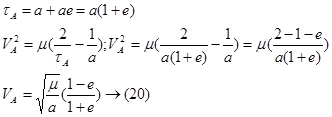
3. Найдем отношение скоростей:
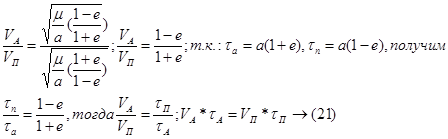
Секториальная скорость ИСЗ величина постоянная.
Первая и вторая (круговая и параболическая) космические скорости.
1. Рассмотрим круговую орбиту a=τ
Так как 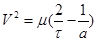 , то
, то 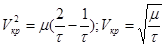
2. Для параболической орбиты: а=∞ ;
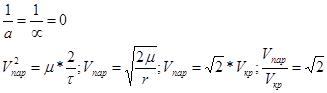
При скорости Vкр спутник движется вокруг притягивающего тела по круговой орбите. При этом сила притяжения равна центральной силе.
Параболическая скорость или скорость освобождения- это скорость выхода тела из сферы Земного притяжения. Тело, движущееся с параболической скоростью вокруг центрального тела, при отсутствии вблизи других притягивающих тел, будет неограниченно удаляться от центрального тела.
Вычислим скорость тела при его выходе из сфер притяжения Земли, если:
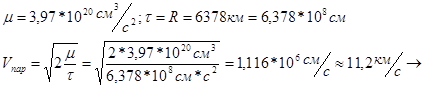 это вторая космическая скорость.
это вторая космическая скорость.
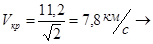 первая космическая скорость.
первая космическая скорость.
Обладая второй космической скорость, объект покинет Земную поверхность и удалиться на бесконечное расстояние, если не будет других притягивающих тел, кроме Земли.
Однако, в действительности тело, покинувшее Землю с такой скоростью, не уйдет в бесконечность, а будет двигаться по эллиптической орбите вокруг Солнца.
Период обращения и время существования ИСЗ.
Известно, что площадь эллипса 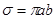 где а,б –полуоси эллипса.
где а,б –полуоси эллипса.
Если Т-период обращения по орбите, то удвоенная секториальная скорость 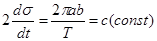 (22)
(22)
Подставим в (22) следующие значение:
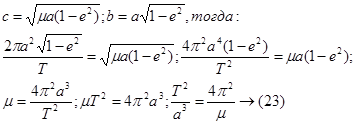
Получим аналитическое выражение 3его закона Кеплера. Обозначим: 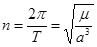 - среднее движение по эллиптической орбите.
- среднее движение по эллиптической орбите.
Из (23) найдем: 
Определим период обращения ИСЗ при следующих данных:
НА=1880км; НП=230км; μ=3,97*1020см3/с2; 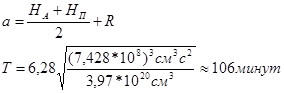
Время существования приведем в виде таблицы:
| круговая орбита | эллиптическая орбита | |||||
| высота(км) | время сущ-я(суток) | высота апогея (км) | высота перигея (км) | |||
| 0,4 | ||||||
В таблице приведено время существования для ИСЗ весом 100кг и диаметром 1м, в зависимости от начальной высоты для круговой и эллиптической орбит. Из таблицы видно, что время существования ИСЗ очень сильно зависит от высоты орбиты. При высоте полета в несколько тысяч км движение ИСЗ происходит за пределами атмосферы, и такой ИСЗ практически может оставаться постоянным.
Типы орбит ИСЗ.
В зависимости от наклона орбиты (J) ИСЗ делятся на:
1. Экваториальные (J=0)
2. Наклонные (0 < J < 90)
3. Полюсные (полярные) (J=90)
Экваториальные ИСЗ будут всегда пролетать над экватором. При Н≈36000км период обращения ИСЗ будет равен периоду обращения Земли вокруг оси. Тогда ИСЗ все время будет находиться над одним и тем же наземным пунктом. Такой спутник называется стационарным.
Экваториальный спутник можно наблюдать в полосе, примыкающей к экватору. Ширина этой полосы зависит от высоты ИСЗ.
Витки полюсного ИСЗ при каждом новом обороте будут смещаться к западу из-за вращения Земли вокруг оси. Такие ИСЗ в различное время будут наблюдаться в любом пункте Земной поверхности.
Наклонные ИСЗ проектируются на поверхность Земли только в пределах широты ∆φ=±J.
Все ИСЗ разделяются на прямые и обратные. Прямые перемещаются в направлении вращения Земли с запада на восток, обратные перемещаются с востока на запад.
При запуске прямых ИСЗ к линейной скорости ракеты добавляется линейная скорость вращения Земли. При запуске обратных ИСЗ линейная скорость движения Земли вычитывается из скорости ракеты, т.е. ракету следует разгонять на большую скорость.
Кроме перечисленной классификации спутники и их орбиты делятся на: периодические, непериодические, т.е. положение ИСЗ относительно земной поверхности каждые сутки повторяется или нет.
ИСЗ, орбиты которых лежат на границе земных дня и ночи, называются сумеречными. Их удобно наблюдать визуально, т.к. над всеми наблюдателями они будут пролетать в местные сумерки.
По высоте орбиты ИСЗ деляться на 3 группы:
1. Н до 500км (ИСЗ из серии «Космос», космические корабли и орбитальные станции)
| <== предыдущая страница | | | следующая страница ==> |
| | | Н от 500 до 2000км (метеорологические, геодезические, астрономические и др.) |
Дата добавления: 2014-03-24; просмотров: 927; Нарушение авторских прав

Мы поможем в написании ваших работ!