Метод прямоугольного треугольника

Данный метод позволяет определить натуральную величину отрезка прямой общего положения и углов наклона его к плоскостям проекций.

На рисунках 1.18 и 1.19 видно, что натуральная величина отрезка АВ прямой общего положения является гипотенузой прямоугольного треугольника АВВ_1. В этом треугольнике катет АВ₁ параллелен горизонтальной плоскости проекций и равен по длине горизонтальной проекции отрезка ab, а величина второго катета равна разности расстояний точек В и А до горизонтальной плоскости проекций ( Á ВВ₁ Á ã Z_B - Z_A ã DZ.

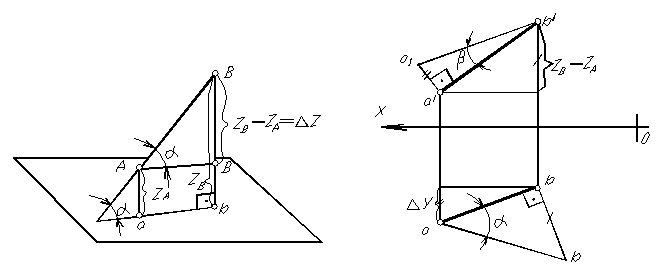
Рис. 1.18 Рис. 1.19

Нахождение натуральной величины и углов наклона отрезка прямой на комплексном чертеже показан на рисунке 1.19. В качестве одного катета принята горизонтальная (фронтальная) проекция ab, длина другого катета – разность зетовых координат точек В и А -D Z (разность игрековых координат точек В и А- D Y). Длина гипотенузы ab₁ (a₁ b^/ ) равна длине отрезка AB.

Итак, натуральную величину отрезка определяют как гипотенузу прямоугольного треугольника, одним из катетов которого является горизонтальная (фронтальная) проекция отрезка, другим – разность координат концов отрезка до горизонтальной (фронтальной) плоскости проекций.

Угол между отрезком прямой линии и плоскостью проекций определяется как угол между прямой и ее проекцией на эту плоскость. На рисунке 19 таким углом между отрезком прямой АВ и горизонтальной плоскостью проекций является угол a .

Величина угла a (рис. 1.19) определяется из того же треугольника bab₁ , что и натуральную величину отрезка АВ. Угол b - угол наклона отрезка прямой к фронтальной плоскости проекций определяется из треугольника

a^/ b^/ a₁, построенного на фронтальной проекции отрезка.

Возможно решение обратной задачи, когда задана натуральная величина отрезка и одна из ее проекций, либо одна из ее проекций и угол наклона отрезка к какой-либо плоскости проекций.

Дата добавления: 2014-04-16; просмотров: 1807; Нарушение авторских прав

Мы поможем в написании ваших работ!