Метод вращения вокруг линии уровня

(частный случай метода вращения)

Суть метода заключается в том, что осью вращения выбирается одна из линий уровня - горизонталь или фронталь. Таким образом, плоскость как бы поворачивается вокруг некоторой оси, принадлежащей этой плоскости, до положения, параллельного одной из плоскостей проекций.

Например, повернем плоский угол, образованный пересекающимися прямыми а и b (рис. 9.6).

Для решения поставленной задачи проводят в плоскости угла линию уровня (в данном случае горизонталь h) и используют ее как ось вращения, вокруг которой будут вращаться прямые аи bи вершина К. Все точки вращаются в плоскостях, перпендикулярных к горизонтали, при этом положение точек 1 и 2 остается неизменным, а точка К вращается вокруг горизонтали. Из горизонтальной проекции К₁точки К проводят линию, перпендикулярную к оси вращения h₁. Отрезок K₁O₁- горизонтальная проекция радиуса вращения точки К. Находят натуральную величину этого радиуса (например способом прямоугольного треугольника).

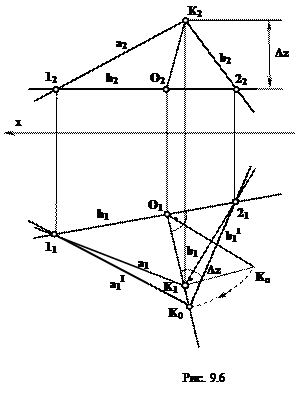На продолжении проекции прямой O₁K₁откладывают натуральную величину радиуса О_к и получают положение т.К после поворота (К₀). Соединив точки 1₁ и 2₁с точкой К₀, получают натуральную величину угла при вершине К.

Этим методом находится натуральная величина любой плоской фигуры, занимающей общее положение в пространстве.

Дата добавления: 2014-04-19; просмотров: 447; Нарушение авторских прав

Мы поможем в написании ваших работ!