МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЕ И ОПТИЧЕСКИЕ СВОЙСТВА ДИСПЕРСНЫХ СИСТЕМ. Движение частиц в дисперсных системах

В свободнодисперсных системах с газовой и жидкой дисперсионной средой (аэрозоли, коллоидные растворы, газовые эмульсии, мицеллярные растворы ПАВ) дисперсные частицы не фиксированы в каких-либо позициях. Напротив, они перемещаются; кроме того, частицы могут вращаться и совершать колебания с разной амплитудой. Подвижность дисперсных частиц – фундаментальное свойство свободнодисперсных систем.

Движение дч обусловлено различными факторами и зависит главным образом от их размера. Высокодисперсные частицы благодаря своим малым размерам активно участвуют в броуновском движении.

Броуновское движение дч рассматривают как проявление молекулярно-кинетических свойств дисперсных систем.

Другое молекулярно-кинетическое свойство – диффузия дч – процесс переноса вследствие различия их концентрации в разных областях дисперсной системы. Диффузия приводит к постепенному выравниванию концентрации частиц. В соответствии со вторым началом термодинамики диффузия сопровождается увеличением энтропии дисперсной системы.

Крупные дч (твердые частицы, капли, газовые пузыри) в броуновском движении практически не участвуют. Соответственно грубодисперсные системы не обладают молекулярно-кинетическими свойствами.

Основной причиной движения крупных дисперсных частиц служит различие плотностей дф (ρ_d) и дс (ρ_о). если плотность дф больше (ρ_d > ρ_о ), частицы постепенно оседают под действием силы тяжести. Этот процесс называют седиментацией. Более легкие дч (при условии ρ_d < ρ_о), напротив, постепенно всплывают вверх. Этот процесс называют обратной седиментацией.

Седиментация твердых частиц. Седиментация – это процесс осаждения дисперсных частиц в дисперсионной среде (дс) (обычнов жидкости) под действием силы тяжести.

Седиментация – переход частиц дисперсной фазы из объема на границы раздела фаз под действием сил разной природы (гравитационной, центростремительной, электрической).

Рис.4.6. Фролов с 121.

Способность дисперсной системы сохранять во времени равномерное распределение частиц по всему объему системы называется седиментационной или кинетической устойчивостью. Седиментационной устойчивостью обладают высокодисперсные системы (аэрозоли, лиозоли) с размером частиц 1 мкм < Q < 1 нм. Грубодисперсные системы (пыль, суспензии, эмульсии) седиментационно неустойчивы.

В результате взаимодействия противоположно направленных потоков диффузии и седиментации в системе с жидкой или газообразной дисперсионной средой устанавливается седиментационное равновесие, которое определяется различными силами, действующими на частицу: силой тяжести, архимедовой силой выталкивания, силой трения, обобщенной силой, определяемой тепловым движением частиц дисперсной фазы и молекул дисперсионной среды.

Рассмотрим оседание одной частицы дисперсной фазы.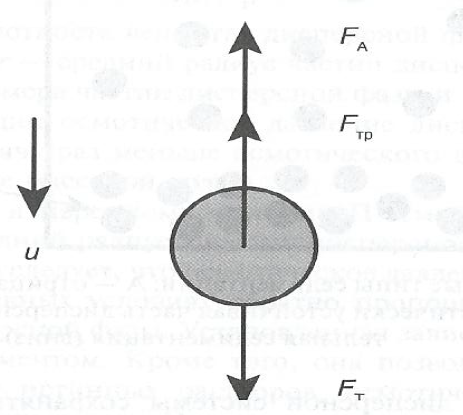

Оседание частицы в лиозоле или аэрозоле определяется суммарной силой :

F_C = F_T – F_A – F_ТP,

где F_T – сила тяжести, действующая на частицы; F_A – выталкивающая архимедова сила; F_ТP – сила трения, которая тормозит движение частицы в дисперсионной среде.

Согласно 2-му закону Ньютона, оседание частицы происходит с постоянной скоростью и, когда равнодействующая всех сил F_C равна нулю:

F_T – F_A – F_ТP = 0

Сила тяжести: F_T = mg, где т – масса чатицы дисперсной фазы, кг; g – ускорение силы тяжести, равное 9,8 м/с².

Выталкивающая архимедова сила F_A = m_жg, где m_ж – масса дисперсной фазы в объеме V частицы.

Массы m и m_ж соответственно равны m = ρV, m_ж = ρ₀V, где V – объем частицы, ρ, ρ₀ – плотности дисперсной фазы и дисперсионной среды, кг/м³. =>,

F_T = ρVg, F_A = ρ₀Vg.

Согласно закону Стокса, сила трения, действующая на сферическую частицу, пропорциональна ее радиусу r, скорости движения и коэффициенту вязкости среды η:

F_ТP = 6πrηu.

Объем сферической частицы v = 4/3πr³, =>

4/3πr³(ρ - ρ₀)g = 6πrηu

Скорость и оседания частиц равна

и = 2/9 ∙ r²/η ∙( ρ - ρ₀)g

ð Скорость оседания частиц под действием силы тяжести прямо пропорциональна квадрату радиуса частицы, разности плотностей дисперсной фазы и дисперсионной среды и обратно пропорциональна коэффициенту вязкости среды.

На основе полученной формулы по скорости оседания можно рассчитать средний размер частиц дисперсной фазы:

.

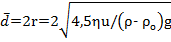Седиментационный анализ – определение свойств дисперсионной системы на основе изучения седиментации. Одним из наиболее простых и часто используемых методов седиментационного анализа является гравиметрический метод. Он основан на определении скорости накопления осадка на чашке весов, помещенной в дисперсию.

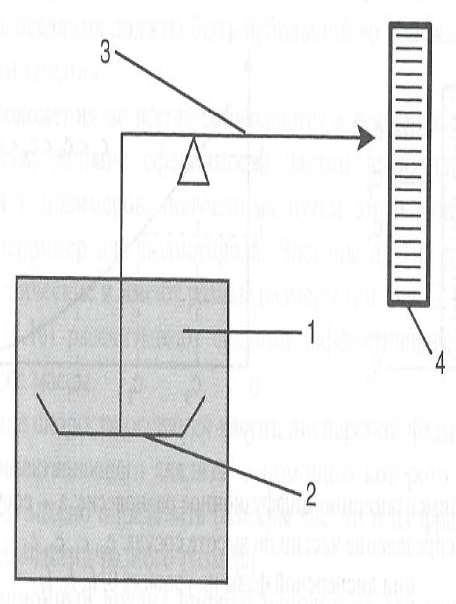
На рисунке приведена схема гравиметрического седиментометра. После тщательного перемешивания в сосуд 1 с дисперсией погружают чашку весов 2. Затем в ходе седиментации визуально или автоматически фиксируется масса m_с осадка на чашке весов в разные моменты времени.

В настоящее время для изучения седиментации широко используют торсионные весы. К коромыслу которых прикрепляется чашечка для накопления осадка. Автоматизацию измерений осуществляют путем подключения приборов с пьезодатчиками, которые преобразуют измерение массы чашечки с осадком в измерение электрического сигнала. Этот сигнал отображается при помощи самописца или на мониторе компьютера.

На основе полученных данных строят седиментационную кривую – кинетическую кривую зависимости массы m_с от времени t . 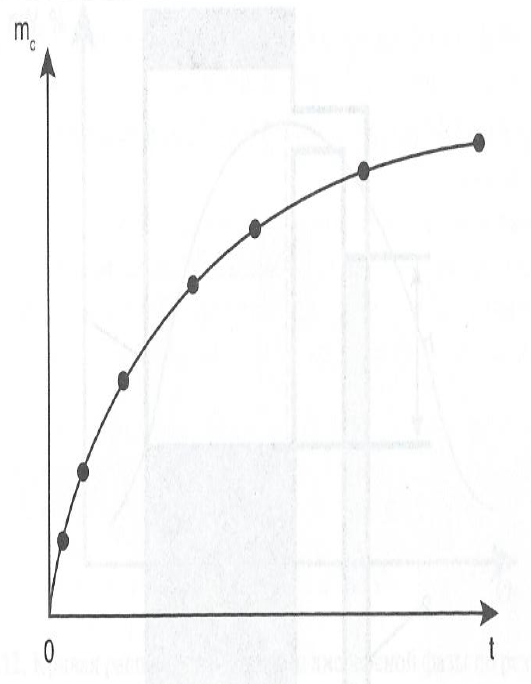Вначале масса осадка нарастает быстро, так как оседают и крупные, и мелкие частицы. Затем накопление осадка замедляется, т.к. оседают только мелкие частицы, а крупные уже осели. Плато на кривой соответствует области седиментационного равновесия.

Недостаток гравиметрического анализа – неопределенность первоначального момента осаждения, что вносит погрешность и в определение конечной массы осадка. Как правило, конечная масса осадка оказывается меньше массы, рассчитанной по концентрации и объему дисперсии в сосуде над чашечкой.

Броуновское движение и диффузия дисперсных частиц. Броуновское движение – это хаотическое движение дисперсных частиц в дисперсионной среде. Его главная особенность состоит в том, что частица перемещается хаотически. Эти скачки совершаются с большой частотой в произвольном направлении, т.е. независимо от того, каким был предшествующий скачок. Кроме того, скачки имеют разную длину. Направление движения частицы может изменяться до 10²⁰ раз в течение 1 с (рис. 2.2 Сумм).

Поскольку частица движется хаотически, то спрогнозировать точку, где окажется частица размером d за время t нельзя. Поэтому рассчитаем каким будет наиболее вероятное (среднеквадратичное) расстояние 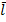от исходной точки через время t.

Перемещение дисперсной частицы при броуновском движении определяется уравнением Эйнштейна:

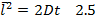
где D - коэффициент диффузии дисперсных частиц, м²/с.

Коэффициент диффузии равен массе вещества, перенесенного вследствие диффузии через единицу площади поперечного сечения стационарного диффузионного потока за единицу времени под действием единичного градиента концентрации (grad C = -1 г/см²).

Коэффициент диффузии сферической дисперсной частицы радиусом r определяется уравнением Эйнштейна:

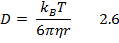
где k_B – постоянная Больцмана, равная 1,38∙10^-23 Дж/К; Т – температура, К; η – вязкость дисперсионной среды, Па∙с.

Движущая сила броуновского движения создается тепловыми колебаниями молекул жидкости, окружающей частицу. Средняя энергия этих колебаний в расчете на одну степень свободы равна 1/2 k_BТ. силу сопротивления создает вязкое трение жидкости, которое определяется уравнением Стокса (2.2).

В соответствии с уравнением (2.6) коэффициент диффузии дисперсных частиц изменяется обратно пропорционально их размеру d = 2r. Поэтому броуновское движение и диффузия присущи именно высокодисперсным и ультрадисперсным частицам.

Коэффициент диффузии резко растет с увеличением температуры. Зависимость D = f(T) определяется возрастанием энергии тепловых колебаний k_BТ. вместе с тем, вязкость жидкостей с увеличением температуры уменьшается.

Диффузия дисперсных частиц. Диффузия молекул, атомов, ионов, дисперсных частиц – один из основных процессов, происходящих в газах, жидкостях и твердых телах.

Диффузия – самопроизвольный процесс выравнивания концентрации какого-либо вещества в газе, жидкости или твердом теле.

В соответствии со 2-м началом термодинамики в-во самопроизвольно диффундирует из области с большим химическим потенциалом m₁ (концентрация больше) в область с меньшим потенциалом m₂ (концентрация меньше).

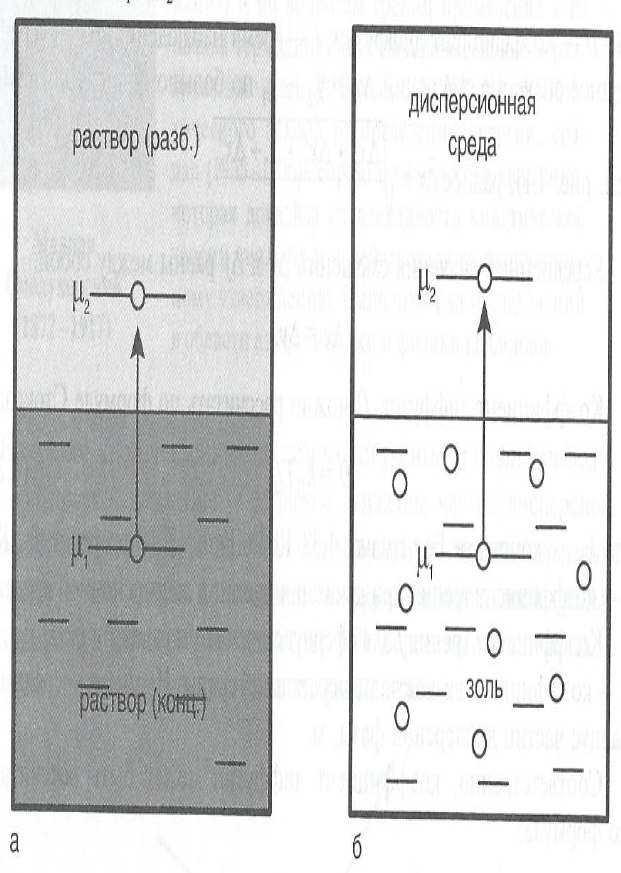Положительный заряд в электрическом поле также самопроизвольно движется от большего потенциала к меньшему: m₁ > m₂.

Диффузия дч происходит под влиянием броуновского движения и ведет к увеличению энтропии системы.

Диффузия частиц дисперсной фазы, как и молекул в растворах, описывается законом Фика, согласно которому скорость диффузии прямо пропорциональна площади поверхности, через которую проходит вещество, и градиенту его концентрации:

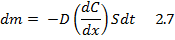
dm – масса вещества, прошедшего за время dt (с) через поверхность площадью S (м²); D – коэффициент диффузии (м²/с); с – концентрация вещества (кг/м³); dC/dx – градиент концентрации (кг/м⁴).

Знак « - » показывает, что диффузия идет в направлении уменьшения концентрации.

Физический смысл коэффициента диффузии D: коэффициент диффузии дисперсных частиц равен массе дисперсной фазы вещества, которое продиффундировало через единицу площади в единицу времени при градиенте концентрации, равным 1.

Коэффициент диффузии обратно пропорционален радиусу частицы r, поэтому диффузия происходит достаточно интенсивно только в ультрадисперсных и высокодисперсных системах.

Все экспериментальные методы измерения коэффициента диффузии D основаны на приведении в контакт чистого растворителя (дисперсионной среды) с раствором (золем). При тщательном термостатировании через определенные промежутки времени отбирают пробы в разных точках системы и анализируют их, определяя концентрацию вещества. На основании этих данных рассчитывают градиент dC/dx и коэффициент диффузии по закону Фика.

Экспериментальное определение Δх осуществляют путем простого измерения смещения границы дисперсной фазы за время t в результате броуновского движения частиц в системе золь - дисперсионная среда

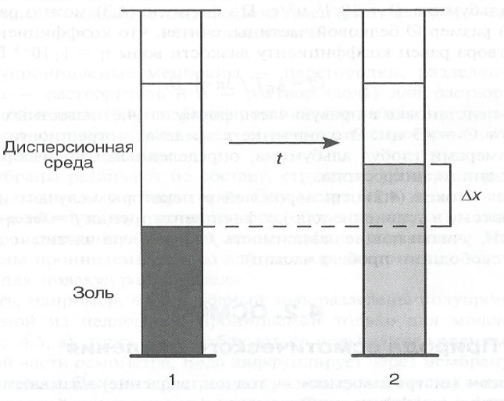
Осмос – преимущественная диффузия растворителя (дисперсионной среды) через полупроницаемую мембрану из раствора или золя с меньшей концентрацией в раствор или золь с большей концентрацией.

Необходимое условие осмоса – наличие растворителя и раствора или растворов различной концентрации, разделенных полупроницаемой мембраной.

В дальнейшем поток уравновешивается возникающим встречным градиентом давления. Этот процесс обусловлен, в термодинамической трактовке, ростом энтропии смешения системы, а в кинетической – избыточным числом ударов молекул растворителя о мембрану со стороны более разбавленного раствора.

Осмотическое давление жидких дисперсных систем, как и молекулярных растворов, подчиняется закону Вант-Гоффа:

П = cRT,

где с – молярная концентрация частиц дисперсной фазы, моль/л.

Осмотическое давление в дс очень мало, что связано, как и в случае диффузии, с относительно большим размером частиц. Осмотическое давление дисперсных систем определяется не количеством вещества, а числом частиц дисперсной фазы, поэтому для расчета необходимо заменить молярную концентрацию с на частичную концентрацию с_ν, а газовую постоянную R на константу Больцмана k_B, так как cR = n k_B.

Частичная концентрация – величина, измеряемая числом частиц N дисперсной фазы в единице объема V:

n = N/V.

При подстановке в формулу Вант-Гоффа получают выражение закона Вант-Гоффа для расчета осмотического давления дисперсных систем:

П = nk_BT.

ð Осмотическое давление дисперсных систем пропорционально частичной концентрации с_ν дисперсной фазы (числу частиц в единице объема).

Число частиц N дисперсной фазы N = m / m_ч, где m – масса дисперсной фазы в данном объеме V; m_ч – средняя масса частиц дисперсной фазы.

=> Частичную концентрацию (число частиц в единице объема) можно определить как отношение массы дисперсной фазы m, находящейся в объеме системы V, к массе коллоидной частицы m_ч : n = m / m V.

=> n = с_m / m,

где с_m – массовая концентрация вещества дисперсной фазы (кг/м³).

Подставляя это значение с_ν в закон Вант-Гоффа, получаем:

П = (с_m / m_ч )∙ k_B Т.

Принимая, что коллоидная частица имеет шаровидную форму с радиусом r, получаем:

m_ч = 4 / 3πr³ρ ,

где ρ – плотность дисперсной фазы.

Тогда закон Вант-Гоффа можно преобразовать к виду:

П = 3mk_BТ / 4πVr³ρ.

Из-за большого размера частиц дф и малых значений частичной концентрации осмотическое давление дисперсных систем приблизительно в 1000 раз меньше осмотического давле ния истинного раствора такой же массовой доли.

Течение дисперсных систем. Свободнодисперсные системы с жидкой и газовой дисперсионной средой (золи, суспензии, эмульсии, пены, аэрозоли) характеризуются большой подвижностью.

Под действием внешних воздействий: гидростатического давления, электрического напряжения – возникает течение жидкости или газа, которое увлекает находящиеся в них дисперсные частицы. Т.о. происходит перемещение всей дисперсной системы. Основная проблема заключается в учете влияния размера, формы и концентрации дч на скорость течения.

В свободнодисперсных системах основную роль играют гидродинамические эффекты, возникающие при взаимодействии частиц с жидкостью или газом. При большой концентрации частицы начинают контактировать между собой. Возникающая структура значительно уменьшает текучесть дисперсионной среды и течение может полностью прекратиться.

Рассмотрим следующую задачу: по трубке длиной l достаточно большого диаметра d = 2r (несколько см или больше) под действием перепада давления на ее концах (Δр) течет коллоидный раствор (золь) – взвесь твердых частиц в жидкости. Для упрощения будем рассматривать монодисперсную систему, т.е. все дисперсные частицы имеют одинаковый размер. Также примем, что все частицы имеют сферическую форму, а концентрация частиц ν мала, поэтому они находятся далеко друг от друга и не контактируют между собой.

При отсутствии дч, т.е. при течении однородной жидкости вязкостью η, средняя скорость ламинарного течения (v) определяется законом Пуазейля:

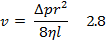
При таком же перепаде давления Δр течение дисперсной системы (коллоидного раствора) происходит с меньшей скоростью. А.Эйнштейн объяснил это тем, что присутствие дч приводит к возрастанию вязкости дисперсной системы (η^*) по сравнению с вязкостью жидкости η, т.е. η^* > η. Теория Эйнштейна определяет вязкость дс следующим уравнением:

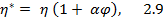
где φ – объемная доля дисперсной фазы; a – безразмерный коэффициент, который зависит от формы дч.

Для сферических частиц a = 2,5; для анизодиаметрических частиц (эллипсоидов, стержней и т.д.) a имеет более высокое значение. Чем больше вытянутость частицы, тем больше коэффициент a.

В соответствии с (2.9) вязкость коллоидной системы зависит от общего количества дч (от объемной доли дисперсной фазы), но не зависит от размера частиц.

Уравнение Эйнштейна можно преобразовать к форме:

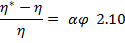
Дробь слева характеризует относительное увеличение вязкости дс при введении в нее дф; оно растет линейно при увеличении объемной доли дф.

Уравнение (2.10) позволяет по экспериментальной зависимости η^* = f(φ)определить коэффициент a, зависящий от формы частиц. Эти данные в свою очередь используют для оценки размера дч и макромолекул.

Дата добавления: 2014-04-28; просмотров: 1026; Нарушение авторских прав

Мы поможем в написании ваших работ!