Индексы видового богатства

Для оценки видового богатства сообществ часто используются различные индексы. Среди них наиболее простыми являются:

1) Индекс видовой плотности, отражающий число видов на единицу площади; у ботаников, например, число видов растений на 1 кв.м;

2) Индекс нумерического видового богатства – число видов на определенное количество особей; у гидрологов, например, 20 видов на 1000 особей. Более сложные индексы отражают соотношение между числом видов и числом особей,вт.ч.

3) Индекс видового богатства Минхиника

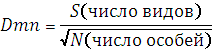
4) Индекс видового богатства Маргалефа

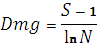
У этих двух индексов большая величина соответствует большему разнообразию. Еще более сложными являются индексы, учитывающие видовое богатство и выравненность (т.е численность отдельных видов). Среди них наиболее популярными являются:

5) Индекс Шеннона

гдеp1 – доля каждого вида

6) Индекс Бриллуэна

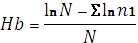
Как видите, его определение требует более сложных расчетов, в связи с чем употребляется реже, хотя дает величины сходные с индексом Шеннона.

Существует также ряд индексов,отражающих степень доминирования в сообществах, в т.ч.

7) Индекс Симпсона, который рассчитывается по формуле

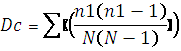
Где n1- число особей одного вида

N- числоособейвсехвидов

8) Индекс Бергера-Паркера, хорошо отражающий относительное значение любого вида в сообществе, который рассчитывается по формуле

=

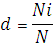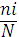
На величину его не влияет количество видов, поскольку расчет ведется лишь по величине выборки.

9) Индекс (мера разнообразия) Макинтоша, который рассчитывается по формуле

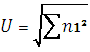. Однако сам по себе он не является индексом доминирования, но используя его значение можно рассчитать меру доминирования D1, которая независима от выборки.

и выравненность

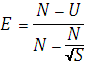
10) В тоже время считается, что наиболее точно доминирование отражает индекс полидоминантности

.

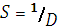5. Анализ β - разнообразия сообществ.

Этот показатель(предложенный Уиттекером в 1960 г.) характеризует сходство или различие разных местообитаний по видовому составу и численности слагающих их видов, а в некоторой степени дает представление и по общему разнообразию условий территории. Его применяют также при сравнении сезонной динамики состава сообществ, изменении степени пищевой специализации видов, оценке загрязнения водоемов и наземных сообществ и т.п.

При оценке данных о присутствии или отсутствии видов в сообществах обычно используют разные меры или критерии измерения β-разнообразия, но большинству критериев соответствует мера Уиттекера. Данные о сходстве/ различии обычно устанавливаются в абсолютных или относительных значениях.

При сравнении сообществ учитывают следующие показатели:

-a-число видов, общих для двоих сообществ;

-b- число видов, имеющихся только в одном сообществе;

-c- число видов, имеющихся только в другом сообществе.

На их основе рассчитываются значения a+b, a+c, a+b+c, а также отрицательные совпадения (несовпадения).

Для биоценотических, фаунистических и биогеографических исследований предложено более 10 индексов, но чаще всего используются индексы:

1. Жаккара 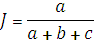,т.е. рассчитывается отношение количества общих видов, к объединенному количеству;

2. Чекановского-Серенсена, т.е. отношение видов к среднеарифметическому числу видов в двух сообществах.

Из числа индексов, учитывающих негативные совпадения (т.е несовпадения) наиболее простыми являются индексы:

3. Кульчинского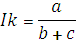

4. Сокала-Майченера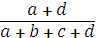

При расчете индексов общности для количественных данных наиболее приемлемо использование коэффициента Серенсена

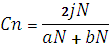, где делимое- сумма наименьших обилий;делитель- общее число особей на участках а и б.

При расчете тех или иных показателей обычно проводится их группирование и классификация. Эти процедуры выполняются преобразованием полученных расчетных данных (матрицы) в различные графики или диаграммы.

6. Графический анализ β- разнообразия.

Сетевой анализ матриц оценок сходства между объектами заключается в построении различных графиков или фигур, на которых степень сходства между объектами отражается взаимным расположением точек или разными особенностями линий, соединяющих эти точки.

Наиболее простыми являются неориентированные графы, в которых точки соединяются линиями, не имеющими определенного направления (в ориентированных точки соединяются стрелками). Одним из типов неориентированного графа является дендрит- ломанная линия, которая может ветвится. Его построение заключается в последовательном соединении линий двух наиболее сходных выборок по данным матрицы сходства выборочных совокупностей, вычисленных на основе индекса сходства Жаккара (таблица, рисунок). Следует отметить, что на таком графе отображаются только максимальные значения соответствия, а следовательно, часть информации теряется.

Более полно,т.е вся матрица сходств отображается графом «плеяд», предположенным нашим известным зоологом Терентьевым П.В. В его разных вариантах взаимосвязи могут отражаться различными линиями или одинаковыми линиями, но на разных уровнях сходства.

При одновременном сравнении сходства нескольких сообществ хорошее представление о β – разнообразии даст кластерный анализ, в котором несколько объектов разделяются на однородные группы (кластеры). Графически это отображается в виде дендрограммы.

В наиболее простых случаях группировка начинается с нахождения в матрице индексов сходства пары наиболее похожих объектов (0,9), к которым постепенно присоединяются другие. Это присоединение можно произвести тремя разными способами: одиночным, средним и полным присоединением.

Одиночное присоединение ( метод ближнего соседа) проводится по максимальному значению сходства между объектами каждой группы (к ДГ присоединяется В, затем объединяются Аи Б, Е присоединяется к ДГВ и, наконец, оба кластера объединяются на уровне 0.6. При среднем присоединении последующие объекты присоединяются по среднеарифметическому значению сходства с объектами группы.При полном присоединении (метод дальнего соседа) присоединение осуществляется по минимальному сходству объекта с другими объектами этого кластера.

Более сложные и разнообразные методы кластерного анализа реализуются с помощью вычислительной техники для которой разработан ряд статистических пакетов программ, в том числе таких, как Statistica, Statgaphics и другие.

Дата добавления: 2014-04-28; просмотров: 2687; Нарушение авторских прав

Мы поможем в написании ваших работ!