Динамика идеальной жидкости

4.1. Дифференциальное уравнение движения идеальной жидкости (при устано­вившемся движении) и его интегрирование

Для вывода уравнения движения жидкости обратимся к записанному ранее уравне­нию равновесия жидкости (в проекциях на координатные оси), иначе говоря: 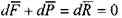. Поскольку в идеальной жидкости никаких сосредоточенных сил действовать не может, то последнее уравнение чисто условное. Когда равнодейст­вующая отлична от 0, 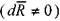то жидкость начнёт двигаться с некоторой скоро­стью, т.е. в соответствии со вторым законом Ньютона, частицы жидкости, состав­ляющие жидкое тело получат ускорение.

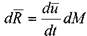
Тогда уравнение движения жидкости в проекциях на координатные оси можно запи­сать в следующем виде:

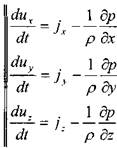
Согласно основному положению о поле скоростей (метод Эйлера) для проекций ско­ростей движения жидкости можно записать следующее:

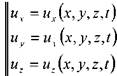
или (для установившегося движения жидкости):

Найдём первые производные от скоростей по времени, т.е. определим ускорения вдоль осей координат:

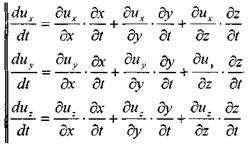
отметим, что: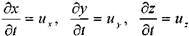

' * /

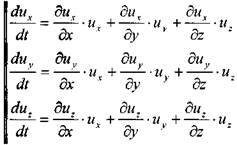
Теперь подставив выражения для ускорений в исходную систему дифференциальных уравнений движения жидкости, получим систему уравнений Эйлера в окончательном ви-де²:

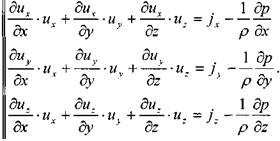
Теперь вновь обратимся к системе дифференциальных уравнений движения жидко­сти, умножив обе части 1-го уравнения на dx, 2-го уравнения на dy, 3-го уравнения на dz, получим:

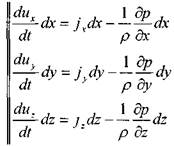
и просуммировав эти уравнения по частям, получим:

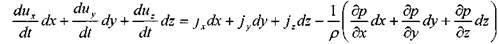
² При неустановившемся движении жидкости уравнения Эйлера дополняются первыми слагаемыми.

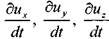
Преобразуем левую часть полученного уравнения, полагая, что

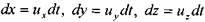в результате запишем

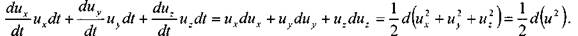
Слагаемые в правой части уравнения являются полными дифференциалами функ­ций.

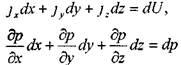
Теперь уравнение примет вид

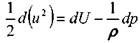
Если из массовых сил на жидкость действует только сила тяжести, то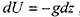, и

> ,*

тогда получим:

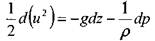
После интегрирования получим:

?

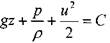разделив почленно все члены уравнения на g, получим так называемое уравнение Бернулли

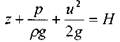
Здесь величина Н называется гидродинамическим напором Величина гидродинами­ческого напора постоянна для всех живых сечений элементарной струйки идеальной жид­кости.

Дата добавления: 2014-02-26; просмотров: 501; Нарушение авторских прав

Мы поможем в написании ваших работ!