
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Понятие равновесия по Нэшу. Нахождение ситуации равновесия в биматричных играх
Социальный процесс представляет собой бесконечный динамичный поток событий. Встает вопрос о соотношении эмпирического и теоретического знания в социально-гуманитарных исследованиях.
Особенности эмпирических фактов в социогуманитарном знании:
1) Данные факты социальны по своей природе. С одной стороны, они являются инвариантными и неизменными по своей сущностной завершенности. С другой, установление и интерпретация данных фактов затруднены, так как в отличие от фактов естественных наук, они в большинстве случаев непосредственно не наблюдаемы и не воспроизводимы в эксперименте.
2) Социальные факты по своей природе динамичны, находятся в постоянном развитии, по мере, с одной стороны, общественной эволюции, с другой, совершенствования теорий и методов получения и обработки данных. Социальные факты изменяются, появляются и исчезают в зависимости от принятой точки зрения, масштабов исследования, исследовательского интереса, концептуальной системы.
Важной проблемой для исследователя является отбор социальных фактов. Его задачей выступает приведение в порядок социальных явлений, а для этого необходима теория, на основании которой осуществляется избирательный подход к социальным фактам. Отбор социальных фактов тесно связан с ценностными установками исследователя и его научной концепцией. Освещение социальных явлений в различных исследованиях может значительно отличаться. Противоборствующие научные концепции диктуют неодинаковый отбор фактов в работах ученых различных направлений, способствуют созданию отличающихся моделей социальной действительности. Оперируя социальными фактами, исследователь обладает относительной свободой, от него зависит отбор фактов и построение их в известную систему, а также итоговая оценка событий. Вместе с тем исследователь не имеет права абсолютно произвольно обходиться с фактами.
Для отражения социальных явлений требуется введение пространственно-временных и смысловых границ, которые всегда относительны (что считать началом гражданской войны в России, например).
Особенности социально-гуманитарных теорий:
Теории в социально-гуманитарных науках не носят дедуктивного характера, т.е. не представляют собой такой хорошо организованной связи между положениями, чтобы можно было из одного вывести любое другое. В социально-гуманитарных теориях отсутствует строгость такого порядка, как, например, в теориях математики или логики. В таких условиях особенно важное место в исследовании начинает занимать гипотеза. Отсюда важнейшее звено социально-гуманитарного исследования – формулирование гипотез. Одна из причин слабости многих исследований – отсутствие в них гипотез или неграмотное их построение. Гипотезы особенно важны в социально-гуманитарном знании, где затруднено применение экспериментальных методов исследования.
С другой стороны, как бы ни сложно было построение теорий в социально-гуманитарных науках, более или менее полное знание и здесь не может развиваться при отсутствии теоретических обобщений. Характерная особенность – наличие ряда конкурирующих гипотез и теорий, которые различным образом объясняют те или иные социальные явления (в отличие от естественных наук).
В социально-гуманитарных исследованиях затруднена проверка гипотез. Гипотезы в большинстве случаев сами по себе не доказательны, они являются не результатом всестороннего исследования, а вытекают из общих соображений, отдельных наблюдений, интуитивных соображений. Обоснование научных гипотез осуществляется наличным материалом. Обосновать гипотезу – не означает перечислить все социальные факты. Нужно дойти до их сути. А этого невозможно достигнуть без предварительных рассуждений и общих представлений. Поэтому опыт здесь в большей степени теоретически нагружен, чем в естественных науках.
Специфика постижения истины в социально-гуманитарных исследованияхРазличие подходов к пониманию истины в рамках методологии науки в целом содействовало формированию разных позиций в понимании истины в социально-гуманитарных науках. Сторонники классической концепции истины и ее неклассических модификаций отстаивают положение о том, что всякое социогуманитарное знание может считаться истинным тогда, когда оно соответствует принципу объективности (позитивизм, марксизм, структурализм). С точки зрения данной позиции объективность социально-гуманитарного знания обеспечивается следующими факторами:- всесторонний охват изучаемого явления с целью выявления его сущности и многообразия связей с социальным окружением;- опора на достигнутый уровень научного знания с учетом выдвинутых по данной проблеме точек зрения;- применение всей совокупности различных методов для получения из источников максимально обширной информации;- беспристрастная позиция и профессионализм исследователя. Вместе с тем представители других подходов, противостоящих классической концепции указывают на трудности, стоящие на пути объективного изучения общества:- совпадение субъекта и объекта социального познания; - чрезвычайная динамичность и нелинейность процессов социальной действительности; - принципиальная невозможность исследователя полностью отстраниться от субъективных предпочтений при анализе общественных явлений. На основании этого в ряде направлений утверждается невозможность достижения объективной истины в социальном познании. Поскольку в той или иной степени научное исследование социальных явлений включает в себя определенное отношение ученого к предмету исследования, в основе определения истины должен находиться ценностный подход.В методологии социально-гуманитарного познания ценностный подход был введен представителями баденской школы неокантианства (В. Виндельбанд, Г. Риккерт) и М. Вебером, позднее развит в постструктурализме и герменевтике. Они исходили из того, что постижение социальных действий возможно лишь в соотнесении с ценностями, задающими нормы поведения и цели деятельности человека. Неокантианцы утверждали, что существуют определенные общепризнанные достижения культуры, которые составляют безусловные ценности для человеческого бытия (как например, религия, государство, право, мораль, наука, искусство). Сущность ценностного подхода состоит в отнесении изучаемых объектов к тем или иным ценностям, благодаря чему проводится отбор объектов и их характеристика. При этом указывается на недопустимость отождествления отнесения к ценностям и субъективной оценки. Связь с практикой определяет исторический характер ценностей. Они неодинаковы у различных культурных групп, государственных образований, классов, партий, возникают и преобразовываются либо исчезают вместе с ними. Наличие ценностей обуславливает то, что анализ социальных явлений производится через их соотнесение с ценностями. Последнее представляет волевое отношение субъекта к рассматриваемому объекту, средство осознания его значимости для человека. По содержанию оно характеризуется актом логического выбора, предпочтения субъектом определенных объектов, их свойств, отношений. Оно предполагает сравнение с некоторой абстрактно сконструированной нормой. Например, возьмем изучение такого явления как «толерантность» в некотором обществе. «Толерантность» не существует сама по себе объективно, вне нашего сознания и воли, как допустим, электричество или радиоактивность. Она является ценностью, сформированной в сознании людей. Поэтому выявление феномена толерантности в обществе по сути есть соотнесение некоторых фактов с ценностью толерантности, существующей в культуре того или иного общества, на основе сравнения с нормой, раскрывающей эту ценность.В то же время в реальных социально-гуманитарных исследованиях можно заметить то, как влияние ценностей трансформируется в субъективную оценку социальных явлений. Оценочные суждения зачастую базируются на исторически и культурно ограниченных ценностных ориентациях (политических, религиозных, классовых, национальных). Воздействие последних на исследовательскую практику с трудом поддается контролю. Оно может быть и бессознательным выражением жизненной позиции ученого, и его принципиальным мнением. Нередко можно наблюдать прямое воздействие на социально-гуманитарные науки со стороны политических, идеологических, экономических, религиозных институтов путем социального заказа.Понятие равновесия по Нэшу. Нахождение ситуации равновесия в биматричных играх.
Определение 1. Ситуация бескоалиционной игры x0= (x10, …, xn0) называется ситуацией равновесия по Нэшу, если
Hi (x10, …xi-10, xi, xi+10, …, xn0 ) < Hi (x10, …xi-10, xi0 , xi+10, …, xn0 ) "i
Пояснение к определению 1: ситуация равновесия по Нэшу является устойчивой ситуацией, т.к. ни одному игроку не выгодно в этой ситуации изменять свой выбор – при смене своей стратегии (если i-тый игрок использует произвольную стратегию xiвместо входящей в ситуацию равновесия xi0) его выигрыш уменьшается. Таким образом, ни одному игроку не выгодно в одиночку менять свою стратегию, а соглашения между игроками в бескоалиционной игре запрещены.
Определение 2. Стратегия игрока, входящая хотя бы в одну ситуацию равновесия по Нэшу, называется равновесной стратегией.
Неравенства из определения 1 можно записать для ситуации равновесия в чистых стратегиях для биматричной игры с матрицами выигрыша А и В.
Определение 3. Ситуация биматричной игры x0= (i0, j0)называется ситуацией равновесия по Нэшу, если
ai j0 < ai0 j0 "i b i0 j < bi0 j0 "j
Рассмотрим алгоритм нахождения ситуации равновесия в чистых стратегиях на примере биматричной игры «Семейный спор» (из примера 1):
1)находим наибольшие выигрыши для первого игрока – это максимальные элементы по столбцам матрицы А;
2) 
 находим наибольшие выигрыши для второго игрока – это максимальные элементы по строкам матрицы В;
находим наибольшие выигрыши для второго игрока – это максимальные элементы по строкам матрицы В;
3)  элементы обобщённой матрицы, для которых оба выигрыша являются наилучшими для первого и второго игроков, являются ситуацией равновесия в чистых стратегиях.
элементы обобщённой матрицы, для которых оба выигрыша являются наилучшими для первого и второго игроков, являются ситуацией равновесия в чистых стратегиях.
Ситуациями равновесия являются ситуации (Ф, Ф) и (Т, Т) с выигрышем (4,1) и (1,4).
Проверим, что эти ситуации действительно являются ситуациями равновесия, и игрок, отклоняющийся от этой ситуации, уменьшает свой выигрыш.
Если изменяет свою стратегию первый игрок, то из ситуации ( Ф, Ф ) он переходит в ситуацию ( Т, Ф), а его выигрыш становится равен 0 вместо 4; из ситуации ( Т, Т ) переходит в ситуацию ( Ф, Т) и его выигрыш становится равен 0 вместо 1.
Аналогично, если изменяет свою стратегию второй игрок, то из ситуации ( Ф, Ф ) он переходит в ситуацию ( Ф, Т ), а его выигрыш становится равен 0 вместо 1; из ситуации ( Т, Т ) переходит в ситуацию ( Т, Ф) и его выигрыш становится равен 0 вместо 4.
Замечание: ситуации равновесия можно находить сразу по обобщённой матрице, при этом по первым компонентам находим максимум по столбцам, по вторым компонентам – максимум по строкам. Пара, в которой выделены и первая, и вторая компонента, будет являться ситуацией равновесия.
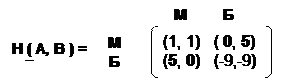 Для биматричной игры «Производство конкурирующей продукции» (из примера 2)с обобщённой матрицей выигрышей
Для биматричной игры «Производство конкурирующей продукции» (из примера 2)с обобщённой матрицей выигрышей
по первым элементам каждой пары находим максимум по столбцам (в первом столбце 5, во втором 0), по вторым элементам находим максимум по строкам (в первой строке 5, во второй 0). Эти элементы образуют две пары, следовательно, ситуациями равновесия являются ситуации (Б,М) и (М,Б) с выигрышем ( 5, 0) и ( 0 ,5).
 Для биматричной игры «Дуополия» (из примера 5)с обобщённой матрицей выигрышей
Для биматричной игры «Дуополия» (из примера 5)с обобщённой матрицей выигрышей
максимальные элементы по столбцам для первого игрока (в первом столбце 0, во втором 8) и максимальные элементы по строкам для второго игрока (в первой строке 0, во второй 8) входят одновременно только в одну пару ( 0, 0). Следовательно, ситуацией равновесия является ситуация ( Н, Н ) с выигрышем ( 0, 0).
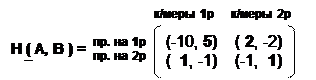 Для биматричной игры «Проникновение на рынок» (из примера 4) с обобщённой матрицей выигрышей
Для биматричной игры «Проникновение на рынок» (из примера 4) с обобщённой матрицей выигрышей
максимальные элементы по столбцам для первого игрока (в первом столбце 1, во втором 2) и максимальные элементы по строкам для второго игрока (в первой строке 5, во второй 1) не образуют пары, следовательно, ситуаций равновесия в чистых стратегиях в этой игре нет.
Действительно, если стратегия фирмы А была разгадана фирмой В, то в этой ситуации отклонение выгодно для фирмы А, в противном случае отклонение выгодно для фирмы В.
Аналогично матричным играм, в биматричных играх также можно перейти от однократной игры к её повторению несколько раз и, соответственно, рассматривать смешанные стратегии и средний выигрыш в расширенной биматричной игре.
Нахождение ситуации равновесия в смешанных стратегиях.
Определение 1. Пусть первый игрок использует смешанную стратегию X = (p1, …, pm), а второй игрок – смешанную стратегию Y = (q1, …, qn), тогда средний выигрыш первого игрока в расширенной биматричной игре:
vA = H1(X, Y) = X × A × YT,
средний выигрыш второго игрока в расширенной биматричной игре:
vB = H2(X, Y) = X × B × YT
Определение 2. Ситуация биматричной игры (X0, Y0) называется ситуацией равновесия по Нэшу в смешанных стратегиях, если
H1(X, Y0) < H1(X0, Y0) и H2(X0 , Y) < H2(X0, Y0) " X,Y
Теорема Нэша. Любая биматричная игра имеет по крайней мере одну ситуацию равновесия по Нэшу в смешанных стратегиях.
В отличие от матричных игр, биматричная игра может иметь ситуацию равновесия, как в чистых, так и в смешанных стратегиях.
В биматричной игре «Семейный спор» существует две ситуации равновесия по Нэшу в чистых стратегиях (Ф, Ф) и (Т, Т) с выигрышем (4, 1) и (1, 4). Найдём ситуацию равновесия и средний выигрыш в смешанных стратегиях для этой игры.
Пусть смешанная равновесная стратегия имеет вид X = ( p1, p2 ) = ( p, 1-p )
Найдём значение p из следующего свойства:
Утверждение. Ситуация в смешанных стратегиях является ситуацией равновесия Û ситуация устойчива относительно всех отклонений в чистых стратегиях от этой ситуации.
Смысл утверждения: если первый игрок использует смешанную равновесную стратегию X, то выигрыш второго игрока должен быть одинаковым при любой его стратегии, т.е. выбор стратегии вторым игроком не даёт ему никаких преимуществ. Тогда достаточно обеспечить равенство выигрыша второго игрока при использовании чистых стратегий Y1 = ( 1, 0) и Y2 = ( 0, 1).
Получаем матричное уравнение следующего вида:
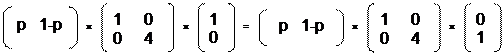 |
X × B × Y1 = X × B × Y2
Подставляем значения X, В, Y1 и Y2, получаем:
Перемножаем, получаем уравнение:
p = 4 – 4p
p = 4/5
Следовательно, смешанная равновесная стратегия первого игрока –- X = (4/5, 1/5).
Аналогичным образом находим равновесную смешанную стратегию для второго игрока. Применение равновесной смешанной стратегии Y = ( q1, q2 ) = (q, 1-q ) должно обеспечивать равный выигрыш первого игрока при использовании чистых стратегий X1 = ( 1, 0) и X2 = ( 0, 1), т.е.
X1 × А × Y = X2 × А × Y
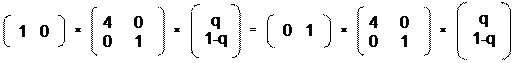 |
Подставляем значения X1, X2, A и Y, получаем:
Перемножаем, получаем уравнение:
4q = 1 – q
q = 1/5
Следовательно, смешанная равновесная стратегия второго игрока - Y = ( 1/5, 4/5).
Определим выигрыш первого и второго игроков при использовании этих равновесных смешанных стратегий:
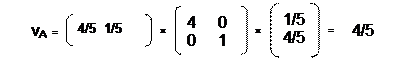 | |
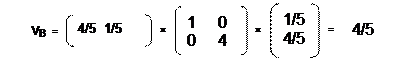 |
Получили ситуацию равновесия в смешанных стратегиях для игры «Семейный спор»: смешанные равновесные стратегии X = (4/5, 1/5) и Y = ( 1/5, 4/5) с выигрышем ( vA , vB ) = ( 4/5, 4/5 ).
Замечание 1: при использовании равновесных смешанных стратегий игроки получили средний выигрыш меньше ( 4/5 < 1 ), чем в ситуациях равновесия в чистых стратегиях (4, 1) и (1, 4), т.к. при случайном выборе стратегий могут встречаться ситуации ( Ф, Т ) и ( Т, Ф ), которые приносят обоим игрокам нулевой выигрыш, за счёт чего средний выигрыш уменьшается.
В биматричной игре «Проникновение на рынок» (из примера 4) не существует ситуации равновесия в чистых стратегиях. Проверьте (аналогично примеру с биматричной игрой «Семейный спор»), что равновесные смешанные стратегии имеют вид X = (2/9, 7/9) и Y = (3/14, 11/14), при этом средний выигрыш игроков ( vA , vB ) = = ( -4/ 7, 3/9 ).
Это означает, что фирма А должна использовать чистые стратегии 1 и 2 с частотами 2/9 и 7/9 , при этом она получит средний выигрыш vA= - 4/7, а фирма В — чистые стратегии 1 и 2 с частотами 3/14 и 11/14, средний выигрыш равен, соответственно, vB = 3/9. При отклонении одной из фирм от указанных смешанных стратегий отклонившаяся фирма уменьшает свой ожидаемый выигрыш.
Замечание 2: использование смешанных стратегий в биматричных играх может как уменьшать ожидаемый выигрыш игроков (например, в игре «Семейный спор»), так и увеличивать его.
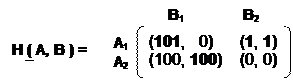 |
Рассмотрим биматричную игру с обобщённой матрицей выигрышей:
В этой игре существует ситуация равновесия в чистых стратегиях ( А1, В2 ) с выигрышем игроков ( 1, 1). Однако, если при повторении игры первый игрок будет с небольшой частотой использовать стратегию А2, то второму игроку будет выгодно от стратегии В2 перейти к стратегии В1, что приведёт к увеличению выигрыша обоих игроков.
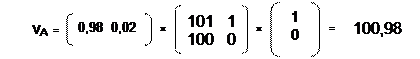 |
Например, если первый игрок будет использовать смешанную стратегию X = (0,98 ; 0,02), а второй игрок – чистую стратегию Y = (1, 0), то их средний выигрыш будет равен:
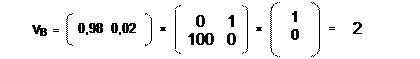 |
Таким образом, использование случайности при выборе стратегии привело к увеличению выигрыша первого игрока более чем в 100 раз и выигрыша второго игрока в 2 раза.
Уменьшение или увеличение выигрыша в биматричных играх при использовании случайного выбора стратегий зависит от условий игры – если игрокам выгоднее договариваться друг с другом (игра «Семейный спор»), то случайность только мешает, если же игроки находятся практически в антагонистических отношениях, то случайность помогает добиться большего выигрыша
| <== предыдущая страница | | | следующая страница ==> |
| Специфика концептуализации социально-гуманитарного знания. Особенности гипотез и теорий в социально-гуманитарном знании | | | Изомерия органических соединений |
Дата добавления: 2014-07-11; просмотров: 1750; Нарушение авторских прав

Мы поможем в написании ваших работ!