
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Изомерия органических соединений
Определение 1. Ситуация бескоалиционной игры x0= (x10, …, xn0) называется ситуацией равновесия по Нэшу, если
Hi (x10, …xi-10, xi, xi+10, …, xn0 ) < Hi (x10, …xi-10, xi0 , xi+10, …, xn0 ) "i
Пояснение к определению 1: ситуация равновесия по Нэшу является устойчивой ситуацией, т.к. ни одному игроку не выгодно в этой ситуации изменять свой выбор – при смене своей стратегии (если i-тый игрок использует произвольную стратегию xiвместо входящей в ситуацию равновесия xi0) его выигрыш уменьшается. Таким образом, ни одному игроку не выгодно в одиночку менять свою стратегию, а соглашения между игроками в бескоалиционной игре запрещены.
Определение 2. Стратегия игрока, входящая хотя бы в одну ситуацию равновесия по Нэшу, называется равновесной стратегией.
Неравенства из определения 1 можно записать для ситуации равновесия в чистых стратегиях для биматричной игры с матрицами выигрыша А и В.
Определение 3. Ситуация биматричной игры x0= (i0, j0)называется ситуацией равновесия по Нэшу, если
ai j0 < ai0 j0 "i b i0 j < bi0 j0 "j
Рассмотрим алгоритм нахождения ситуации равновесия в чистых стратегиях на примере биматричной игры «Семейный спор» (из примера 1):
1)находим наибольшие выигрыши для первого игрока – это максимальные элементы по столбцам матрицы А;
2) 
 находим наибольшие выигрыши для второго игрока – это максимальные элементы по строкам матрицы В;
находим наибольшие выигрыши для второго игрока – это максимальные элементы по строкам матрицы В;
3)  элементы обобщённой матрицы, для которых оба выигрыша являются наилучшими для первого и второго игроков, являются ситуацией равновесия в чистых стратегиях.
элементы обобщённой матрицы, для которых оба выигрыша являются наилучшими для первого и второго игроков, являются ситуацией равновесия в чистых стратегиях.
Ситуациями равновесия являются ситуации (Ф, Ф) и (Т, Т) с выигрышем (4,1) и (1,4).
Проверим, что эти ситуации действительно являются ситуациями равновесия, и игрок, отклоняющийся от этой ситуации, уменьшает свой выигрыш.
Если изменяет свою стратегию первый игрок, то из ситуации ( Ф, Ф ) он переходит в ситуацию ( Т, Ф), а его выигрыш становится равен 0 вместо 4; из ситуации ( Т, Т ) переходит в ситуацию ( Ф, Т) и его выигрыш становится равен 0 вместо 1.
Аналогично, если изменяет свою стратегию второй игрок, то из ситуации ( Ф, Ф ) он переходит в ситуацию ( Ф, Т ), а его выигрыш становится равен 0 вместо 1; из ситуации ( Т, Т ) переходит в ситуацию ( Т, Ф) и его выигрыш становится равен 0 вместо 4.
Замечание: ситуации равновесия можно находить сразу по обобщённой матрице, при этом по первым компонентам находим максимум по столбцам, по вторым компонентам – максимум по строкам. Пара, в которой выделены и первая, и вторая компонента, будет являться ситуацией равновесия.
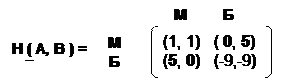 Для биматричной игры «Производство конкурирующей продукции» (из примера 2)с обобщённой матрицей выигрышей
Для биматричной игры «Производство конкурирующей продукции» (из примера 2)с обобщённой матрицей выигрышей
по первым элементам каждой пары находим максимум по столбцам (в первом столбце 5, во втором 0), по вторым элементам находим максимум по строкам (в первой строке 5, во второй 0). Эти элементы образуют две пары, следовательно, ситуациями равновесия являются ситуации (Б,М) и (М,Б) с выигрышем ( 5, 0) и ( 0 ,5).
 Для биматричной игры «Дуополия» (из примера 5)с обобщённой матрицей выигрышей
Для биматричной игры «Дуополия» (из примера 5)с обобщённой матрицей выигрышей
максимальные элементы по столбцам для первого игрока (в первом столбце 0, во втором 8) и максимальные элементы по строкам для второго игрока (в первой строке 0, во второй 8) входят одновременно только в одну пару ( 0, 0). Следовательно, ситуацией равновесия является ситуация ( Н, Н ) с выигрышем ( 0, 0).
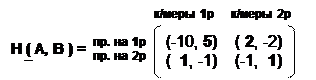 Для биматричной игры «Проникновение на рынок» (из примера 4) с обобщённой матрицей выигрышей
Для биматричной игры «Проникновение на рынок» (из примера 4) с обобщённой матрицей выигрышей
максимальные элементы по столбцам для первого игрока (в первом столбце 1, во втором 2) и максимальные элементы по строкам для второго игрока (в первой строке 5, во второй 1) не образуют пары, следовательно, ситуаций равновесия в чистых стратегиях в этой игре нет.
Действительно, если стратегия фирмы А была разгадана фирмой В, то в этой ситуации отклонение выгодно для фирмы А, в противном случае отклонение выгодно для фирмы В.
Аналогично матричным играм, в биматричных играх также можно перейти от однократной игры к её повторению несколько раз и, соответственно, рассматривать смешанные стратегии и средний выигрыш в расширенной биматричной игре.
Нахождение ситуации равновесия в смешанных стратегиях.
Определение 1. Пусть первый игрок использует смешанную стратегию X = (p1, …, pm), а второй игрок – смешанную стратегию Y = (q1, …, qn), тогда средний выигрыш первого игрока в расширенной биматричной игре:
vA = H1(X, Y) = X × A × YT,
средний выигрыш второго игрока в расширенной биматричной игре:
vB = H2(X, Y) = X × B × YT
Определение 2. Ситуация биматричной игры (X0, Y0) называется ситуацией равновесия по Нэшу в смешанных стратегиях, если
H1(X, Y0) < H1(X0, Y0) и H2(X0 , Y) < H2(X0, Y0) " X,Y
Теорема Нэша. Любая биматричная игра имеет по крайней мере одну ситуацию равновесия по Нэшу в смешанных стратегиях.
В отличие от матричных игр, биматричная игра может иметь ситуацию равновесия, как в чистых, так и в смешанных стратегиях.
В биматричной игре «Семейный спор» существует две ситуации равновесия по Нэшу в чистых стратегиях (Ф, Ф) и (Т, Т) с выигрышем (4, 1) и (1, 4). Найдём ситуацию равновесия и средний выигрыш в смешанных стратегиях для этой игры.
Пусть смешанная равновесная стратегия имеет вид X = ( p1, p2 ) = ( p, 1-p )
Найдём значение p из следующего свойства:
Утверждение. Ситуация в смешанных стратегиях является ситуацией равновесия Û ситуация устойчива относительно всех отклонений в чистых стратегиях от этой ситуации.
Смысл утверждения: если первый игрок использует смешанную равновесную стратегию X, то выигрыш второго игрока должен быть одинаковым при любой его стратегии, т.е. выбор стратегии вторым игроком не даёт ему никаких преимуществ. Тогда достаточно обеспечить равенство выигрыша второго игрока при использовании чистых стратегий Y1 = ( 1, 0) и Y2 = ( 0, 1).
Получаем матричное уравнение следующего вида:
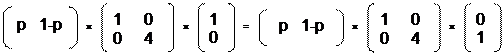 |
X × B × Y1 = X × B × Y2
Подставляем значения X, В, Y1 и Y2, получаем:
Перемножаем, получаем уравнение:
p = 4 – 4p
p = 4/5
Следовательно, смешанная равновесная стратегия первого игрока –- X = (4/5, 1/5).
Аналогичным образом находим равновесную смешанную стратегию для второго игрока. Применение равновесной смешанной стратегии Y = ( q1, q2 ) = (q, 1-q ) должно обеспечивать равный выигрыш первого игрока при использовании чистых стратегий X1 = ( 1, 0) и X2 = ( 0, 1), т.е.
X1 × А × Y = X2 × А × Y
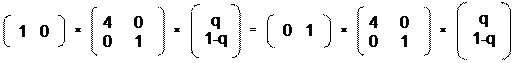 |
Подставляем значения X1, X2, A и Y, получаем:
Перемножаем, получаем уравнение:
4q = 1 – q
q = 1/5
Следовательно, смешанная равновесная стратегия второго игрока - Y = ( 1/5, 4/5).
Определим выигрыш первого и второго игроков при использовании этих равновесных смешанных стратегий:
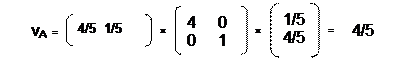 | |
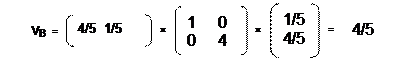 |
Получили ситуацию равновесия в смешанных стратегиях для игры «Семейный спор»: смешанные равновесные стратегии X = (4/5, 1/5) и Y = ( 1/5, 4/5) с выигрышем ( vA , vB ) = ( 4/5, 4/5 ).
Замечание 1: при использовании равновесных смешанных стратегий игроки получили средний выигрыш меньше ( 4/5 < 1 ), чем в ситуациях равновесия в чистых стратегиях (4, 1) и (1, 4), т.к. при случайном выборе стратегий могут встречаться ситуации ( Ф, Т ) и ( Т, Ф ), которые приносят обоим игрокам нулевой выигрыш, за счёт чего средний выигрыш уменьшается.
В биматричной игре «Проникновение на рынок» (из примера 4) не существует ситуации равновесия в чистых стратегиях. Проверьте (аналогично примеру с биматричной игрой «Семейный спор»), что равновесные смешанные стратегии имеют вид X = (2/9, 7/9) и Y = (3/14, 11/14), при этом средний выигрыш игроков ( vA , vB ) = = ( -4/ 7, 3/9 ).
Это означает, что фирма А должна использовать чистые стратегии 1 и 2 с частотами 2/9 и 7/9 , при этом она получит средний выигрыш vA= - 4/7, а фирма В — чистые стратегии 1 и 2 с частотами 3/14 и 11/14, средний выигрыш равен, соответственно, vB = 3/9. При отклонении одной из фирм от указанных смешанных стратегий отклонившаяся фирма уменьшает свой ожидаемый выигрыш.
Замечание 2: использование смешанных стратегий в биматричных играх может как уменьшать ожидаемый выигрыш игроков (например, в игре «Семейный спор»), так и увеличивать его.
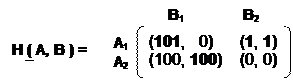 |
Рассмотрим биматричную игру с обобщённой матрицей выигрышей:
В этой игре существует ситуация равновесия в чистых стратегиях ( А1, В2 ) с выигрышем игроков ( 1, 1). Однако, если при повторении игры первый игрок будет с небольшой частотой использовать стратегию А2, то второму игроку будет выгодно от стратегии В2 перейти к стратегии В1, что приведёт к увеличению выигрыша обоих игроков.
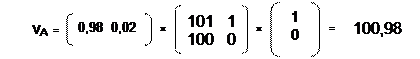 |
Например, если первый игрок будет использовать смешанную стратегию X = (0,98 ; 0,02), а второй игрок – чистую стратегию Y = (1, 0), то их средний выигрыш будет равен:
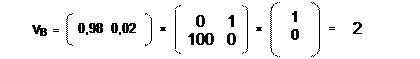 |
Таким образом, использование случайности при выборе стратегии привело к увеличению выигрыша первого игрока более чем в 100 раз и выигрыша второго игрока в 2 раза.
Уменьшение или увеличение выигрыша в биматричных играх при использовании случайного выбора стратегий зависит от условий игры – если игрокам выгоднее договариваться друг с другом (игра «Семейный спор»), то случайность только мешает, если же игроки находятся практически в антагонистических отношениях, то случайность помогает добиться большего выигрыша
Изомерия органических соединений
Изомеры – это соединения с одинаковым элементным составом, но имеющие различный порядок соединения атомов или различное расположение их в пространстве; изомеры отличаются своими физическими и химическими свойствами.
Различаются структурная изомерия и стереоизомерия.
Структурные изомеры – различный порядок соединения атомов.
1) изомерия положения заместителей:
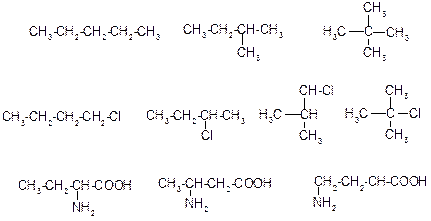
2) изомерия положения кратных связей:
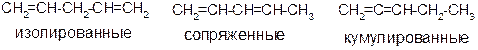
3) межклассовая изомерия:
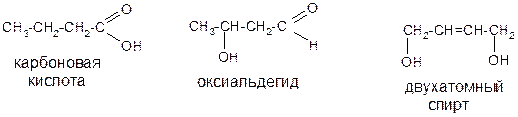
Органические молекулы имеют пространственную трехмерную структуру, и для них возможна пространственная (стерео) изомерия.
Пространственные различия можно разделить на два типа:
1) Конформационные различия, переходящие друг в друга при повороте вокруг химической связи.
2) Конфигурационные различия: их нельзя перевести друг в друга поворотом вокруг связи, для этого необходимо разорвать связи и затем образовать новые.
КОНФОРМАЦИИ
Конформации возникают в результате вращения фрагментов вокруг химических связей и обладают малой устойчивостью, они существуют все вместе: вещество представляет собой смесь молекул в различных конформациях. В любых конформациях сохраняется конфигурационная целостность молекулы. Различные конформации отличаются по термодинамической устойчивости, относительно устойчивые конформации называются конформерами.
Ациклические молекулы
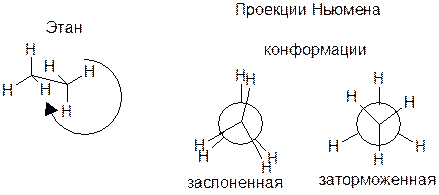
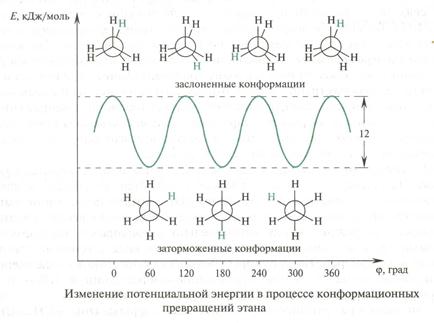
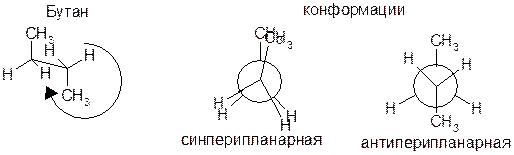
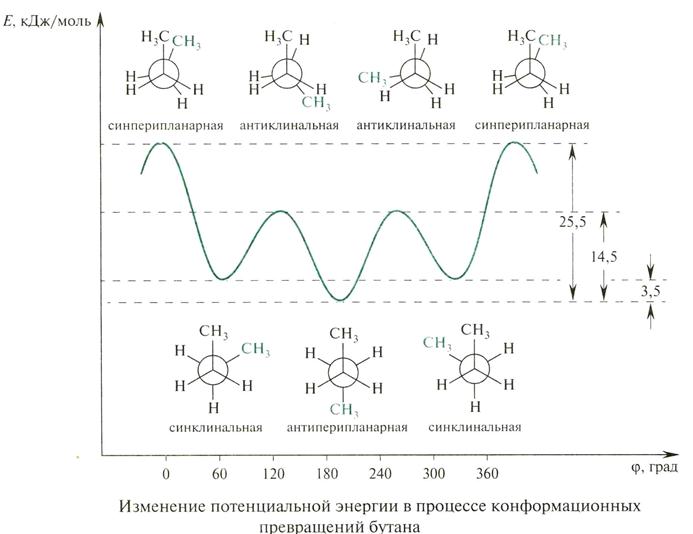
Циклы
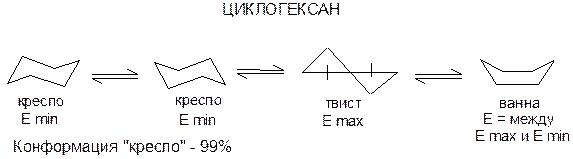
π-Диастереомерия соединений с двойной связью
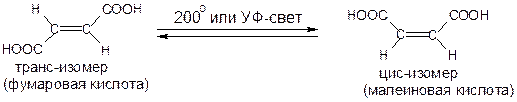
Геометрически цис- и транс-изомеры – это конформации, но устойчивые из-за невозможности свободного вращения вокруг двойной связи.
E,Z-система: Определяется старшинство заместителей попарно. Если оба старших заместителя по одну сторону – это Z-изомер (zusammen), если по разные стороны – это Е-изомер (entgegen):
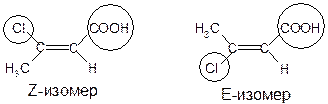
КОНФИГУРАЦИОННАЯ СТЕРЕОИЗОМЕРИЯ
Конфигурация – это порядок соединения атомов, не меняющийся при вращении фрагментов вокруг связи (в отличие от конформации).
Хиральность – это свойства несовместимости предмета с его зеркальным отражением.
Хиральные предметы: рука, буквы и др. Хиральность свойственна и некоторым молекулам:

Атом С – хиральный центр.
Признаки хиральности атома углерода: 1) sp3 гибридизация (тетрагональная геометрическая структура); 2) все четыре заместителя разные.
Отличительное свойство хиральных молекул – оптическая активность (пояснить).
Стереохимическая номенклатура
D,L-система (Розанов, 1906 г.)
Опорное вещество (стандарт Розанова) – глицериновый альдегид. Правовращающему и левовращающему глицериновому альдегиду произвольно приписаны следующие структуры:
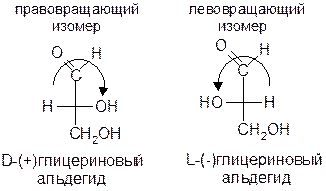
Для других веществ отнесение изомеров произведено путем химических превращений, не затрагивающих хиральный центр. Например, для глицериновой кислоты, полученной окислением глицеринового альдегида:
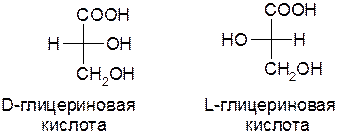
R,S-система (Канн, Ингольд, Прелог, 1951 г.)
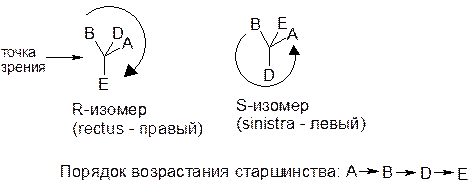
Старшинство определяется порядковым номером элемента, связанного с хиральным центром (неподеленная пара электронов – самая младшая). Например:
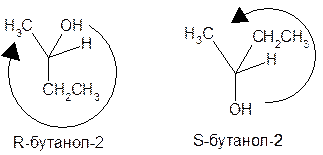
Виды стереоизомеров
Энантиомеры – это соединения, молекулы которых относятся друг к другу как предмет и несовместимое с ним его зеркальное отражение. Энантиомеры отличаются друг от друга только знаком оптической активности, все остальные физические и химические свойства их одинаковы.
Диастереомеры – это стереоизомеры, молекулы которых не относятся друг к другу как предмет и несовместимое с ним его зеркальное отражение. Физические и химические свойства диастереомеров различны. Диастереомерия наблюдается у соединений, имеющих несколько хиральных центров. Общее количество стереоизомеров у таких соединений определяется по формуле: N = n2 (N – общее количество стереоизомеров, n – количество хиральных центров).
Рацемическая смесь (рацемат) – это оптически неактивная смесь равномолярных количеств энантиомеров.
Мезосоединения – это соединения, имеющие хиральные центры, но, в целом, нехиральные и не обладающие оптической активностью.
Примеры:
D-молочная кислота и L-молочная кислота – пара энентиомеров, их равномолярная смесь – рацемат молочной кислоты.
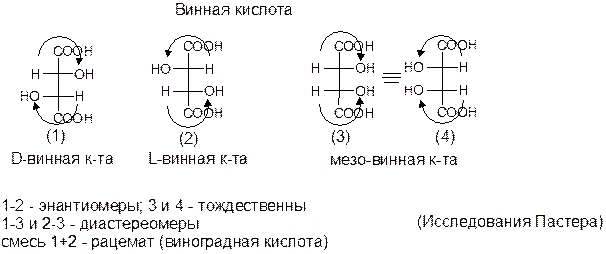
| <== предыдущая страница | | | следующая страница ==> |
| Понятие равновесия по Нэшу. Нахождение ситуации равновесия в биматричных играх | | | Средства обучения изобразительному искусству |
Дата добавления: 2014-07-11; просмотров: 610; Нарушение авторских прав

Мы поможем в написании ваших работ!