
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Пластическое кручение
Увеличивая крутящие моменты мы переводим стержень в пластическое состояние. Считая гипотезу Сен-Венана о том, что сечения остаются плоскими, справедливой, получаем, что отличны от нуля только напряжения 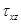 и
и 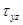 . Эти
. Эти
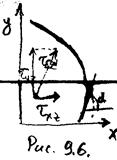
| напряжения, а также контур, изображены на рис.9.6. Будем предполагать идеальную пластичность материала. Условие пластичности запишется в виде: 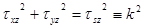 . Распишем компоненты касательного напряжения через угол . Распишем компоненты касательного напряжения через угол 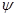 (см. рис.9.6): (см. рис.9.6): 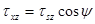 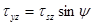 .
Уравнения равновесия должны выполнятся вне зависимости от того находится ли материал в упругом или пластическом .
Уравнения равновесия должны выполнятся вне зависимости от того находится ли материал в упругом или пластическом
|
состоянии, поэтому из формулы ((7.3)л.9) следует:  . Таким образом для одной неизвестной функции имеется одно уравнение. Уравнения характеристик для него:
. Таким образом для одной неизвестной функции имеется одно уравнение. Уравнения характеристик для него: 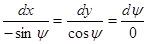 , откуда получаем направления характеристик:
, откуда получаем направления характеристик: 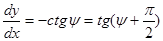 . Отсюда видно, что характеристики перпендикулярны полному вектору напряжений.
. Отсюда видно, что характеристики перпендикулярны полному вектору напряжений.
Интегрируя последнее равенство, получаем: 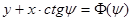 ((7.10)л.9).
((7.10)л.9).
Остается найти функцию 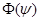 . Обозначим, как и раньше, угол между касательной к контуру и осью x буквой
. Обозначим, как и раньше, угол между касательной к контуру и осью x буквой 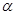 . Тогда, как было показано выше,
. Тогда, как было показано выше, 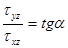 . С другой стороны, по определению угла
. С другой стороны, по определению угла 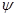 ,
, 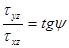 . Следовательно
. Следовательно 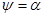 . Если контур задан с помощью функций от
. Если контур задан с помощью функций от 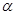 как
как  ,
, 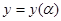 , то функция
, то функция 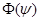 имеет вид:
имеет вид: 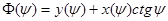 ((7.11)л.9).
((7.11)л.9).
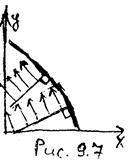
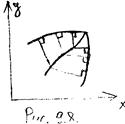
| Картина напряжений в пластическом случае изображена на рис.9.7: касательные напряжения перпендикулярны нормали к контуру (т.е. параллельны касательным). В силу того, что материал находится в пластическом состоянии, они равны по величине. Подобные рассуждения проходят в случае гладкого контура. Однако, контур не обязан быть гладким. Рассмотрим контур, изображенный на рис.9.8. Как и в предыдущем случае, построим нормали к контуру, они будут пересекаться и множество точек их пересечения будет образовывать целую линию. Эта линия является областью неоднозначности, так как в каждой ее точке напряжения имеют два различных направления, что физически невозможно. Чтобы выйти из создавшегося положения, введем линии разрыва напряжений. |
| <== предыдущая страница | | | следующая страница ==> |
| Теорема о разгрузке | | | Великая Отечественная война 1941 – 1945 гг |
Дата добавления: 2014-07-11; просмотров: 295; Нарушение авторских прав

Мы поможем в написании ваших работ!