
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Теорема о разгрузке
При капитальном ремонте и реконструкции решаются вопросы усиления и уширения дорожных одежд. Дорожную одежду можно усилить, как без уширения, так и с уширением проезжей части. Уширение чаще всего совмещают с усилением дорожной одежды. Возможны три основных способа повышения ее прочности: строительство покрытия на старой дорожной одежде; замена верхнего слоя или всех слоев покрытия с сохранением или с усилением основания; полная замена всей дорожной одежды с учетом перспективы роста интенсивности движения.
Первый способ по сравнению с другими требует меньших первоначальных затрат, но применим он, когда недостаточная прочность дорожной одежды связана с частичной потерей прочности материалов или слоев покрытия. Перед укладкой на старое покрытие асфальтобетона, его армируют синтетическим материалом. В Англии разработан материал в виде решетки из высокопрочных полимеров, который равномернее распределяют нагрузку на нижележащие слои, воспринимает растягивающие и напряжения и локаризует развитие трещин (рисунок 4.5). Этот материал позволяет экономить до 25% смеси при усилении асфальтобетонных покрытий. Аналогичная конструкция разработана в Хабаровском филиале Гипродорнии.
Локализация трещин в дорожной одежде при укладке решетки из синтетического материала

а) общий вид материала Tensar; б) -дорожная одежда без прокладки; в) тоже с прокладкой.
Второй способ состоит в замене верхнего слоя и всех слоев покрытия с сохранением существующего основания дорожной одежды. Его применяют, если на старом покрытии много повреждений в виде сетки трещин и выбоин, связанных с существенной потерей прочности материала покрытия или его слоев. Кроме того, этот способ целесообразен в тех местах, где нельзя увеличивать толщину покрытия (например, на мостах во избежание снижения их грузоподъемности, в тоннелях и на участках под путепроводами, во избежание уменьшения габаритов по высоте). Асфальтобетонные слои снимают с помощью фрез.
Третий способ предусматривает полную замену всей дорожной одежды. Это может потребоваться при потере прочности материалов или слоев основания, необходимости строительства новых дополнительных слоев основания (дренирующего, теплоизолирующего), а также исправлении земляного полотна. В каждом случае рекомендуется максимально использовать материал старой дорожной одежды.
Возможны два варианта уширения дорожной одежды: одностороннее (несимметричное) и двухстороннее. При одностороннем уширении дорожной одежды, как правило, устраивают выравнивающий слой и новое покрытие на всю ширину проезжей части.
Схемы уширения дорожной одежды

О-О – старая ось дорожной одежды; I-I – новая ось; 1 - верхний слой нового покрытия; 2 – выравнивающий слой; 3 – верхний слой старого покрытия и продолжение его на уширении; 4 – нижний слой старого покрытия; 5 – основание; 6 – дополнительный слой основания; 7 – уступы.
Двустореннее уширение может быть выполнено двумя способами:
-устройством полос уширения доржной одежды на уширенном с двух сторон земляном полотне,
-уширение проезжей части на ширину, в 2 раза меньшую ширины обочины, или на ширину краевых укрепленных полос (т.е. с каждой стороны на 0,25-0,75 м) без уширения земляного полотна
В первом случае на обочине вдоль кромки покрытия подготавливают
корыто до низа дополнительного слоя основания (дренирующего или морозозащитного). Дну корыто придают поперечный уклон 30-120 ‰ в сторону обочины, чтобы обеспечить водоотвод из основания. При устройстве полос малой ширины (0,25-0,75 м) применяют траншеекопатели и приспособления к машинам, в том числе навесные и прицепные плуги, накладки на отвал.
Технологический процесс устройства дорожной одежды на полосах уширения включает обрезку кромки покрытия с помощью дисковых пил, навешиваемых на трактор, послойную отсыпку основания с тщательным уплотнением каждого слоя, строительство покрытия. На полосах уширения при необходимости устраивают поверхностную обработку, захватывая на 0,2-0,3 м прикромочную полосу старого покрытия. Поверхностную обработку целесообразно устраивать сразу на всю ширину, перекрывая старое покрытие и полосы уширения.
Во втором случае после уширения и уплотнения земляного полотна до нижней поверхности дополнительного слоя основания (дренирующего или морозозащитного) отсыпают материал для уширения основания, затем укладывают и уплотняют его и вровень с ним отсыпают и уплотняют грунт в пределах образуемой новой обочины. После этого укладывают выравнивающий слой (при необходимости), а поверх него новый верхний слой покрытия на всю ширину проезжей части. Затем укрепляют обочины и окончательно отделывают земляное полотно.
Теорема о разгрузке.
Итак, рассмотрен ряд теорий о поведении материала за пределами упругости. Теперь обратимся к другому вопросу: что будет, если начать разгружать образец, который уже находится в пластическом состоянии?
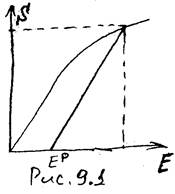
| Обратимся к эксперименту. Будем рассматривать диаграмму нагружения материала, обладающего упрочнением (рис.9.1). Разгрузка идет по линейному закону, причем угол наклона участка разгрузки совпадает с углом наклона упругого участка- это экспериментально установленный факт. В начальный момент времени упруго-пластическая задача решена, то есть найдены шесть компонент тензора напряжений 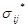 , шесть компонент тензора деформаций , шесть компонент тензора деформаций 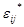 и три компоненты вектора и три компоненты вектора
|
смещений 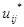 . В этот же момент начинается разгрузка. Напряжения, деформации и перемещения естественно начнут изменяться, но они должны удовлетворять пятнадцати уравнениям: трем уравнениям равновесия
. В этот же момент начинается разгрузка. Напряжения, деформации и перемещения естественно начнут изменяться, но они должны удовлетворять пятнадцати уравнениям: трем уравнениям равновесия 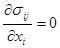 , шести уравнениям, связывающим деформации с перемещениями и шести- связывающим напряжения с деформациями. Краевые условия для уравнения равновесия заданы в напряжениях следующим образом:
, шести уравнениям, связывающим деформации с перемещениями и шести- связывающим напряжения с деформациями. Краевые условия для уравнения равновесия заданы в напряжениях следующим образом: 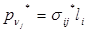 , где
, где 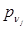 - проекции внешних напряжений на соответствующие оси в начальный момент времени, а
- проекции внешних напряжений на соответствующие оси в начальный момент времени, а 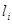 - направляющие косинусы нормали к поверхности. Предположим, что разгрузка ведется по закону
- направляющие косинусы нормали к поверхности. Предположим, что разгрузка ведется по закону 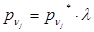 , где
, где 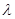 - параметр, изменяющийся во времени в пределах от единицы до нуля, причем
- параметр, изменяющийся во времени в пределах от единицы до нуля, причем 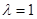 - соответствует началу процесса, а
- соответствует началу процесса, а 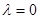 - полной разгрузке.
- полной разгрузке.
Символами без звездочки ( 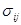 ,
, 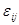 ,
, 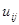 ) будем обозначать текущие значения величин, характеризующих напряженное состояние. Они должны удовлетворять уравнениям равновесия и краевым условиям. А каким условиям связи между напряжениями и деформациями они должны удовлетворять? Эксперимент гласит, что эта связь должна быть подобна связи в упругой области.
) будем обозначать текущие значения величин, характеризующих напряженное состояние. Они должны удовлетворять уравнениям равновесия и краевым условиям. А каким условиям связи между напряжениями и деформациями они должны удовлетворять? Эксперимент гласит, что эта связь должна быть подобна связи в упругой области.
Введем величину 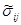 следующим образом:
следующим образом: 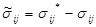 , т.е. это разность между начальными и текущими напряжениями. Так как
, т.е. это разность между начальными и текущими напряжениями. Так как 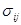 и
и 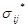 удовлетворяют уравнениям равновесия, то ему удовлетворяет и
удовлетворяют уравнениям равновесия, то ему удовлетворяет и 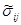 , т.е.
, т.е. 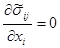 . Кроме того очевидна справедливость и такого равенства:
. Кроме того очевидна справедливость и такого равенства: 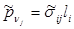 , где
, где 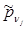 вводится аналогично
вводится аналогично 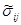 . Так же обозначим и разность деформаций:
. Так же обозначим и разность деформаций: 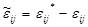 . Построенные разности удовлетворяют закону Гука:
. Построенные разности удовлетворяют закону Гука: 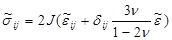 . Таким образом, для разностей получена упругая задача, которую уже можно решить, то есть можно найти все величины с волной. Итак, известны разности начальных и текущих значений, известны начальные значения, следовательно в каждый момент времени известны деформации, напряжения и смещения.
. Таким образом, для разностей получена упругая задача, которую уже можно решить, то есть можно найти все величины с волной. Итак, известны разности начальных и текущих значений, известны начальные значения, следовательно в каждый момент времени известны деформации, напряжения и смещения.
Остается последний вопрос: что произойдет при полной разгрузке?
В этот момент 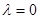 , следовательно
, следовательно 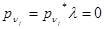 . Для разности:
. Для разности: 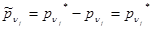 . Как показывает опыт, в теле остаются некие остаточные деформации
. Как показывает опыт, в теле остаются некие остаточные деформации 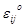 и, следовательно, напряжения
и, следовательно, напряжения 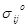 . При полной разгрузке выполняются условия:
. При полной разгрузке выполняются условия: 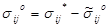 и
и 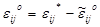 . Таким образом для нахождения остаточных напряжений и деформаций надо решить упруго-пластическую задачу (т.е. определить величины со звездочкой) и решить фиктивно упругую задачу (для нахождения
. Таким образом для нахождения остаточных напряжений и деформаций надо решить упруго-пластическую задачу (т.е. определить величины со звездочкой) и решить фиктивно упругую задачу (для нахождения 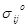 и
и 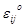 ).
).
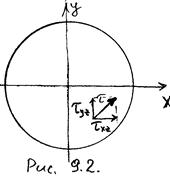
| Упруго-пластическое кручение.
Стержень круглого сечения нагружен некоторым крутящим моментом. Ось стержня параллельна оси z. Вследствие нагружения в сечении стержня возникают напряжения 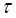 с компонентами с компонентами 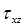 и и 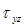 (см. рис. 9.2). Предположим следующее поведение сечений стержня: сечения поворачиваются одно относительно другого как твердые тела, однако при этом не остаются плоскими, т.е. существуют ненулевые смещения вдоль оси z: (см. рис. 9.2). Предположим следующее поведение сечений стержня: сечения поворачиваются одно относительно другого как твердые тела, однако при этом не остаются плоскими, т.е. существуют ненулевые смещения вдоль оси z: 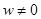 . Эти предположения могут быть . Эти предположения могут быть
|
записаны в следующем виде: 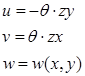 ((7.1)л.9), где
((7.1)л.9), где 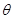 - крутка, т.е. угол поворота единицы длины стержня.
- крутка, т.е. угол поворота единицы длины стержня.
Допустим, мы каким-то образом нанесли на сечение координатную сетку. Как она деформируется при указанном выше нагружении стержня? Она повернется, не деформируясь. Действительно, растяжения отрезков, параллельных соответствующим осям отсутствуют: 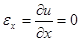 ,
, 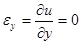 ,
, 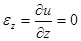 . Кроме того, не изменятся и углы сетки, в силу того, что
. Кроме того, не изменятся и углы сетки, в силу того, что 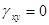 .
.
Итак, в тензоре деформаций остается только две компоненты:
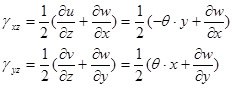 ((7.2)л.9)
((7.2)л.9)
Зная деформации, из закона Гука получаем, что 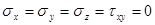 . Из трех уравнений равновесия Коши, первые два выполняются тождественно, в последнем же остается только два слагаемых:
. Из трех уравнений равновесия Коши, первые два выполняются тождественно, в последнем же остается только два слагаемых:
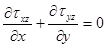 ((7.3)л.9).
((7.3)л.9).
Два слагаемых останется и в выражении для квадрата интенсивности касательных напряжений:
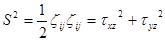 ((7.4)л.9).
((7.4)л.9).
Таким образом, имеется две неизвестных функции 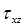 и
и 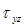 , и одно уравнение для их определения. Введем новую функцию
, и одно уравнение для их определения. Введем новую функцию 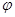 по следующему правилу:
по следующему правилу: 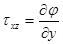 ,
, 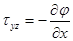 ; тогда уравнение ((7.3)л.9) удовлетворяется тождественно. Если первое уравнение из ((7.2)л.9) продифференцировать по y, а второе- по x и вычесть из первого, то получится:
; тогда уравнение ((7.3)л.9) удовлетворяется тождественно. Если первое уравнение из ((7.2)л.9) продифференцировать по y, а второе- по x и вычесть из первого, то получится:
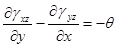 ((7.2’)л.9)
((7.2’)л.9)
С другой стороны, из закона Гука, следует, что 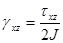 и
и 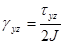 . Выражая напряжения
. Выражая напряжения 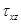 и
и 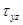 через введенную выше функцию
через введенную выше функцию 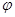 и подставляя в ((7.2’)л.9), получаем:
и подставляя в ((7.2’)л.9), получаем:
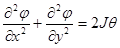 , ((7.5)л.9)
, ((7.5)л.9)
то есть уравнение Пуассона.
Кроме уравнения необходимы и граничные условия. Как уже неоднократно говорилось, для уравнений равновесия такими условиями являются поверхностные напряжения: 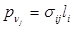 . В нашем случае в тензоре напряжений только две ненулевые компоненты, и, кроме того, на поверхности цилиндра не действуют никакие напряжения, поэтому условие перепишется в виде:
. В нашем случае в тензоре напряжений только две ненулевые компоненты, и, кроме того, на поверхности цилиндра не действуют никакие напряжения, поэтому условие перепишется в виде:
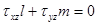 ((7.6)л.9).
((7.6)л.9).
Напомним, что 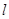 - это косинус угла между нормалью к поверхности стержня и осью x,
- это косинус угла между нормалью к поверхности стержня и осью x, 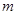 - то же для оси y.
- то же для оси y.
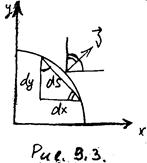
| Выразим направляющие косинусы через дифференциалы дуги (см. рис. 9.3): 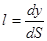 , , 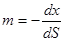 . Подставим выраженные таким образом косинусы в формулу ((7.6)л.9), а также заменим в ней напряжения через производные от функции . Подставим выраженные таким образом косинусы в формулу ((7.6)л.9), а также заменим в ней напряжения через производные от функции 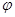 : :
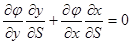
|
Последнее равенство утверждает, что приращение функции 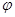 вдоль направления, заданного дифференциалами dx и dy (т.е. вдоль контура), равно нулю, следовательно на контуре
вдоль направления, заданного дифференциалами dx и dy (т.е. вдоль контура), равно нулю, следовательно на контуре 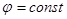 . Положим эту константу равной нулю (отметим, что это можно сделать лишь в случае односвязного контура). В результате на функцию
. Положим эту константу равной нулю (отметим, что это можно сделать лишь в случае односвязного контура). В результате на функцию 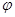 получена задача Дирихле для уравнения Пуассона:
получена задача Дирихле для уравнения Пуассона:
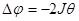 , ((7.7)л.9)
, ((7.7)л.9)
граничное условие 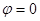 .
.
Если относительный поворот крайних сечений стержня составляет угол 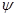 , а полная длина стержня
, а полная длина стержня 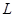 , то крутка
, то крутка 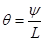 . Остается связать заданную величину приложенного к стержню момента
. Остается связать заданную величину приложенного к стержню момента 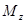 и крутку
и крутку 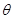 .
.
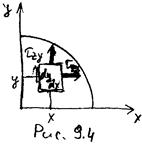
| Из рис.9.4 легко понять, что момент, приложенный к малому элементу сечения есть: 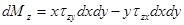 . Интегрируя по всей площади сечения, получаем: . Интегрируя по всей площади сечения, получаем: 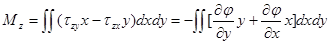 . Далее интегрируем по частям: . Далее интегрируем по частям:
|
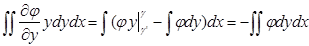 , проинтегрированная
, проинтегрированная
часть зануляется в силу того, что на границе области 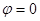 . Проведя аналогичную операцию со вторым слагаемым получим:
. Проведя аналогичную операцию со вторым слагаемым получим:
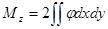 . ((7.8)л.9).
. ((7.8)л.9).
Требуемая связь получена: решая задачу Дирихле находим связь между 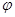 и
и 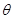 , а формула ((7.8)л.9) связывает известную величину
, а формула ((7.8)л.9) связывает известную величину 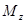 и
и 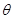 . Таким образом задача полностью решена.
. Таким образом задача полностью решена.
Отметим, что так как нормальные составляющие напряжений на поверхности равны нулю, то справедливо равенство:
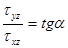 , ((7.9)л.9)
, ((7.9)л.9)
где 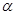 - угол между касательной к поверхности стержня и осью x (рис 9.5).
- угол между касательной к поверхности стержня и осью x (рис 9.5).
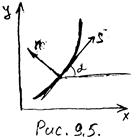
| Эта формула утверждает, что касательные напряжения параллельны касательной к контуру. Обоснуем ее: выберем новую систему координат s, n (рис.9.5) и введем функцию 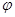 в этой системе: в этой системе: 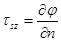 , , 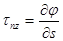 , а так как , а так как 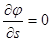 , т.е. , т.е. 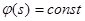 на контуре, то на контуре, то 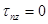 , что и , что и
|
приводит к формуле ((7.9)л.9).
| <== предыдущая страница | | | следующая страница ==> |
| Капитальный ремонт щебеночных (гравийных), асфальтобетонных и цементобетонных покрытий | | | Пластическое кручение |
Дата добавления: 2014-07-11; просмотров: 510; Нарушение авторских прав

Мы поможем в написании ваших работ!