
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Кинематическая теория дифракционного контраста
Модель кодирования RGB (Red. Green. Blue)
Красный. Зеленый. Синий
Модель RGB используется в мониторах, телевизорах, проекторах, сканерах, цифровых фотоаппаратах.
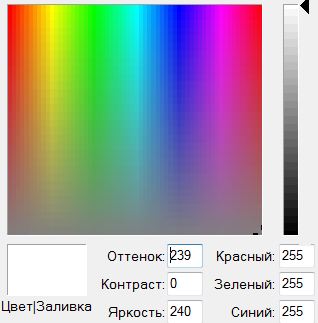
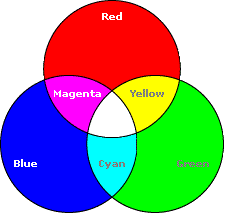

Основные цвета:
Красный (255,0,0)
Зеленый (0,255,0)
Синий (0,0,255)
Дополнительные цвета:
Голубой (0,255,255)
Лиловый (255,0,255)
Желтый (255,255,0)
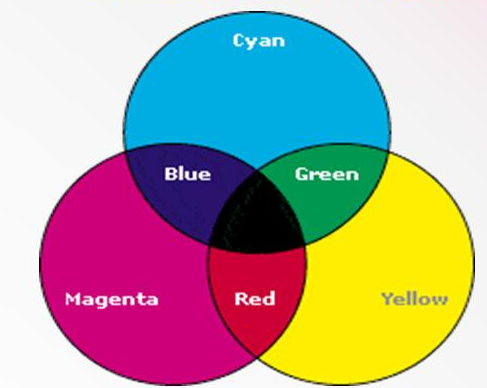
Модель кодирования CMYK (Cyan. Magenta. Yellow. Black)
Голубой. Лиловый. Желтый. Черный.
Модель CMYK используется в полиграфии.
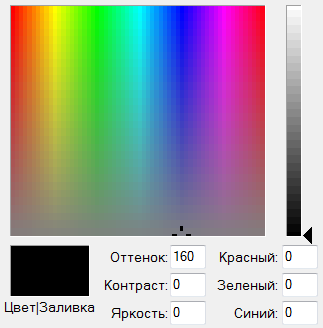
Модель кодирования HSB
Модель HSB характеризуется тремя компонентами: оттенок цвета (Hue), насыщенность цвета (Saturation) и яркость цвета (Brightness). Можно получить большое количество произвольных цветов, регулируя эти компоненты. Эту цветовую модель лучше применять в тех графических редакторах, в которых изображения создают сами, а не обрабатывают уже готовые.
2. Векторная графика -графические объекты создаются как совокупности линий, векторов, точек.
С их помощью можно создавать сложные и красивые изображения, которые носят несколько искусственный характер. Используются при создании рекламных объявлений, технических иллюстраций – там, где не требуется фотореалистичность изображений.
Не пригодна для создания художественных иллюстраций.
Достоинства:
-изображение занимает меньший объем памяти по сравнению с растровым.
-качество изображения не ухудшается при увеличении масштаба.
Кодирование видео данных.
Каждый кадр – это графические данные.
Например: байт 11000001 (193) -светло-серая точка.
Структуры данных.
При составлении компьютерных программ, предназначенных для обработки больших массивов данных важно, чтобы эти данные были упорядочены.
Для этого применяются следующие структуры данных.
1. Массив данных – он может иметь линейную или табличную структуру.
Линейная структура (список) – это упорядоченная структура, в которой адрес данного определяется его номером (индексом).
| А(1) Иванов | А(2) Петров | А(3) Сидоров | А(4) Орлов |
Табличная структура данных – это упорядоченная структура, в которой адрес данного определяется двумя числами - номером строки и номером столбца на пересечении которых находится ячейка с искомым элементом.
| Х(1,1) | Х(1,2) | Х(1,3) 7,2 | Х(1,4) |
| Х(2,1) | Х(2,2) | Х(2,3) | Х(2,4) |
| Х(3,1) | Х(3,2) | Х(3,3) | Х(3,4) |
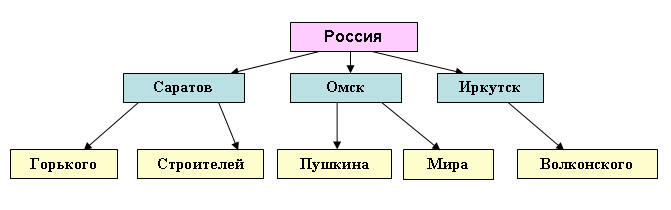
2.Иерархическая структура (дерево) – в ней адрес каждого элемента определяется маршрутом доступа (указывается путь).
Россия\Омск\Пушкина\д.5
Введение нового элемента не нарушает структуры дерева.
Хранение данных.
При хранении данных решается две задачи:
-как сохранить данные;
-как обеспечить быстрый удобный доступ к ним.
Единицей хранения данных является объект переменной длины, называемый файлом.
Файл - поименованная последовательность байтов, записанная на жесткий или гибкий магнитный диск.
В файлах могут храниться тексты программ, документы, готовые к выполнению программы и любые другие данные.
Имена файлов.
В имени файла можно использовать не более 256 символов.
У имени может быть расширение, в котором хранятся сведения о типе данных (текстовые, графические, звуковые).
По расширению можно определить с помощью какой программы файл был создан.
Расширение начинается с точки, за которой следуют от 1 до 4 символов.
Примеры имен файлов с различными расширениями.
Файлы, в которых содержатся программы, записанные машинными двоичными кодами.
| Statist.exe | компьютерная программа, которую можно запускать |
| Command.com | программа служебного назначения |
Файлы, которые можно только открывать, читать, просматривать и записывать, но нельзя запускать.
| Paper.doc | файл, созданный текстовым редактором Word |
| Флаг.jpg | файл, созданный графическим редактором Paint |
| Таблица 1.xls | файл, созданный в табличном процессоре Excel |
| Вальс.wav | музыкальный файл |
| Зоопарк.avi | файл, содержащий видеоролик |
| Tb.rar | архивный файл |
| Tb.hlp | справочный файл |
| Statist.bas | текст программы, записанной на языке программирования Basic |
Форматы растровых графических файлов
BMP – формат рисунков. Его можно использовать для хранения нарисованных Вами рисунков на компьютере. В Интернете этот формат не используется из-за его большого объема. Если Вы хотите свой рисунок «вывесить» на форум или в социальную сеть, формат должен быть gif, jpg или png.
GIF – популярный формат рисунков. В нем можно сохранять рисунки без потери качества, но с ограниченным количеством цветов – 256. Этот формат очень распространен в Интернете, в нем создаются небольшие анимированные (движущиеся) картинки.
JPG – формат фотографий и картин с большим количеством цветов. В этом формате можно сохранить изображение как без потери качества, так и с её потерей.
PNG – современный формат рисунков. Изображение в таком формате получается небольшого размера без потери качества.
TIFF – формат изображений очень хорошего качества (без сжатия). И, соответственно, размер у таких изображений огромный. Этот формат используют тогда, когда качество имеет большое значение.
Форматы векторных графических файлов
WMF - используется для хранения коллекции графических изображений Microsoft Clip Gallery. Основные недостатки - искажение цвета, невозможность сохранения ряда дополнительных параметров объектов.
CGM -использует стандартный формат векторных графических данных в сети Internet.
CDR -используется в векторном графическом редакторе Corel Draw.
Кинематическая теория дифракционного контраста.
Дифракционная электронная микроскопия включает совокупность экспериментальных и теоретических приемов получения, расчета и толкования электронных изображений и микродифракционных картин. При использовании данных о кристаллографии объекта и привлечении выводов теории дефектов в кристаллах это позволяет предсказать контраст в определенных условиях дифракции и сопоставив его с наблюдаемым, сделать выводы о характере реальной структуры объекта.
Рассмотрим подробнее механизм возникновения дифракционного контраста. Для простоты п роследим сначала контраст на темнопольном изображении. Рассмотрение контраста в кинематическом приближении без учета поглощения ограничи- вается тонкими кристаллами при достаточно больших отклонениях плоскостей, дающих рассматриваемое отражение, от брегговского положения, когда отраженный пучок существенно слабее первичного.
Контраст, как было показано выше, определяется распределением локальных условий дифракции. Рассмотрим степень влияния условий дифракции на локальное распределение интенсивности на выходе из кристалла, то есть в плоскости объекта (2), сопряженной с плоскостью (5) (см. рис.6). Разберем простейший случай. Пусть на электронограмме путем со-ответствующих поворотов монокристаллического образца остается кроме нулевого еще один рефлекс, отражение от остальных плоскостей существенно слабее. Поэтому при качественном рассмотрении контраста в дальнейшем ограничимся так называемым двухлучевым приближением. При этом полагаем ,что дифракционный контраст формируется за счет отражения только от одной системы плоскостей. Интенсивность, отраженную остальными плоскостями считам пренебрежимо малой. В двухлучевом приближении в точку Р (рис.8а) приходят потоки энергии в угловом интервале не большем, чем 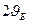 . Это отвечает поверхности, лежащей между точками АВ. Колонковое приближение состоит в том, что условия дифракции внутри колонки сечением АВ определяет интенсивность дифрагированных пучков (темнопольное изображение) или прошедших (светлопольное), которая не зависит от условий дифракции вне этой колонки.Так при толщине фольги ~100 нм и
. Это отвечает поверхности, лежащей между точками АВ. Колонковое приближение состоит в том, что условия дифракции внутри колонки сечением АВ определяет интенсивность дифрагированных пучков (темнопольное изображение) или прошедших (светлопольное), которая не зависит от условий дифракции вне этой колонки.Так при толщине фольги ~100 нм и  рад размер АВ
рад размер АВ 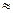 1 нм. Это дает основание разбить кристалл на колонки диаметром АВ
1 нм. Это дает основание разбить кристалл на колонки диаметром АВ  и рассматривать распределение интенсивности в сечении освещенной части образца, как распределение, отвечающее условиям дифракции в отдельных колонках. При этом допускают, что условия дифракции в сечении каждой колонки одинаковы для всего сечения и могут изменяться лишь вдоль оси колонки.
и рассматривать распределение интенсивности в сечении освещенной части образца, как распределение, отвечающее условиям дифракции в отдельных колонках. При этом допускают, что условия дифракции в сечении каждой колонки одинаковы для всего сечения и могут изменяться лишь вдоль оси колонки.
Возможен другой подход. Пусть волна, отраженная от какой либо системы плосктей, почти перпендикулярной поверхности образца, попадает в точку Р на нижней поверхности образца (рис.8 б). Для расчета контраста необходимо оценить с какого участка образца изллучение приходит в эту точку. Разделим кристалл на ряд слоев, параллельных поверхности. Воспользуемся построением Френеля для волны, рассеивающейся на слоях и распространяющейся вдоль ОР. Допустим, что практически весь вклад в амплитуду этой волны определяется первыми десятью зонами Френеля. При толщине фольги X ~100 нм первые десять зон для верхнего слоя можно оценить следующим образом. Радиус первой зоны
 ,
,
где  - длина волны, Х- расстояние от верхнего слоя до точки Р.
- длина волны, Х- расстояние от верхнего слоя до точки Р.
Радиус первых десяти зон равен 3R. При длине волны при рабочем напряжении 200 кВ равной 0,0025 нм радиус десяти зон равен 3R=1,5 нм. Выделим в фольге цилиндрическую колонку радиусом 3R c осью, проходящей через точку Р. Так как углы дифракции малы, то длина колонки приблизитель-но равна толщине фольги. Амплитуда волны в точке Р определяется только излучением, рассеянным кристаллическим объемом, лежащим внутри этой колонки, и не зависит от условий дифракции в соседних колонках. И в первом и во втором случаях независимо от подхода, очевидно, что при анализе контраста можно рассматривать интенсивности дифрагированных пучков в отдельных колонках. Поскольку полагают, что в сечении колонки условия дифракции одинаковы, очевидно, для расчета амплитуд можно рассматривать в каждой колонке столбик ячеек, длине колонки.
При симметричной дифракции электронов по схеме Лауэ в непоглощающей фольге толщиной Х интенсивность дифрагированной волны описывается формулой
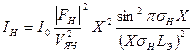 , (4)
, (4)
где 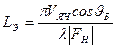 - экстинкционная длина;
- экстинкционная длина;
 - обратная экстинкционная длина;
- обратная экстинкционная длина;
s-вектор, характеризующий отклонение отражающих плоскостей от брегговского положения.
Для тонкой фольги вектор s перпендикулярен ее плоскости и параллелен Х. При s=0
IH~sin2( 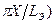 .
.
Если sLЭ>>1, то выражение принимает вид:
IH=I0 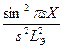 , (4а)
, (4а)
что с точностью до константы совпадает с формулой, справедливой в кинематическом приближении. Используя формулы (4) можно вычислить амплитуды пучков дифрагированных и прошедших Iсветл.=I0-IH в каждой колонке совершенного не поглощающего кристаллафольги. Отсюда очевидно, что контраст на светлопольном и темнопольном изображениях в двухлучевом приближении, если не учитывать поглощения, является взаимно обратным или взаимно дополняющим. Для качественного анализа контраста удобно пользоваться формулой (4а). В частности, зависимость величины амплитуды дифрагированной волны от условий дифракции (Х и s) хорошо иллюстрируется с помощью амплитудно фазовой диаграмы. Пусть имеется колонка длиной Х. Если все элементы колонки рассеивают в олной фазе (s=0), то амплитуда пропорциональна длине колонки Х (рис.9 а). Если условия дифракции таковы, что вектор s не равен нулю, то элементы колонки на расстоянии dx рассеивают с разницей фаз  .В этом случае амплитудно-фазовая диаграмма, изображающая сумму всех элементов dx, представляет окружность радиусом
.В этом случае амплитудно-фазовая диаграмма, изображающая сумму всех элементов dx, представляет окружность радиусом 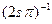 или ее часть в зависимости от длины колонки Х и величины s . Результирующая амплитуда изобразится отрезком ОР1. Длина этого отрезка в соответствии с (4а) равна
или ее часть в зависимости от длины колонки Х и величины s . Результирующая амплитуда изобразится отрезком ОР1. Длина этого отрезка в соответствии с (4а) равна  . Рассмотрим два простейших примера. Пусть есть в фольге два рядом расположенных зерна-кристаллита. Вследствие изменения ориентации решетки при переходе от одного зерна к другому аплиту ды дифрагированных пучков из за разных значений параметра s различны. Соответственно освещенность изображений зерен разная. На участке, соответствующем изображению высокоугловой границы этих зерен, получим систему темно-белых полос, параллельных линии пересечения границы зерен с поверхностью фольги. Положим для простоты, что амплитуда дифрагированного пучка в первом зерне сущкственно больше, чем во втором. Тогда контраст на границе определяется дифракцие только в первом зерне, край которого представляет для наклонной границы клин (рис.10). В этом случае для колонок разной длины амплитуда в соответствии с формулой (4а) осциллирует. Эпитаксиальные слои часто содержат микродвойники. На изображениях фольги двойники имеют вид прямых пластин с периодическим контрастом по краям, обусловленным переменной толщиной матрицы при наклонном расположении двойниковой пластинки.
. Рассмотрим два простейших примера. Пусть есть в фольге два рядом расположенных зерна-кристаллита. Вследствие изменения ориентации решетки при переходе от одного зерна к другому аплиту ды дифрагированных пучков из за разных значений параметра s различны. Соответственно освещенность изображений зерен разная. На участке, соответствующем изображению высокоугловой границы этих зерен, получим систему темно-белых полос, параллельных линии пересечения границы зерен с поверхностью фольги. Положим для простоты, что амплитуда дифрагированного пучка в первом зерне сущкственно больше, чем во втором. Тогда контраст на границе определяется дифракцие только в первом зерне, край которого представляет для наклонной границы клин (рис.10). В этом случае для колонок разной длины амплитуда в соответствии с формулой (4а) осциллирует. Эпитаксиальные слои часто содержат микродвойники. На изображениях фольги двойники имеют вид прямых пластин с периодическим контрастом по краям, обусловленным переменной толщиной матрицы при наклонном расположении двойниковой пластинки.
Другой пример. Пусть участок исследуемой фольги имеет постоянную толщину, но разную локальную ориентацию (параметр s из-за изгиба фольги меняется). С ее изменением изменяется радиус окружности амплитудно-фазовой диаграммы, и в соответствии с формулой (4а) меняется амплитуда. Это вызывает появление так называемых изгибных или экстинкционных контуров. Основной контур возникает в тех участках кристалла где s=0. При определенных условиях, если позволяет расходимость пучка, на экстинкционном контуре может наблюдаться тонкая структура, то есть могут быть видны дополнительные параллельные контуры, отвечающие дополнительным максимумам функции  . По расстоянию между ними можно определять толщину фольги. При покачивании образца изгибные контуры перемещаются через поле зрения.
. По расстоянию между ними можно определять толщину фольги. При покачивании образца изгибные контуры перемещаются через поле зрения.
Дифракционный контраст в несовершенных кристаллах (кинематическое приближение).
Контраст, связанный с особенностями микроструктуры несовершенных кристаллов, возникает из-за локальных изменений условий дифракции, вызванных различного рода несовершенствами .Влияние дефектов решетки на условия дифракции можно рассматривать с помощью векторов полей смещений ячеек вокруг дефектов. Пусть вектор рассеяния  , вектор, характеризующий положение ячеек в идеальном кристалле
, вектор, характеризующий положение ячеек в идеальном кристалле 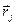 , а вектор
, а вектор 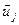 задает смещение j-ой ячейки, определяемое полем смещений дефекта. Тогда для амплитуды волны, рассеянной какой либо колонкой, можно записать:
задает смещение j-ой ячейки, определяемое полем смещений дефекта. Тогда для амплитуды волны, рассеянной какой либо колонкой, можно записать:
 .
.
В колонковом приближении допускается , что величины  и
и 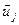 в сечении колонки постоянны и меняются только по длине колонки. Так как
в сечении колонки постоянны и меняются только по длине колонки. Так как 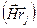 -целое число и
-целое число и  , а суммирование по всем ячейкам колонки можно заменить суммированием по ячейкам столбика из элементарных ячеек параллельного
, а суммирование по всем ячейкам колонки можно заменить суммированием по ячейкам столбика из элементарных ячеек параллельного  ,умножив сумму на число столбиков в сечении колонки – Ns, получим:
,умножив сумму на число столбиков в сечении колонки – Ns, получим:
 .
.
Или, заменив суммирование интегрированием, учитывая, что 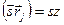 (где z – проекция
(где z – проекция
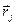 на нормаль к поверхности фольги) приходим к выражению:
на нормаль к поверхности фольги) приходим к выражению:
 , (5)
, (5)
где Z- толщина фольги.
Из формулы (5) видно, что наличие дефекта добавляет дополнительную разницу фаз между волнами рассеянными элементами колонки. Без дефекта эта разница фаз есть  , а дефект добавляет еще
, а дефект добавляет еще  . В результате в подинтегральном выражении появляется множитель
. В результате в подинтегральном выражении появляется множитель  , влияющий на амплитуду дифрагированной волны, следовательно, на контраст. Удобно фазовый множитель представить в иной форме. Учитывая очевидное равенство
, влияющий на амплитуду дифрагированной волны, следовательно, на контраст. Удобно фазовый множитель представить в иной форме. Учитывая очевидное равенство 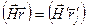 , где
, где  -векторы ОР и решетки не искаженного кристалла, а
-векторы ОР и решетки не искаженного кристалла, а  -локальный вектор ОР и вектор решетки искаженного кристалла, причем
-локальный вектор ОР и вектор решетки искаженного кристалла, причем  . Заменив
. Заменив  , получим
, получим  . Следовательно,
. Следовательно,  . При использованных выше допущениях векторы
. При использованных выше допущениях векторы  и
и 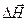 зависят только от z . Очевидно, что
зависят только от z . Очевидно, что 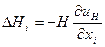 , где
, где  - компоненты вектора
- компоненты вектора 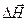 вдоль осей Х,Y,Z
вдоль осей Х,Y,Z  , а
, а  -проекция вектора
-проекция вектора  на
на  . Отсюда
. Отсюда  , и так как при дифракции быстрых электронов
, и так как при дифракции быстрых электронов  практически перпендикулярен оси Z, то локальный поворот отражающих плоскостей
практически перпендикулярен оси Z, то локальный поворот отражающих плоскостей  . Изменение межплоскостных расстояний определяет изменение
. Изменение межплоскостных расстояний определяет изменение  (ось Х направлена вдоль H). Проекция этой компоненты на s равна
(ось Х направлена вдоль H). Проекция этой компоненты на s равна  . Теперь окончательно в искаженной решетке локальный параметр
. Теперь окончательно в искаженной решетке локальный параметр  равен:
равен:
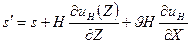 (6)
(6)
Существенным выводом из уравнения (5), необходимым для идентификации дефектов, является условие:
 (7)
(7)
При выполнении этого от условия контраста, вызванного полем смещения дефекта, нет, так как в колонках, искаженных им, амплитуда не отличается от амплитуды совершенного кристалла. Из (6) очевидно, что из-за малых значений брегговских углов 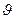 локальные изменения межплоскостных расстояний влияют на величину дополнительного фазового множителя
локальные изменения межплоскостных расстояний влияют на величину дополнительного фазового множителя  , а, следовательно, и на контраст гораздо слабее, чем локальные повороты решетки вокруг оси, перпендикулярной лучевой плоскости.
, а, следовательно, и на контраст гораздо слабее, чем локальные повороты решетки вокруг оси, перпендикулярной лучевой плоскости.
В общем случае дефекты характеризуются сильно анизотропными полями смещений, Знание поля смещений позволяет предсказать возможный контраст, связанный с тем или иным типом дефектов, и наоборот, по характеру контраста можно идентифицировать тип наблюдаемых дефектов. На этом и построено электронно-микроскопическое изучение дефектов кристаллов на основе дифракционного контраста.
Дислокации. Основные особенности контраста при изображении дислокаций удобно рассмотреть на примере винтовой дислокации, параллельной плоскости фольги. Пусть вектор Бюргерса  направлен вдоль оси Y (рис.11).Тогда поле смещений вокруг дислокации задается уравнением
направлен вдоль оси Y (рис.11).Тогда поле смещений вокруг дислокации задается уравнением 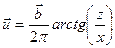 , x –расстояние от оси дислокации (направление осей показано на рис.11).Тогда для колонки, расположенной на расстоянии x от оси дислокации, дополнительный фазовый множитель
, x –расстояние от оси дислокации (направление осей показано на рис.11).Тогда для колонки, расположенной на расстоянии x от оси дислокации, дополнительный фазовый множитель
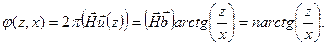
При n=0 очевидно , что контраста нет, то есть дислокация невидима. Условие  означает, что вектор
означает, что вектор  параллелен отражающим плоскостям и смещения
параллелен отражающим плоскостям и смещения 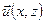 так же им параллельны.
так же им параллельны.
На рис.12 хорошо видно исчезновение части дислокаций, для которых выполняется условие  при формирующем изображение рефлексе 311, которые видны при использовании рефлекса 202.
при формирующем изображение рефлексе 311, которые видны при использовании рефлекса 202.
Поле смещений винтовой дислокации характеризуется отсутствием смещений , приводящих к изменению межплоскостных расстояний. Поэтому в уравнении (6) локальный параметр отклонения  содержит лишь два слагаемых
содержит лишь два слагаемых

Очевидно, что по разные стороны от оси дислокации при заданном  в зависимости от знака второго слагаемого величина
в зависимости от знака второго слагаемого величина  может по абсолютной величине уменьшаться или возрастать .Соответственно поле смещений в зависимости от знака n и х так разворачивает решетку кристалла, что она или удаляется или приближается к брегговскому положению по мере движения в колонке к z =0. Очевидно, при z>>x кривизна амплитудно-фазовой диаграммы определяется первым слагаемым, как это видно из рисунка ( рис.13)
может по абсолютной величине уменьшаться или возрастать .Соответственно поле смещений в зависимости от знака n и х так разворачивает решетку кристалла, что она или удаляется или приближается к брегговскому положению по мере движения в колонке к z =0. Очевидно, при z>>x кривизна амплитудно-фазовой диаграммы определяется первым слагаемым, как это видно из рисунка ( рис.13)
Очевидно, что при s >0 в колонке, расположенной на расстоянии х1>0 от оси дислокации 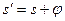 , а в колонке х2<0 ,
, а в колонке х2<0 , 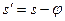 . Соответственно и амплитуды дифрагированного луча для колонок , где х2=const вдоль оси дислокации больше чем с противоположной стороны.
. Соответственно и амплитуды дифрагированного луча для колонок , где х2=const вдоль оси дислокации больше чем с противоположной стороны.
Очевидно, что изображение дислокации там, где амплитудно-фазовая диаграмма имеет вид развернутой спирали (рис.13).Очевидно, что светлопольное и темнопольное изображения дислокаций. Очевидно при пересечении линией дислокации экстинкционного контура (s=0), по обе стороны от которого параметр s имеет разные знаки, изображение дислокации располагается по разные стороны от оси дислокации. Изображение же дислокаций с противоположными направлениями вектора Бюргерса, смещены в противоположные стороны от их осей и при изменении знака s при покачивании к кристалла изображении дислокаций смещаются в противоположные стороны. Величина  должна быть достаточно большой, чтобы различие амплитуд искаженной и не искаженной колонок было не менее ~10% и контраст был заметен. Например, условие для обнаружения дислокаций
должна быть достаточно большой, чтобы различие амплитуд искаженной и не искаженной колонок было не менее ~10% и контраст был заметен. Например, условие для обнаружения дислокаций  . С ростом величины
. С ростом величины  контраст обычно усиливается. При больших значениях (например
контраст обычно усиливается. При больших значениях (например 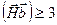 ) профиль изображения кроме основного может иметь и слабый побочный максимум (изображение как бы раздваивается). Обычно, ширина изображения близка по величине по величине его смещению от оси дислокации (рис.14) и составляет величину порядка 10-20 нм. Радиус амплитудно-фазовой диаграммы, а, следовательно, и величина амплитуды пропорциональна s-1. Поэтому дислокации лучше всего видны вблизи главных экстинкционных контуров (s
) профиль изображения кроме основного может иметь и слабый побочный максимум (изображение как бы раздваивается). Обычно, ширина изображения близка по величине по величине его смещению от оси дислокации (рис.14) и составляет величину порядка 10-20 нм. Радиус амплитудно-фазовой диаграммы, а, следовательно, и величина амплитуды пропорциональна s-1. Поэтому дислокации лучше всего видны вблизи главных экстинкционных контуров (s  ). В этом случае максимальна и ширина их изображений, хотя для количественных оценок контраста кинематические представления неприменимы и необходимо использовать динамическую теорию. Винтовая дислокация, расположенная наклонно к плоскости фольги имеет характерный осциллирующий контраст (рис.15). Причем в сравнительно толстых фольгах осцилляции сохраняются для наклонных участков лишь вблизи поверхности фольги. Для объяснения этого эффекта лучше использовать представления динамической теории. Осцилляции интенсивности на изображениях могут возникать благодаря тому, что дислокация располагается в области биения двух блоховских волн ( поля №1 и №2), интерференция которых и приводит к осцилляциям. Период осцилляций определяется экстинкционной длиной. Вблизи середины сравнительно толстой фольги, остается одна слабо поглощающаяся волна и осцилляции не видны.
). В этом случае максимальна и ширина их изображений, хотя для количественных оценок контраста кинематические представления неприменимы и необходимо использовать динамическую теорию. Винтовая дислокация, расположенная наклонно к плоскости фольги имеет характерный осциллирующий контраст (рис.15). Причем в сравнительно толстых фольгах осцилляции сохраняются для наклонных участков лишь вблизи поверхности фольги. Для объяснения этого эффекта лучше использовать представления динамической теории. Осцилляции интенсивности на изображениях могут возникать благодаря тому, что дислокация располагается в области биения двух блоховских волн ( поля №1 и №2), интерференция которых и приводит к осцилляциям. Период осцилляций определяется экстинкционной длиной. Вблизи середины сравнительно толстой фольги, остается одна слабо поглощающаяся волна и осцилляции не видны.
При рассмотрении контраста от дислокаций произвольного типа, поле смещений которой задано формулой :
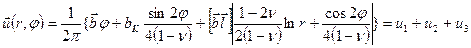 ,
,
(где 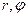 -полярные координаты,
-полярные координаты, 
 -вектор Бюргерса и его краевая компонента, пропорциональная
-вектор Бюргерса и его краевая компонента, пропорциональная 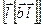 (
(  -единичный вектор, задающий направление оси дислокации),
-единичный вектор, задающий направление оси дислокации),  -компонента поля смещения, перпендикулярная плоскости скольжения), следует учесть, что на контраст влияют проекции всех трех компонент поля смещений на плоскость, параллельную вектору дифракции и перпендикулярную первичному пучку. Ясно, что изображение дислокации не «гаснет» даже если
-компонента поля смещения, перпендикулярная плоскости скольжения), следует учесть, что на контраст влияют проекции всех трех компонент поля смещений на плоскость, параллельную вектору дифракции и перпендикулярную первичному пучку. Ясно, что изображение дислокации не «гаснет» даже если  . Вектор Бюргерса определяют ,обычно. путем нахождения рефлекса, в котором изображение дислокации полностью или в существенной мере «гаснет». Не полное «гашение» изображения вызвано, при выполнении условия (Hb) =0 составляющим поля смещений u2 и u3. Если дислокация лежит в плоскости скольжения, нормальной первичному пучку, то только компоненты u1 и u2 влияют на контраст .В этом случае дополнительный фазовый сдвиг
. Вектор Бюргерса определяют ,обычно. путем нахождения рефлекса, в котором изображение дислокации полностью или в существенной мере «гаснет». Не полное «гашение» изображения вызвано, при выполнении условия (Hb) =0 составляющим поля смещений u2 и u3. Если дислокация лежит в плоскости скольжения, нормальной первичному пучку, то только компоненты u1 и u2 влияют на контраст .В этом случае дополнительный фазовый сдвиг
 .
.
В частности, для краевой дислокации 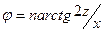 и изображение примерно вдвое шире , аналогично расположенной винтовой дислокации.
и изображение примерно вдвое шире , аналогично расположенной винтовой дислокации.
В принципе, если для краевой дислокации  , то контраст может быть обусловлен компонентой u3 . В этом случае дополнительный фазовый сдвиг не зависит от знака х и поэтому положение изображения симметрично относительно линии дислокации Так, если призматическая дислокационная петля образуется при ассоциации точечных дефектов в плоскости,
, то контраст может быть обусловлен компонентой u3 . В этом случае дополнительный фазовый сдвиг не зависит от знака х и поэтому положение изображения симметрично относительно линии дислокации Так, если призматическая дислокационная петля образуется при ассоциации точечных дефектов в плоскости,  параллельной плоскости фольги, то для нее выполняется условие
параллельной плоскости фольги, то для нее выполняется условие  и контраст вызван только компонентой u3. Радиус петли в этом случае равен радиусу ее изображения и может быть использован для оценки количества точечных дефектов, образовавших петлю. Однако, поскольку вдоль линии петли
и контраст вызван только компонентой u3. Радиус петли в этом случае равен радиусу ее изображения и может быть использован для оценки количества точечных дефектов, образовавших петлю. Однако, поскольку вдоль линии петли 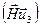 меняется, а там где
меняется, а там где  контраст уменьшается до нуля (рис.16). Для частичных дислокаций произведение
контраст уменьшается до нуля (рис.16). Для частичных дислокаций произведение  может быть и не целым числом. Так в кристалах с гранецентрированной кубической решеткой имеются дислокации Шокли с вектором Бюргерса типа
может быть и не целым числом. Так в кристалах с гранецентрированной кубической решеткой имеются дислокации Шокли с вектором Бюргерса типа  и Франка с
и Франка с  .В этом случае величина
.В этом случае величина 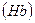 может иметь значения
может иметь значения  , где n=0 , 1 ,2 …. Расчеты показали, что при
, где n=0 , 1 ,2 …. Расчеты показали, что при  не видны как винтовые, так и краевые дислокации ( если компонента u3 не существенна). В случае
не видны как винтовые, так и краевые дислокации ( если компонента u3 не существенна). В случае  при малых отклонениях от условий Брега ( sLэ
при малых отклонениях от условий Брега ( sLэ 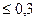 ) и дислокации Шокли и дислокации Франка видны, но при sLэ
) и дислокации Шокли и дислокации Франка видны, но при sLэ  , если (Hb)=-2/3, изображение дислокаций исчезает.
, если (Hb)=-2/3, изображение дислокаций исчезает.
Выше было сказано, что дислокации лучше всего выявляются при не слишком больших отклонениях от условий Брега. Но при этом и ширина их изображений достаточно велика, что и определяет разрешение метода ПЭМ при изучении дислокационного строения кристаллов с большой плотностью дислокаций. Увеличить разрешение метода и тем самым опираться на существенно более высокое разрешение самого микроскопа можно используя так называемый метод слабых пучков. В таких задачах как определение положения дислокаций при выявлении расщепления дислокаций для изучения механизма упрочнения и энергии дефектов упаковки, выявление дисперсных выделений в упругом поле дислокаций, изучение парных дислокаций в сверхструктурах или дислокационных диполей т.д. необходимо иметь меньшую ширину изображения и соответственно меньшие смещения изображений от истинного положения линий дислокаций. Метод слабых пучков может быть реализован в микроскопах с высоким разрешением темнопольных изображений, получаемых при больших значениях вектора s, например , 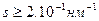 (при (Hb)<2) или sLэ>5.
(при (Hb)<2) или sLэ>5.
| <== предыдущая страница | | | следующая страница ==> |
| В компьютерной графике применяются три цветовые модели: RGB, CMYK и HSB | | | ВОДОХОЗЯЙСТВЕННЫЙ БАЛАНС |
Дата добавления: 2014-07-30; просмотров: 518; Нарушение авторских прав

Мы поможем в написании ваших работ!