
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Временной ряд без структурных и сезонных колебаний
Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренд. Этот способ называют аналитическим выравниванием временного ряда.
Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Чаще всего применяются следующие функции:
– линейный тренд;
– гипербола;
– экспоненциальный тренд;
– тренд в форме степенной функции;
– парабола второго и более высоких порядков.
Параметры каждого тренда можно определить обычным МНК, используя в качестве независимой переменной время, а в качестве зависимой переменной – фактические уровни временного ряда. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
Известно несколько способов определения типа тенденции; к наиболее распространенным относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровня ряда от времени, расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни yt и yt–1 тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчету по каждому уравнению скорректированного коэффициента детерминации 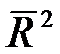 и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных.
и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных.
Пример. Имеются помесячные данные о номинальной заработной плате младшего медицинского персонала за 10 месяцев 1999 г. (табл.1). Требуется выбрать наилучший тип тренда и определить его параметры.
Таблица 1. Номинальная заработная плата младшего медицинского персонала за 10 месяцев 1999г., $
| Месяц | Номинальная месячная заработная плата |
| Январь | 82,9 |
| Февраль | 87,3 |
| Март | 99,4 |
| Апрель | 104,8 |
| Май | 107,2 |
| Июнь | 121,6 |
| Июль | 118,6 |
| Август | 114,1 |
| Сентябрь | 123,0 |
| Октябрь | 127,3 |
График данного временного ряда представлен на рис.1.
Из рис.1 видно наличие возрастающей тенденции, возможно существование линейного тренда.
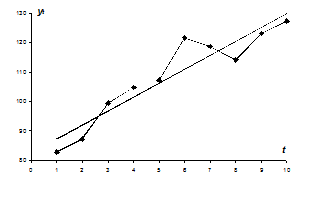
Рис.1. Динамика номинальной заработной платы младшего медицинского персонала за 10 месяцев 1999 г.
Для дальнейшего анализа определим коэффициенты автокорреляции по уровням этого ряда и их логарифмам (табл.2).
Таблица 2. Автокорреляционная функция временного ряда
| Лаг | Автокорреляционная функция | |
| по уровням ряда | по логарифмам уровней ряда | |
| 0,901 | 0,914 | |
| 0,805 | 0,832 | |
| 0,885 | 0,896 |
Высокие значения коэффициентов автокорреляции первого, второго и третьего порядков свидетельствуют о том, что ряд содержит тенденцию. Приблизительно равные значения коэффициентов автокорреляции по уровням ряда и по логарифмам уровней позволяют сделать следующий вывод: если ряд содержит нелинейную тенденцию, то она выражена в неявной форме. Поэтому для моделирования его тенденции в равной мере целесообразно использовать и линейную, и нелинейную функцию, например, степенной или экспоненциальный ряд.
Для выявления наилучшего уравнения тренда определим параметры основных видов трендов. Результаты этих расчетов представлены в табл.3, согласно данным которой, наилучшей является степенная форма тренда, для которой значение скорректированного коэффициента детерминации наиболее высокое. Это уравнение выглядит следующим образом:
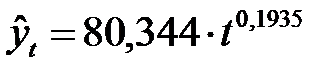
Таблица 3. Уравнения трендов для временного ряда
| Тип тренда | Уравнение | R2 |
| Линейный | yt = 82,66 + 4,72 × t | 0,887 |
| Парабола | yt = 72,9 + 9,6 × t – 0,444 × t2 | 0,937 |
| Степенной | yt = 80,344 × x0,1935 | 0,939 |
| Экспоненциальный | yt = 83,956 × e0,0451x | 0,872 |
| Гиперболический | yt = 4,43 – 47,63/t | 0,758 |
| Логарифмический | yt = 78,575 + 19,891 × ln(x) | 0,924 |
Наиболее простую экономическую интерпретацию имеют параметры линейного и экспоненциального трендов.
Параметры линейного тренда можно интерпретировать так: a – начальный уровень временного ряда в момент времени t = 0; b – средний за период абсолютный прирост уровней ряда. Применительно к данному временному ряду можно сказать, что номинальная месячная заработная платы младшего медицинского персонала за 10 месяцев изменялись от уровня 82,66$ со средним за месяц абсолютным приростом, равным 4,72$.
Расчетные значения уровней временного ряда по линейному тренду определяются двумя способами. Во-первых, можно последовательно подставлять в найденное уравнение тренда значения t = 1, 2, …, т.е.
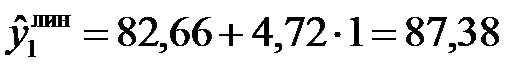 ;
;
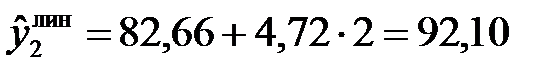 и т.д.
и т.д.
Во-вторых, в соответствии с интерпретацией параметров линейного тренда каждый последующий уровень ряда – это сумма предыдущего уровня и среднего цепного абсолютного прироста, т.е.
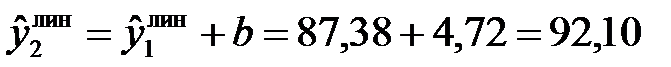 .
.
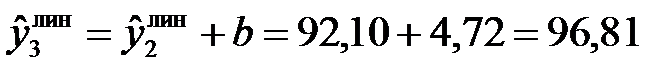 и т.д.
и т.д.
График линейного тренда приведен на рис.1.
Параметры экспоненциального тренда имеют следующую интерпретацию. Параметр a – это начальный уровень временного ряда в момент времени t = 0. Величина eb – это средний за единицу времени коэффициент роста уровней ряда.
Для нашего примера уравнение экспоненциального тренда имеет вид:
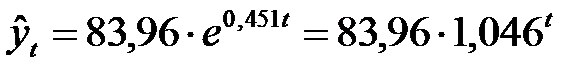
Таким образом, начальный уровень ряда в соответствии с уравнением экспоненциального тренда составляет 83,96% (сравните с начальным уровнем 82,66% в линейном тренде), а средний цепной коэффициент роста – 1,046. Следовательно, можно сказать, что номинальная месячная заработная плата изменялась от уровня 83,96$ со средним за месяц цепным ростом, равным104,6%. Иными словами, средний за месяц цепной темп прироста заработной платы составил 4,6%.
По аналогии с линейной моделью расчетные значения уровней ряда по экспоненциальному тренду можно получить как путем подстановки в уравнение тренда значений t = 1, 2, …, n, так и в соответствии с интерпретацией параметров экспоненциального тренда: каждый последующий его уровень – это произведение предыдущего уровня на соответствующий коэффициент роста:
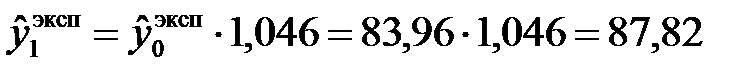 .
.
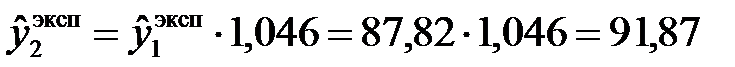 и т.д.
и т.д.
При наличии неявной нелинейной тенденции следует дополнять описанные выше методы выбора наилучшего уравнения тренда качественным анализом динамики изучаемого показателя, с тем чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблемы возможного наличия в исследуемом временном ряде поворотных точек и изменения темпов прироста, или ускорения темпов прироста, начиная с определенного момента (периода) времени под влиянием ряда факторов и т.д. В случае, если уравнение тренда выбрано неверно при больших значениях t, результаты анализа и прогнозирования динамики временного ряда с использованием выбранного уравнения будут недостоверными вследствие ошибки спецификации.
Если наилучшей формой тренда является парабола второго порядка, в то время как на самом деле имеет место линейная тенденция, то при больших значениях t парабола и линейная функция будут по разному описывать тенденцию в уровнях ряда. При t > t* парабола второго порядка характеризует убывающую тенденцию в уровнях ряда yt, а линейная функция – возрастающую (рис.2).
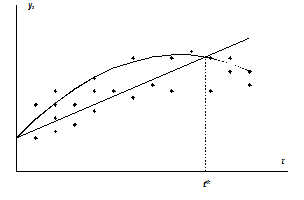
Рис.2. Ошибка спецификации при выборе уравнения тренда
| <== предыдущая страница | | | следующая страница ==> |
| Лекция . Моделирование тенденции временного ряда | | |
Дата добавления: 2014-08-04; просмотров: 702; Нарушение авторских прав

Мы поможем в написании ваших работ!