
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Физиология как наука. Предмет, задачи, методы, история физиологии
Стандартный (прямой) симплекс – метод производит направленный перебор допустимых базисных решений исходной задачи, при котором возрастает значение целевой функции.
Двойственный симплекс – метод также направлен на решение исходной задачи, но использует для этого допустимые базисные решения двойственной задачи.В процессе их перебора уменьшается значение целевой функции двойственной задачи 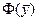 . процесс завершается при достижении
. процесс завершается при достижении 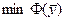 , что однозначно соответствует
, что однозначно соответствует 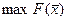 .
.
Принципиальным отличиемдвойственного симплекс – метода от стандартного (прямого) является то, что на любой итерации кроме последнейбазисное решение исходной задачи может быть недопустимым,т. к. базисные переменные не удовлетворяют условиям неотрицательности.
Рассмотрим следующий пример.
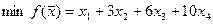 переход к
переход к 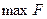 , где
, где 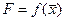
Определить 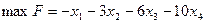
при ограничениях:
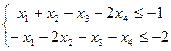
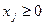 (
( 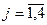 )
)
Соответствующая двойственная задача имеет вид:
Найти 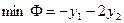
при ограничениях:
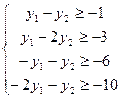
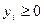 (
( 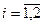 )
)
Перепишем ограничения обеих задач в виде неравенств.
Для этого введем слабые переменные  ,
,  и
и 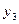 ,
, 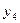 ,
, 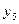 ,
, 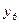 которые являются неотрицательными.
которые являются неотрицательными.
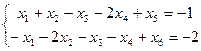
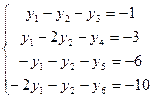
Составим расширенную симплекс – таблицу исходной задачи:
| Номер итерации | F, 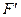 и базовая переменная и базовая переменная
| Значения |
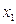
|

|

|
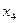
|

|

|
| F | ||||||||

| -1 | -1 | -2 | |||||

| -2 | -1 | -2 | -1 | -1 |
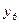
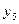
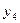
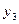 (
( 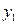 ) (
) ( 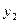 )
)
Выбранное базисное решение является недопустимым, т. к.  =-1 и
=-1 и  =-2, т. е. отрицательным.
=-2, т. е. отрицательным.
Однако все коэффициенты в строке F являются положительными. Поэтому выбранному недопустимому базисному решению исходной задачи соответствует допустимое базисное решение двойственной задачи.
Установим соответствие между переменными исходной и двойственной задач:
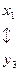
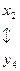
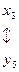
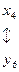
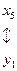
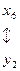
Для допустимого базисного решения двойственной задачи значения переменных:
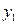 =0;
=0; 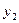 =0;
=0; 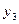 =1;
=1; 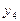 =3;
=3; 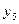 =6;
=6; 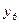 =10.
=10.
Суть двойственного симплекс – метода заключается в том, что на каждой итерации алгоритма определяется новое допустимое базисное решение двойственной задачи, при котором значение целевой функции 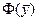 уменьшается.
уменьшается.
Для исходной задачи базисные переменные  и
и  являются недопустимыми. Поэтому необходимо одну из них вывести из базисных в свободные.Выбор такой переменной производится по наибольшей абсолютной величине из числа отрицательных базисных переменных. Соответствующая строка называется ведущей.
являются недопустимыми. Поэтому необходимо одну из них вывести из базисных в свободные.Выбор такой переменной производится по наибольшей абсолютной величине из числа отрицательных базисных переменных. Соответствующая строка называется ведущей.
Так как  =-1 и
=-1 и  =-2, то для перевода из базисных в свободные выбираем
=-2, то для перевода из базисных в свободные выбираем  .
.
Такой выбор можно обосновать, рассуждая относительно двойственной задачи,для которой  соответствует свободной переменной
соответствует свободной переменной 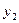 , которая имеет наибольший по абсолютной величине коэффициент в выражении для целевой функции
, которая имеет наибольший по абсолютной величине коэффициент в выражении для целевой функции 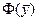 и, следовательно, должна быть переведена в базисные переменные.
и, следовательно, должна быть переведена в базисные переменные.
Для выбора свободной переменной исходной задачи, которая должна стать базисной,продолжается рассмотрение двойственной задачи.
При переводе 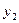 изсвободных в базисные ее значение будет увеличиваться от нуля в положительную сторону. Первая из базисных переменных
изсвободных в базисные ее значение будет увеличиваться от нуля в положительную сторону. Первая из базисных переменных 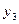 ,
, 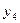 ,
, 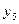 ,
, 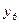 , которая при этом станет равной нулю, должна быть переведена в свободные. Выразим эти переменные из ограничений:
, которая при этом станет равной нулю, должна быть переведена в свободные. Выразим эти переменные из ограничений:
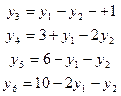
Учитывая, что 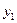 =0 (свободная переменная), получим значения
=0 (свободная переменная), получим значения 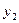 ,при которых соответствующие переменные
,при которых соответствующие переменные 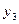 ,
, 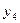 ,
, 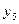 ,
, 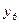 станут равными нулю.
станут равными нулю.
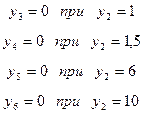
Следовательно, для перевода из базисных переменных в свободные для двойственной задачи нужно выбрать переменную 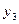 .
.
Возвращаясь к исходной задаче, заключаем, что для перевода из свободных в базисныевыбираем переменную  , которая соответствует
, которая соответствует 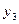 .
.
Сформулируем соответствующее правило выбора для симплекс – таблицы исходной задачи.
Для выбора свободной переменной, переводимой в базисные, вычисляются отрицательные отношения элементов 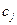 строки F к элементам
строки F к элементам 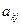 строки
строки 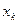 , где
, где 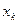 - переменная, переводимая из базисных в свободные на текущей итерации. При этом не рассматриваются неотрицательные отношения,для которых знаменатель
- переменная, переводимая из базисных в свободные на текущей итерации. При этом не рассматриваются неотрицательные отношения,для которых знаменатель 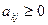 . В итоге выбирается переменная, которая соответствует наибольшему значению отношения (более близкому к нулю).
. В итоге выбирается переменная, которая соответствует наибольшему значению отношения (более близкому к нулю).
В нашем примере это переменная  (см таблицу).
(см таблицу).
Замечание:Если все коэффициенты строки 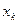 являются неотрицательными, т. е.
являются неотрицательными, т. е. 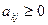 для всех j, то оптимальное решение не существует, т. к. целевая функция
для всех j, то оптимальное решение не существует, т. к. целевая функция 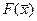 исходной задачи не ограничена сверху (или целевая функция
исходной задачи не ограничена сверху (или целевая функция 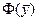 двойственной задачи не ограничена снизу).
двойственной задачи не ограничена снизу).
После выбора необходимых переменных производится смена базиса (как и в прямом симплекс – методе) и переход к следующей итерации.
Таким образом,в двойственном симплекс – методе, в отличии от прямого, сначала определяется переменная, которая должна быть выведена из базисных, а затем – переменная, переводимая из свободных в базисные. При этом используется симплекс – таблица такой же формы, что и в прямом методе. Однако двойственный симплекс – метод начинает работу с допустимогобазисного решения двойственной задачи и сохраняет его допустимым на всех итерациях.
Продолжая решение примера получим:
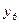
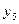
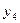
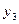 (
( 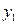 ) (
) ( 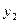 )
)
| Номер итерации | F, 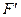 и базовая переменная и базовая переменная
| Значения |
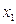
|

|

|
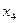
|

|

|
| F | ||||||||

| -1 | -1 | -2 | |||||

| -2 | -1 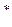
| -2 | -1 | -1 | |||
| F | -2 | |||||||

| -3 | -1 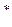
| -2 | -3 | ||||
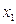
| -1 | |||||||
| F | -5 | |||||||

| -1 | -1 | ||||||
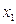
| -4 | -3 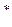
| -5 | |||||
| F | -9 | |||||||

| 
| 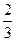
| - 
| 
| - 
| |||

| 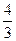
| - 
| 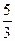
| - 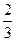
| - 
|
В результате получено оптимальное решение исходной задачи:
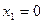 ;
; 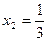 ;
; 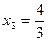 ;
; 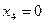 ;
; 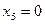 ;
; 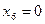 , для которого F=-9.
, для которого F=-9.
Оптимальное значение целевой функции двойственной задачи  =-9 при базисном решении:
=-9 при базисном решении:
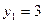 ;
; 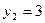 ;
; 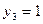 ;
; 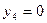 ;
; 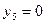 ;
; 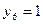 .
.
В заключение следует отметить,что двойственный симплекс – метод применяется для решения тех задач, для которых не удается использовать прямой симплекс – метод.
Например:
1) при решении задачи 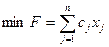 , где
, где 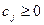 (
( 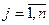 ). Здесь можно получить эквивалентную
). Здесь можно получить эквивалентную 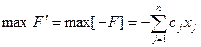
2) при наличии ограничений вида 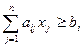 (
(  ), где ограничения преобразуются к исходному виду
), где ограничения преобразуются к исходному виду 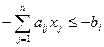 (
(  ) и свободные члены становятся отрицательными.
) и свободные члены становятся отрицательными.
кроме того возможны комбинации указанных случаев, а также задачи, в которых для полученного оптимального решения в систему ограничений вводятся дополнительные условия, делающие это решение недопустимым. Тогда, чтобы не выполнять расчеты снова, используется двойственный симплекс – метод.
Подобные случаи возникают очень часто при решении задач целочисленного ЛП.
В том случае, когда и должно быть решение, отсутствует как для исходной, так и для двойственной задачи, т. е. среди элементов 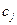 и
и 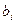 имеются отрицательные, решение задачи включает два этапа:
имеются отрицательные, решение задачи включает два этапа:
1) С помощью двойственного симплекс – метода исключаются все отрицательные базисные переменные 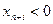 (или
(или 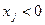 );
);
2) С использованием стандартногосимплекс – метода находится оптимальное решение задачи.
На первом этапе при использовании двойственного симплекс – метода изменяется правило выбора ведущего столбца:
Среди отрицательных коэффициентов 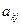 ведущей строки выбрать элемент
ведущей строки выбрать элемент 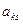 , для которого отношение
, для которого отношение
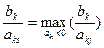
Пример:
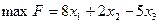
при ограничениях:
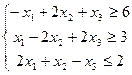
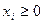 (
( 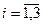 )
)
Переходим к канонической форме ограничений:
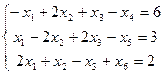
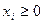 (
( 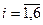 )
)
Умножаем на (-1) первое и второе уравнения:
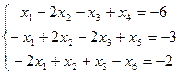
Симплекс – таблица имеет вид:
| Номер итерации | F, 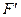 и базовая переменная и базовая переменная
| Значения |
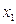
|

|

|
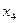
|

|

|
| F | -8 | -2 | ||||||
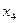
| -6 | -2 | -1 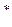
| |||||

| -3 | -1 | -2 | |||||

| -1 | |||||||
| F | -30 | -3 | -12 | |||||

| -1 | -1 | ||||||

| -3 | 6 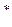
| -2 | |||||

| ||||||||
| F | -12 | -9 | ||||||

| - 
| - 
| ||||||

| 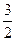
| 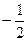
| - 
| 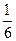
| ||||

| 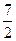
| 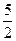 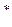
| 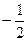
| |||||
| F | 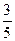
| 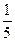
| 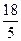
| |||||

| - 
| - 
| ||||||

| 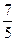
| - 
| 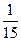
| 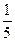
| ||||
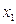
| 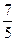
| - 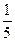
| 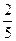
|
Замечание: отношения 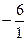 и
и 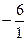 ;
; 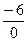 не рассматриваются, т.к. знаменатель
не рассматриваются, т.к. знаменатель 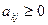
Оптимальное решение: 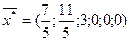
Физиология как наука. Предмет, задачи, методы, история физиологии
Физиология (физис - природа) - это наука о нормальных процессах жизнедеятельности организма, составляющих его физиологических систем, отдельных органов, тканей, клеток и субклеточных структур, механизмах регуляции этих процессов и влиянии на функции организма естественных факторов внешней среды.
Исходя из этого, в целом предметом физиологии является здоровый организм. Задачи физиологии включены в ее определение. Основным методом физиологии является эксперимент на животных. Выделено 2 основных разновидности экспериментов или опытов:
1.Острый опыт или вивисекция (живосечение). В процесс него производится хирургическое вмешательство, исследуются функции открытого или изолированного органа. После этого не добиваются выживания животного. Продолжительность острого эксперимента от нескольких десятков минут до нескольких часов (пример).
2.Хронический опыт. В процессе хронических опытов производят оперативное вмешательство для получения доступности к органу. Затем добиваются заживления операционных ран и лишь после этого приступают к исследованиям. Продолжительность хронических экспериментов может составлять многие годы (пример).
Иногда выделяют подострый эксперимент (пример).
Вместе с тем, для медицины требуются сведения о механизмах функционирования человеческого организма. Поэтому И.П. Павлов писал:” Экспериментальные данные, можно применять к человеку только с осторожностью, постоянно проверяя фактичность сходства с деятельностью этих органов у человека и животных". Следовательно, без постановки специальных наблюдений и опытов на человеке изучение его физиологии бессмысленно. Поэтому выделяют специальную физиологическую науку - физиологию человека, Физиология человека имеет предмет, задачи, методы и историю. Предметом физиологии человека является здоровый человеческий организм.
Её задачи:
1.Исследование механизмов функционирования клеток, тканей, органов, систем организма человека в целом
2. Изучение механизмов регуляции функций органов и систем организма.
3. Выявление реакций человеческого организма и его систем на изменение внешней и внутренней среды.
Так как физиология в целом экспериментальная наука, основным методом физиологии человека также является эксперимент. Однако эксперименты на человеке коренным образом отличаются от опытов на животных. Во-первых, подавляющее большинство исследований на человеке производится с помощью неинвазивных методов, т.е. без вмешательства в органы и ткани (пример ЭКГ, ЭЭГ, ЭМГ, анализы крови и т.д.). Во-вторых, эксперименты на человеке проводят только тогда, когда они не наносят вреда здоровью и с согласия испытуемого. Иногда острые опыты проводятся на человеке в клинике, когда этого требуют задачи диагностики (пример). Однако следует отметить, что без данных классической физиологии возникновение и развитие физиологии человека было бы невозможно (памятники лягушке и собаке). Еще И.П. Павлов, оценивая роль физиологии для медицины, писал: "Понимаемые в грубом смысле слова физиология и медицина не отделимы, знание физиологии необходимо врачу любой специальности". А также, что "Медицина лишь обогащаясь постоянно изо дня в день, новыми физиологическими фактами, станет, наконец тем, чем она должна быть в идеале, т.е. умением чинить испортившийся механизм человека и быть прикладным знанием физиологии" (примеры из клиники). Другой известнейший русский физиолог проф. В.Я. Данилевский отмечал: "Чем точнее и полнее будут определены признаки нормы для телесной и душевной жизни человека, тем правильнее будет диагноз врача для ее патологических отклонений”.
Физиология, являясь основополагающей биологической наукой, тесно связана с другими фундаментальными и биологическими науками. В частности, без знания законов физики невозможно объяснение биоэлектрических явлений, механизмов свето- и звуковосприятия. Без применения данных химии невозможно описание процессов обмена веществ, пищеварения, дыхания и т.д., Поэтому на границах этих наук с физиологией выделились дочерние науки биофизика и биохимия.
Так как структура и функция неразделимы, причем именно функция определяет формирование структуры, физиология тесно связана с морфологическими науками: цитологией, гистологией, анатомией.
В результате исследования действия различных химических веществ на организм из физиологии выделилась в самостоятельные науки фармакология и токсикология. Накопление данных о нарушениях механизмов функционирования организма при различных заболеваниях послужило основой возникновения патологической физиологии.
Выделяют общую и частную физиологию. Общая физиология изучает основные закономерности жизнедеятельности организма, механизмы таких базисных процессов как обмен веществ и энергии, размножение, процессы возбуждения и т.д. Частная физиология исследует функции конкретных клеток, тканей, органов и физиологических систем. Поэтому в ней выделяются такие разделы, как физиология мышечной ткани, сердца, почек, пищеварения, дыхания и т.д. Кроме того, в физиологии выделяют разделы имеющие специфический предмет исследования или особые подходы в исследовании функций. К ним относятся эволюционная физиология (объяснение), сравнительная физиология, возрастная физиология.
В физиологии имеется целый ряд прикладных разделов. Это, например, физиология сельскохозяйственных животных. В физиологии человека выделяют следующие прикладные разделы:
1.Возрастня физиология. Изучает возрастные особенности функций организма.
2.Физиология труда.
3.Клиническая физиология. Это наука, использующая физиологические методики и подходы для диагностики и анализа патологических отклонений.
4.Авиационная и космическая физиология.
5.Физиология спорта.
Физиология человека теснейшим образом связана с такими клиническими дисциплинами, как терапия, хирургия, акушерство, эндокринология, психиатрия, офтальмология и т.д. Например, эти науки используют для диагностики многочисленные методики разработанные физиологами. Отклонения нормальных параметров организма являются основой выявления патологии.
Некоторые разделы физиологии человека являются базой для психологии. Это физиология центральной нервной системы, высшей нервной деятельности, сенсорных систем, психофизиология.
История физиологии подробно описана в учебнике под ред. Ткаченко
| <== предыдущая страница | | | следующая страница ==> |
| Двойственный симплекс – метод | | | МЕХАНИЗМЫ РЕГУЛЯЦИИ ФУНКЦИЙ ОРГАНИЗМА |
Дата добавления: 2014-08-04; просмотров: 402; Нарушение авторских прав

Мы поможем в написании ваших работ!