
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Двойственный симплекс – метод
|
Читайте также: |
Стандартный (прямой) симплекс – метод производит направленный перебор допустимых базисных решений исходной задачи, при котором возрастает значение целевой функции.
Двойственный симплекс – метод также направлен на решение исходной задачи, но использует для этого допустимые базисные решения двойственной задачи.В процессе их перебора уменьшается значение целевой функции двойственной задачи 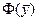 . процесс завершается при достижении
. процесс завершается при достижении 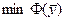 , что однозначно соответствует
, что однозначно соответствует 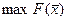 .
.
Принципиальным отличиемдвойственного симплекс – метода от стандартного (прямого) является то, что на любой итерации кроме последнейбазисное решение исходной задачи может быть недопустимым,т. к. базисные переменные не удовлетворяют условиям неотрицательности.
Рассмотрим следующий пример.
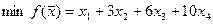 переход к
переход к 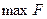 , где
, где 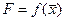
Определить 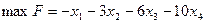
при ограничениях:
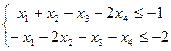
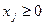 (
( 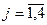 )
)
Соответствующая двойственная задача имеет вид:
Найти 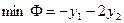
при ограничениях:
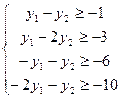
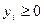 (
( 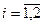 )
)
Перепишем ограничения обеих задач в виде неравенств.
Для этого введем слабые переменные  ,
,  и
и 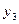 ,
, 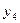 ,
,  ,
,  которые являются неотрицательными.
которые являются неотрицательными.
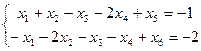
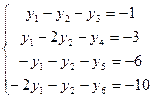
Составим расширенную симплекс – таблицу исходной задачи:
| Номер итерации | F, 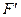 и базовая переменная и базовая переменная
| Значения |
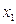
|

|

|
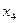
|

|

|
| F | ||||||||

| -1 | -1 | -2 | |||||

| -2 | -1 | -2 | -1 | -1 |
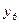
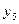
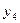
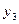 (
( 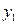 ) (
) ( 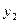 )
)
Выбранное базисное решение является недопустимым, т. к.  =-1 и
=-1 и  =-2, т. е. отрицательным.
=-2, т. е. отрицательным.
Однако все коэффициенты в строке F являются положительными. Поэтому выбранному недопустимому базисному решению исходной задачи соответствует допустимое базисное решение двойственной задачи.
Установим соответствие между переменными исходной и двойственной задач:
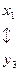
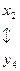
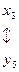
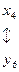
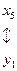
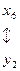
Для допустимого базисного решения двойственной задачи значения переменных:
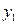 =0;
=0; 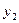 =0;
=0; 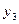 =1;
=1; 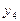 =3;
=3; 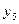 =6;
=6; 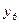 =10.
=10.
Суть двойственного симплекс – метода заключается в том, что на каждой итерации алгоритма определяется новое допустимое базисное решение двойственной задачи, при котором значение целевой функции 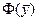 уменьшается.
уменьшается.
Для исходной задачи базисные переменные  и
и  являются недопустимыми. Поэтому необходимо одну из них вывести из базисных в свободные.Выбор такой переменной производится по наибольшей абсолютной величине из числа отрицательных базисных переменных. Соответствующая строка называется ведущей.
являются недопустимыми. Поэтому необходимо одну из них вывести из базисных в свободные.Выбор такой переменной производится по наибольшей абсолютной величине из числа отрицательных базисных переменных. Соответствующая строка называется ведущей.
Так как  =-1 и
=-1 и  =-2, то для перевода из базисных в свободные выбираем
=-2, то для перевода из базисных в свободные выбираем  .
.
Такой выбор можно обосновать, рассуждая относительно двойственной задачи,для которой  соответствует свободной переменной
соответствует свободной переменной 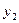 , которая имеет наибольший по абсолютной величине коэффициент в выражении для целевой функции
, которая имеет наибольший по абсолютной величине коэффициент в выражении для целевой функции 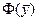 и, следовательно, должна быть переведена в базисные переменные.
и, следовательно, должна быть переведена в базисные переменные.
Для выбора свободной переменной исходной задачи, которая должна стать базисной,продолжается рассмотрение двойственной задачи.
При переводе 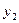 изсвободных в базисные ее значение будет увеличиваться от нуля в положительную сторону. Первая из базисных переменных
изсвободных в базисные ее значение будет увеличиваться от нуля в положительную сторону. Первая из базисных переменных 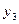 ,
, 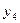 ,
, 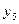 ,
, 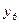 , которая при этом станет равной нулю, должна быть переведена в свободные. Выразим эти переменные из ограничений:
, которая при этом станет равной нулю, должна быть переведена в свободные. Выразим эти переменные из ограничений:
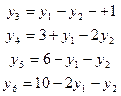
Учитывая, что 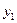 =0 (свободная переменная), получим значения
=0 (свободная переменная), получим значения 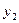 ,при которых соответствующие переменные
,при которых соответствующие переменные 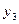 ,
, 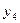 ,
, 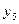 ,
, 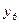 станут равными нулю.
станут равными нулю.
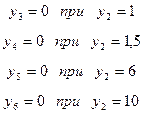
Следовательно, для перевода из базисных переменных в свободные для двойственной задачи нужно выбрать переменную 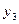 .
.
Возвращаясь к исходной задаче, заключаем, что для перевода из свободных в базисныевыбираем переменную  , которая соответствует
, которая соответствует 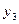 .
.
Сформулируем соответствующее правило выбора для симплекс – таблицы исходной задачи.
Для выбора свободной переменной, переводимой в базисные, вычисляются отрицательные отношения элементов 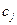 строки F к элементам
строки F к элементам 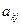 строки
строки 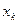 , где
, где 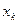 - переменная, переводимая из базисных в свободные на текущей итерации. При этом не рассматриваются неотрицательные отношения,для которых знаменатель
- переменная, переводимая из базисных в свободные на текущей итерации. При этом не рассматриваются неотрицательные отношения,для которых знаменатель 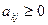 . В итоге выбирается переменная, которая соответствует наибольшему значению отношения (более близкому к нулю).
. В итоге выбирается переменная, которая соответствует наибольшему значению отношения (более близкому к нулю).
В нашем примере это переменная  (см таблицу).
(см таблицу).
Замечание:Если все коэффициенты строки 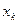 являются неотрицательными, т. е.
являются неотрицательными, т. е. 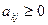 для всех j, то оптимальное решение не существует, т. к. целевая функция
для всех j, то оптимальное решение не существует, т. к. целевая функция 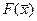 исходной задачи не ограничена сверху (или целевая функция
исходной задачи не ограничена сверху (или целевая функция 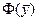 двойственной задачи не ограничена снизу).
двойственной задачи не ограничена снизу).
После выбора необходимых переменных производится смена базиса (как и в прямом симплекс – методе) и переход к следующей итерации.
Таким образом,в двойственном симплекс – методе, в отличии от прямого, сначала определяется переменная, которая должна быть выведена из базисных, а затем – переменная, переводимая из свободных в базисные. При этом используется симплекс – таблица такой же формы, что и в прямом методе. Однако двойственный симплекс – метод начинает работу с допустимогобазисного решения двойственной задачи и сохраняет его допустимым на всех итерациях.
Продолжая решение примера получим:
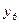
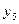
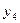
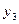 (
( 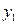 ) (
) ( 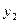 )
)
| Номер итерации | F, 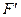 и базовая переменная и базовая переменная
| Значения |
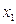
|

|

|
|

|

|
| F | ||||||||

| -1 | -1 | -2 | |||||

| -2 | -1 
| -2 | -1 | -1 | |||
| F | -2 | |||||||

| -3 | -1 
| -2 | -3 | ||||
| -1 | |||||||
| F | -5 | |||||||

| -1 | -1 | ||||||
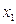
| -4 | -3 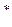
| -5 | |||||
| F | -9 | |||||||

| 
| 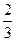
| - 
| 
| - 
| |||

| 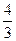
| - 
| 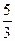
| - 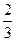
| - 
|
В результате получено оптимальное решение исходной задачи:
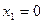 ;
; 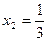 ;
; 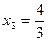 ;
; 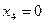 ;
; 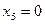 ;
; 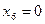 , для которого F=-9.
, для которого F=-9.
Оптимальное значение целевой функции двойственной задачи 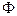 =-9 при базисном решении:
=-9 при базисном решении:
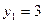 ;
; 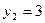 ;
; 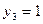 ;
; 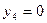 ;
; 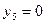 ;
; 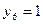 .
.
В заключение следует отметить,что двойственный симплекс – метод применяется для решения тех задач, для которых не удается использовать прямой симплекс – метод.
Например:
1) при решении задачи 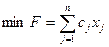 , где
, где 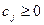 (
( 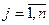 ). Здесь можно получить эквивалентную
). Здесь можно получить эквивалентную 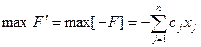
2) при наличии ограничений вида 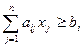 (
(  ), где ограничения преобразуются к исходному виду
), где ограничения преобразуются к исходному виду 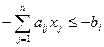 (
(  ) и свободные члены становятся отрицательными.
) и свободные члены становятся отрицательными.
кроме того возможны комбинации указанных случаев, а также задачи, в которых для полученного оптимального решения в систему ограничений вводятся дополнительные условия, делающие это решение недопустимым. Тогда, чтобы не выполнять расчеты снова, используется двойственный симплекс – метод.
Подобные случаи возникают очень часто при решении задач целочисленного ЛП.
В том случае, когда и должно быть решение, отсутствует как для исходной, так и для двойственной задачи, т. е. среди элементов 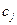 и
и 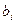 имеются отрицательные, решение задачи включает два этапа:
имеются отрицательные, решение задачи включает два этапа:
1) С помощью двойственного симплекс – метода исключаются все отрицательные базисные переменные 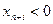 (или
(или 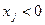 );
);
2) С использованием стандартногосимплекс – метода находится оптимальное решение задачи.
На первом этапе при использовании двойственного симплекс – метода изменяется правило выбора ведущего столбца:
Среди отрицательных коэффициентов 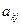 ведущей строки выбрать элемент
ведущей строки выбрать элемент 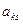 , для которого отношение
, для которого отношение
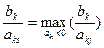
Пример:
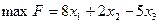
при ограничениях:
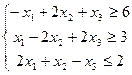
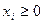 (
( 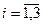 )
)
Переходим к канонической форме ограничений:
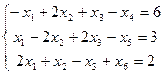
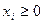 (
( 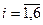 )
)
Умножаем на (-1) первое и второе уравнения:
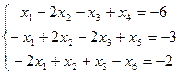
Симплекс – таблица имеет вид:
| Номер итерации | F, 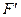 и базовая переменная и базовая переменная
| Значения |
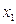
|

|

|
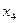
|

|

|
| F | -8 | -2 | ||||||
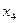
| -6 | -2 | -1 
| |||||

| -3 | -1 | -2 | |||||

| -1 | |||||||
| F | -30 | -3 | -12 | |||||

| -1 | -1 | ||||||

| -3 | 6 
| -2 | |||||

| ||||||||
| F | -12 | -9 | ||||||

| - 
| - 
| ||||||

| 
| 
| - 
| 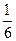
| ||||

| 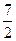
| 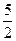 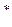
| 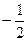
| |||||
| F | 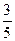
| 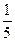
| 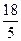
| |||||

| - 
| - 
| ||||||

| 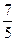
| - 
| 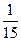
| 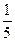
| ||||
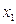
| 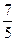
| - 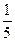
| 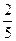
|
Замечание: отношения 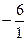 и
и 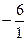 ;
; 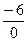 не рассматриваются, т.к. знаменатель
не рассматриваются, т.к. знаменатель 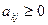
Оптимальное решение: 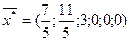
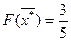
| <== предыдущая страница | | | следующая страница ==> |
| Табличная форма двойственной пары задач ЛП | | | Физиология как наука. Предмет, задачи, методы, история физиологии |
Дата добавления: 2014-08-04; просмотров: 723; Нарушение авторских прав

Мы поможем в написании ваших работ!