Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Табличная форма двойственной пары задач ЛП
Для одновременного представления прямой и двойственной задач также используется табличная форма записи.
Введем слабые переменные в обе задачи двойственной пары:
( 
);
( 
)
( )
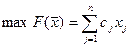
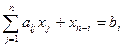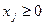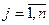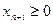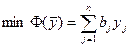
при ограничениях:
( );
( )
( )
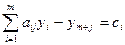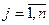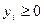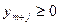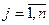Выберем в каждой задаче слабые переменные в качестве базисных, получим табличную форму для каждой из задач, а также совмещенную таблицу.
-1 
… 
- 
| - 
| … | - 
| |
| 
| 
| … | 
|
| 
| 
| … | 
|
| … | … | … | … | … |
| 
| 
| … | 
|
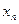
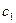
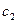
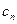
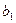
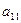
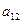
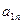
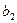
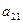
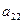
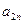
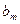
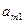
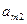
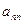
=-F
= 
= 
= 
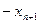
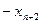
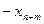
Для исходной задачи каждому уравнению соответствует строка таблицы (подобно табличному симплекс – методу). Чтобы получить исходную формулировку каждый коэффициент в строке умножают на соответствующую переменную над таблицей. Затем полученные произведения складываются, и результат будет равен переменной справа от таблицы.
Двойственная задача определяется столбцами данной таблицы и формируется следующим образом:
| -
| -
| … | -
| |
|
|
|
| … |
|
|
|
|
| … |
|
| … | … | … | … | … |
|
|
|
| … |
|
= 
= 
… = 
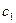
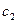
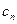
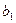
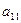
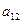
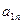
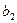
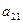
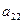
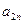
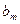
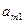
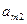
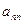
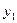
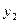
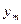
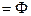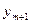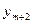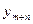
Таким образом, прямая и двойственная задачи могут быть описаны единой таблицей, в которой установлено следующее соответствие переменных:
-1 …
| -
| -
| … | -
| |
|
|
|
| … |
|
|
|
|
| … |
|
| … | … | … | … | … |
|
|
|
| … |
|
= = … =
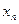
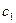
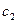
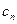
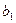
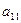
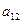
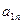
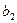
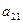
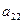
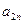
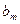
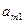
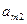
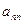
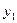
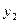
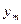
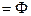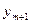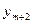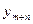
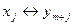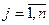( ) и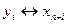 
( )
Таблица такого вида называется сокращенной симплекс – таблицей, т. к. в ней отсутствуют столбцы (строки), соответствующие базисным переменным.
Рассмотрим особенноститакой симплекс – таблицы.
1) Любое преобразование таблицы, соответствующее смене базиса исходной задачи,дает новую таблицу, которая описывает как исходную,так и двойственнуюзадачи.
2) Элементы первой строки, соответствующие коэффициентам при свободных переменных в выражении для целевой функции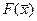 
исходной задачи, всегда совпадают со значениями базисных переменныхдвойственной задачи.
3) Элементы первого столбца, соответствующиебазисным переменным (свободным членам) исходной задачи, всегда совпадают с коэффициентами при свободных переменных в выражении для целевой функции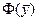 
двойственной задачи.
4) Если элементы первой строки и первого столбца неотрицательны(возможно, кроме элемента на их пересечении), то достигнуто оптимальное решение как исходной, так и двойственной задач.
Рассмотрим полученное утверждение.
Для исходной задачи неотрицательные элементы первого столбца говорят о том, что базисное решение является допустимым. Если при этом положительны коэффициенты первой строки, то достигнут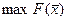 
- см описание симплекс – метода.
Для двойственной задачинеотрицательные элементы первой строки говорят о том, что базисное решение является допустимым. Положительные элементы первого столбца означают получение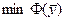 
. Минимизация 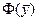обусловлена процедурой заполнения таблицы. Первая строка соответствует 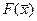, а первый столбец соответствует - .
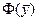Отсюда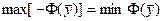 
.
| <== предыдущая страница | | | следующая страница ==> |
| Двойственная задача ЛП | | | Двойственный симплекс – метод |
Дата добавления: 2014-08-04; просмотров: 254; Нарушение авторских прав
Мы поможем в написании ваших работ!