
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Двойственная задача ЛП
|
Читайте также: |
Рассмотрим две следующие задачи:
Задача 1
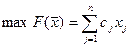
при ограничениях:
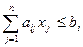 (
(  );
);
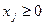 (
( 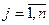 ).
).
Задача 2
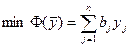
при ограничениях:
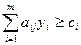 (
( 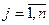 );
);
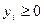 (
(  ).
).
Эти задачи образуют так называемую двойственную парузадач ЛП. Первая задача называется исходной, а вторая – двойственной.
В этих задачах используются одни и те же константы, однако исходная задача является задачей максимизации, а двойственная – задачей минимизации. Число переменных двойственной задачи равно числу ограничений исходной и наоборот; знаки неравенств в ограничениях являются обратными; коэффициенты целевой функции одной задачи являются свободными членами ограничений другой.
Пример записи двойственной задачи:
Исходная задача
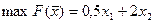
при ограничениях
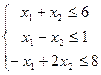
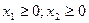
Двойственная задача
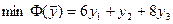
при ограничениях
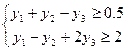
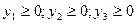
Между решениями исходной и двойственной задач существует точная связь, которую можно представить следующими свойствами:
1) Любое допустимое решение исходной задачиопределяет оценку снизудля оптимального значения целевой функции двойственной задачи;
2) Любое допустимое решение двойственной задачидает оценку сверхудля целевой функции исходной задачи;
3) Для оптимальных решений прямой и двойственной задач значения целевых функций совпадают.
Если 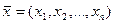 и
и 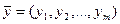 - допустимые решения прямой и двойственной задач соответственно, то первые два свойства означают, что всегда выполняется неравенство
- допустимые решения прямой и двойственной задач соответственно, то первые два свойства означают, что всегда выполняется неравенство
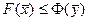
Для оптимальных решений 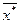 и
и 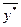 справедливо выражение
справедливо выражение
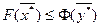
Чтобы доказать эти положения: 1) умножимкаждое i – е ограничение прямой задачи на 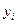 , наоборот, каждое j – е ограничение двойственной задачи на
, наоборот, каждое j – е ограничение двойственной задачи на 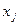 .
.
Так как 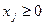 (
( 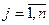 ) и
) и 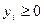 (
(  ), то знаки не изменяются:
), то знаки не изменяются:
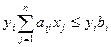 (
(  );
);
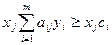 (
( 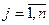 );
);
Суммируем все соотношения в каждой группе:
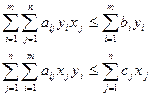
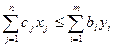 или
или 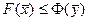 .
.
Для доказательства полученного положения отметим, что неравенство 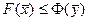 выполняется также и для оптимального решения двойственной задачи
выполняется также и для оптимального решения двойственной задачи 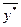 , т. е.
, т. е.
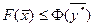
При этом, как следует из постановки прямой задачи справедливо неравенство
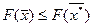
Отсюда получаем, что 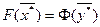 .
.
Аналогичные рассуждения можно привести и для оптимального решения исходной задачи 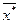 , для которого
, для которого
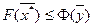
Одновременно имеем, что 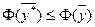 . Отсюда также получаем, что
. Отсюда также получаем, что 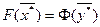 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Метод искусственного базиса | | | Табличная форма двойственной пары задач ЛП |
Дата добавления: 2014-08-04; просмотров: 448; Нарушение авторских прав

Мы поможем в написании ваших работ!