
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Глава II. Транспортная задача
В предыдущих разделах мы рассматривали симплекс-метод решения задачи линейного программирования. Однако для ряда задач матрица, используемая в симплекс-методе, имеет специальный вид. Поэтому для таких задач разработаны специальные методы решения, позволяющие быстрее найти решение. В этой главе мы разберем одну из таких задач - транспортную задачу.
2.1. Замкнутая модель транспортной задачи.
Пусть в пунктах A1,…,Am производится некоторый продукт в количествах a1,…,am > 0. Этот продукт перевозится в пункты B1,…,Bn, где он полностью потребляется в количествах b1,…,bn > 0. Для каждой пары индексов i,j задана стоимость cij  0 перевозок единицы продукта из пункта производства Ai в пункт потребления Bj. Необходимо перевезти весь произведенный продукт из пунктов A1,…,Am в пункты потребления B1,…,Bn. При этом требуется, чтобы потребности каждого из пунктов B1,…,Bn полностью удовлетворялись.
0 перевозок единицы продукта из пункта производства Ai в пункт потребления Bj. Необходимо перевезти весь произведенный продукт из пунктов A1,…,Am в пункты потребления B1,…,Bn. При этом требуется, чтобы потребности каждого из пунктов B1,…,Bn полностью удовлетворялись.
Сформулируем эту задачу как задачу линейного программирования.
Назовем планом перевозок неотрицательную матрицу X = (xij) размера m×n, в которой число xij ≥ 0 указывает количество продукта, перевозимого из пункта Ai в пункт Bj, 1 ≤ i ≤ m, 1 ≤ j ≤ n.
Стоимость z(X) перевозок является линейной функцией от X, именно, z(X) = ∑i,j cijxij, xij ≥ 0.
В задаче требуется найти такой план перевозок X, чтобы его стоимость была бы минимальной, причем весь продукт был бы вывезен из пунктов производства, доставлен в пункты потребления, и все потребности были бы полностью удовлетворены. Отсюда следует, что транспортная задача является задачей линейного программирования. Действительно то, что весь продукт, производимый в Ai вывозится записывается в виде уравнения
∑j xij = ai , ( i = 1, …, m )
Аналогично, условие того, что потребности пункта Bj полностью удовлетворены, записывается в виде уравнения
∑i xij = bj, ( j = 1, …, n ).
Таким образом, транспортная задача следующим образом записывается как задача линейного программирования
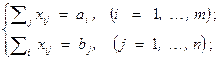 (1)
(1)
xij ≥ 0;
z(X) = ∑i,j cijxij → min.
Сформулированная в (1) транспортная задача называется замкнутой моделью.
Другие модели транспортной задачи будут рассмотрены позднее.
Назовем план перевозок X допустимым, если выполнены все ограничения из (1). Укажем способ построения допустимого решения методом минимального элемента.
Этот способ возможен, если ∑i ai = ∑j bj. Для этого выберем клетку с индексами (i,j), в которой стоит минимальное из чисел cij. В эту клетку помещаем число xij = min(ai ,bj ). Если ai < bj, то все остальные элементы i-ой строки полагаем равными нулю, число bj заменяем на bj – ai, а ai на 0. Если же ai ≥ bj, то все остальные элементы j-ого столбца полагаем равными нулю, число ai заменяем на ai – bj, а bj на 0. В результате число пустых строк или столбцов уменьшается на единицу. Продолжая этот процесс, получаем первоначальный план.
Продемонстрируем этот метод на конкретном примере. Пусть a1 = 18, a2 = 10, a3 = 12, b1 = 16, b2 = 9, b3 = 15, а матрица C имеет вид
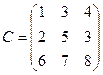
Построим вспомогательную таблицу
| b1 = 16 | b2 = 9 | b3 = 15 | ||||
| a1 = 18 | с11=1 | с12=3 | с13=4 | |||
| a3 = 10 | с21=2 | с22=5 | с23=3 | |||
| a3 = 12 | c31=6 | c32=7 | c33=5 | |||
Минимальный элемент с11=1. В клетку (1,1) помещаем min(18,16)=16. В соответствии с изложенным правилом получаем таблицу
| b1 = 0 | b2 = 9 | b3 = 15 | ||||
| a1 = 2 | с11=1 | с12=3 | с13=4 | |||
| a3 = 10 | с21=2 | с22=5 | с23=3 | |||
| a3 = 12 | c31=6 | c32=7 | c33=5 | |||
Далее из всех незаполненных клеток, находящихся в двух последних столбцах выбираем ту, в которой число cij минимально. Это, например, с23=3. Применяя общее правило, получаем новую таблицу
| b1 = 0 | b2 = 9 | b3 = 5 | ||||
| a1 = 2 | с11=1 | с12=3 | с13=4 | |||
| a3 = 0 | с21=2 | с22=5 | с23=3 | |||
| a3 = 12 | c31=6 | c32=7 | c33=5 | |||
Далее выбираем клетку (1,2) с с12=3. Получаем новую таблицу
| b1 = 0 | b2 = 7 | b3 = 5 | ||||
| A1 = 0 | с11=1 | с12=3 | с13=4 | |||
| A3 = 0 | с21=2 | с22=5 | с23=3 | |||
| A3 = 12 | c31=6 | c32=7 | c33=5 | |||
Наконец завершаем процесс и получаем первоначальный план. При этом можно отбросить первую строку и первый столбец. Получаем
| с11=1 | с12=3 | с13=4 | |||
| с21=2 | с22=5 | с23=3 | |||
| c31=6 | c32=7 | c33=5 | |||
Теорема 1. Транспортная задача (1) имеет решение тогда и только тогда, когда
∑i ai = ∑j bj.
Доказательство. Пусть решение X существует. Тогда из (1) вытекает, что
∑i ai = ∑i ∑j xij = ∑j ∑i xij = ∑j bj.
Обратно, пусть выполнено равенство из условия теоремы. Тогда можно построить хотя бы одно допустимое решение, например, методом минимального элемента.
Из ограничений видно, что все элементы допустимой матрицы неотрицательны и потому ограничены. Следовательно, функция z(X) достигает минимума на некотором допустимом плане, т.е. транспортная задача всегда имеет решение.
Рассмотрим двойственную задачу линейного программирования к транспортной задаче (1). В соответствии с общим правилом запишем (1) в виде
∑j xij ≤ ai , i = 1, …, m;
- ∑j xij ≤ - ai , i = 1, …, m;
∑i xij ≤ bj, j = 1, …, n; (2)
- ∑i xij ≤ - bj, j = 1, …, n
xij ≥ 0;
- z(X) = - ∑i,j cijxij → max.
Тогда двойственная задача имеет вид
ai’ - ai’’ + βj’ - βj’’ ≥ - cij , i = 1, …, m, j = 1, …, n;
ai’,ai’’,βj’, βj’’ ≥ 0, i = 1, …, m, j = 1, …, n; (3)
T’= a1’a1 – a1’’a1 + … + am’am – am’’am + β1’b1 – β1’’b1 + … + βm’bm – βm’’bm → min
Положим T = -T’ и ai = ai’’ - ai’, βj = βj’’ - βj’, i = 1, …, m, j = 1, …, n.
Тогда (3) имеет вид
ai + βj ≤ cij , i = 1, …, m, j = 1, …, n; (4)
T = a1a1 + … + amam + β1b1 + … + βmbm → max.
Теорема 2. Для того, чтобы допустимый план перевозок X был оптимальным необходимо и достаточно, чтобы существовали такие числа (потенциалы) a1, … , am,β1, … , βn, для которых
1) ai + βj ≤ cij при всех i,j;
2) ai + βj = cij, если xij > 0.
Доказательство. Проверим достаточность. Пусть задан допустимый план X = (xij), и a1, … , am,β1, … , βn из условий теоремы. Предположим, что Y = (yij) - произвольный допустимый план. В силу ограничений (1) и свойств 1), 2) из условия теоремы получаем
z(Y) = ∑i,j cijyij ≥ ∑i,j (ai + βj)yij = ∑i ai ∑j yij + ∑j βj ∑i yij = ∑i ai ai + ∑j βj bj = ∑i ai ∑j xij + ∑j βj ∑i xij = ∑i,j (ai + βj)xij = ∑i,j cijxij = z(X).
Проверим теперь необходимость. Пусть X 0= (xij0) – оптимальный план и a1, … , am,β1, … , βn – оптимальное решение двойственной задачи. По (4) выполнено неравенство 1) из условия теоремы. Кроме того, по теореме о равновесии получаем (ai+ βj - cij) xij0 = 0. Поэтому если xij0 > 0, то выполнено равенство 2) из условия теоремы.
Перейдем к изложению алгоритма решения транспортной задачи при некоторых ограничениях. Транспортная задача называется вырожденной, если существуют такие подмножества индексов
G Í {1, … ,m }, H Í {1, … ,n},
что одно из них собственное и
åi Î G ai = åj Î H bj
Другими словами, суммарный запас продукта в пунктах Ai, i Î G, совпадает с потреблением в пунктах Bj, j Î H.
Далее мы будет предполагать, что рассматриваемая транспортная задача невырождена. Изложим метод потенциалов решения невырожденной транспортной задачи, опирающийся на теорему 2. Мы уже имеем допустимый первоначальный план, построенный методом минимального элемента. Из этого построения видно, что число ненулевых элементов в первоначальном плане равно n + m – 1. Найдем первоначальную систему потенциалов. Для этого в соответствии с условием 2) из теоремы 2 составим систему из n + m – 1 линейного уравнения
ai + βj = cij.
В этой системе число неизвестных ai,βj равно n + m. Можно показать, что ранг этой матрицы равен n + m – 1. Поэтому одно из неизвестных является свободным. Полагаем его равным нулю и далее находим частное решение системы. Продемонстрируем этот шаг на рассмотренном выше примере. Имеем системы линейных уравнений

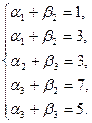
Положим a1 = 0. Тогда β1 = 1, β2 = 3. Далее a3 = 4, β3 = 1, a2 = 2.
Для полученной системы потенциалов проверяем выполняется ли условие 1) из теоремы 2. Для этого составляем вспомогательную матрицу D, в которой на месте (i,j) стоит dij = ai + βj . Если dij £ cij для всех (i,j), то построенный план по теореме 2 является оптимальным. Далее вычисляем значение целевой функции z(X) для этого плана. В нашем примере
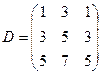
Мы видим, что условие 1) нарушается в клетке (1,2).
Опишем основной шаг алгоритма, состоящий в улучшении плана. Выберем клетку (p,q), в которой ap + βq > cpq. По построению xpq = 0. Нам потребуется
Предложение. Пусть план X = (xij) допустим, и xpq = 0 для некоторой пары индексов (p,q). Тогда существует и единственная такая последовательность различных строк p = i(0), i(1), … , i(k) и различных столбцов j(1), … , j(k-1), j(k) = q в матрице X, что элементы этой матрицы, стоящие в клетках (i(0), j(1)), (i(1), j(1)), (i(1), j(2)), (i(2), j(2)), … , (i(k), j(k-1)), (i(k), j(k)), отличны от нуля.
Заметим, что если мы начнем движение по матрице X с клетки (p,q), двигаясь далее по клеткам (i(0), j(1)), (i(1), j(1)), (i(1), j(2)), (i(2), j(2)), … , (i(k), j(k-1)), (i(k), j(k)) из предложения, то мы сначала идем по строке, далее по столбцу, затем снова по строке и т. д. На последнем шаге мы идем по строке и попадаем в исходный столбец с номером q.
Расставим во всех выбранных клетках чередующиеся метки +, - , начиная с + в начальной выбранной клетке (p,q). Пусть q - минимальный среди элементов xij, стоящих в выбранных клетках с меткой -. В клетках с меткой + число xij увеличиваем на q, а в клетках с меткой - уменьшаем на q. Все остальные элементы матрицы X не меняем. Получаем новый допустимый план X’ = (xij’). Сравним значения целевых функций для планов X и X’. Имеем
z(X') - z(X) = åi,j cij(x'ij - xij) = ås=0k-1 ci(s)j(s)(x'i(s)j(s) - xi(s)j(s) ) +
ås=0k ci(s)j(s+1)(x'i(s)j(s+1) - xi(s)j(s+1) ) = ås=0k-1 ci(s)j(s)q - ås=0k ci(s)j(s+1)q = q[ ci(0)j(0) + (ai(1) + bj(1)) + ¼ + (ai(k-1) + bj(k-1)) - (ai(0) + bj(1)) - … - (ai(k-1) + bj(k))] = q[ ci(0)j(0) - (ai(0 + bj(k))] < 0.
Итак, план улучшился. Для нового плана снова находим систему потенциалов и с помощью теоремы 2 проверяем его оптимальность и т. д. В результате через конечное число шагов в результате работы этого алгоритма получаем оптимальный план.
Продемонстрируем работу этого алгоритма на рассмотренному выше примере. Мы выбрали клетку (2,1). Выбираем путь (2,3), (3,4), (3,2), (1,2), (1,1). Расставляем метки + для клеток (2,1), (3,4), (1,2), и метки – для клеток (2,3), (3,2), (1,1). Минимальный элемент q стоящий в клетках с меткой – равен 7. Изменяем матрицу и получаем новую таблицу
| с11=1 | с12=3 | с13=4 | |||
| с21=2 | с22=5 | с23=3 | |||
| c31=6 | c32=7 | c33=5 | |||
Для новой таблицы пишем систему уравнений для нахождения потенциалов:
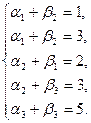
Полагаем a1 = 0. Тогда β1 = 1, и поэтому β2 = 3, a2 = 1. Далее β3 = 2, a3 = 3. Таким образом, матрица D имеет вид
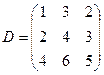
В соответствии с теоремой 2 построенный план
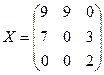
оптимален. Поэтому ответом является
z(X) = 9´1 + 9´3 + 7´2 + 3´3 + 12´5 = 9 + 27 + 14 + 9 + 60 =119.
2.2. Другие модели транспортной задачи.
1. Открытая модель. Пусть производится больше продукта, чем потребляется, т. е. ∑i ai > ∑j bj. Тогда вводится фиктивный пункт Bn+1, с потреблением bn+1= ∑i ai - ∑j bj, причем стоимость перевозки в него всегда равна 0. Тогда возникает замкнутая модель и ее решение будет оптимальным решением для исходной модели.
Аналогично, если ∑i ai < ∑j bj, то вводится фиктивный производитель An+1, с производством an+1= ∑j bj - ∑i ai, причем стоимость перевозки из него нулевая. Тогда снова возникает замкнутая модель и ее решение будет оптимальным решением для исходной модели.
2. Блокирование перевозок. Если по пути (i,j) перевозки запрещены, то полагаем, что cij = M – достаточно большое число, которое «не меняется при всех наших преобразованиях», т. е. при прибавлении к нему конечных чисел. Тогда перевозки по этому пути не могут быть осуществлены ввиду большой их стоимости.
3. Фиксированные перевозки. Пусть по пути (i,j) перевозки имеют фиксированное значение rij. В этом случае из ai и bj вычитается rij. Далее применяется модель с запретом перевозки по этому пути.
4. Дополнительные требования. Пусть по пути (i,j) перевозки должны иметь значение xij ³ rij. Тогда из ai и bj вычитается rij и далее решается обычная транспортная задача. Если же дано ограничение xij £ rij, то заявку bj заменяется на rij и вводится новый потребитель с потреблением bj - rij. Тарифы перевозок в новый пункт те же, что и в Bj, за исключением тарифа из Ai, который становится равным достаточно большому числу M.
Глава III. Игровые методы и модели.
3.1. Понятие об игровых моделях.
Необходимость использования математических моделей в коммерческой деятельности связана с количественным обоснованием решений. В зависимости от степени определенности возможных исходов, с которыми сталкивается лицо, принимающее решение, встречаются три типа моделей:
1) выбор решений в условиях определенности, когда относительно каждого действия известно к какому конкретному исходу оно приведет;
2) выбор решения в условиях риска, когда каждое действие приводит к одному из множества исходов, причем известна вероятность появления каждого исхода;
3) выбор решений в условиях неопределенности, когда действия стороны имеют своим следствием множество исходов, вероятности которых вообще неизвестны.
В экономике при решении практических задач приходится анализировать ситуации, где налицо две (или более) конкурирующие стороны, преследуют противоположные цели, причем результат каждой из сторон зависит от того, какой образ действий выбирает противоположная сторона.
В коммерческой деятельности часто возникают конфликтные ситуации, где в качестве противоположных сторон выступают торговые фирмы, промышленные предприятия, продавцы, покупатели и т.д.
Теория игр представляет собой математическую теорию конфликтных ситуаций. Ее задача заключается в выработке рекомендаций по рациональному поведению участников конфликта.
Каждая конфликтная ситуация в коммерческой деятельности сложна, и ее анализ затруднен наличием многих влияющих факторов. Чтобы сделать возможным проведение математического анализа ситуации, необходимо выделить существенные факторы и построить схематизированную модель, которую называют игрой. Стороны, участвующие в конфликтных ситуациях, называются игроками (отдельные лица или коллективы). Исход игры (конфликта) называется выигрышем или проигрышем.
Развитие игры во времени происходит последовательно, по этапам или ходам. Ходом в теории игр называют выбор одного из предусмотренных правилами игры действия. Они бывают личные и случайные. Личным ходом называют сознательный выбор игроком одного из возможных вариантов действия и его реализация. Случайным ходом называют выбор, осуществляемый не волевым решением игрока, а каким-либо механизмом случайного выбора (бросание монеты, пасовка, сдача карт и т.п.).
Одним из основных понятий теории игр является стратегия. Стратегий игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе этого игрока в зависимости от ситуации, сложившейся в процессе игры.
Оптимальной стратегией игрока называется такая стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш (или, что-то же самое, минимально возможный средний проигрыш). Выбор этой стратегии основан на предположении, что противная сторона по меньшей мере так же разумна, как и мы сами, и делает все для того, чтобы помешать нам добиться поставленной цели.
В большинстве конфликтных ситуаций при выборе разумной стратегии приходится принимать во внимание не один, а несколько показателей. Причем стратегия, оптимальная по одному показателю, необязательно будет оптимальной и по другим.
В зависимости от причин, вызывающих неопределенность исходов, игры можно разделить на следующие основные группы.
Комбинаторные игры. Комбинаторными называются игры, в которых правила дают, в принципе, возможность каждому игроку проанализировать все разнообразные варианты своего поведения и, сравнив эти варианты, выбрать тот из них, который ведет к наилучшему для этого игрока исходу. Неопределенность исхода связана обычно с тем, что количество возможных вариантов поведения (ходов) слишком велико и практически игрок не в состоянии их всех перебрать и проанализировать.
Азартные игры. Азартныминазываются игры, исход которых оказывается неопределенным в силу влияния различных случайных факторов. Азартные игры состоят только из случайных возможных ходов, при анализе которых применяется теория вероятностей.
Стратегические игры. Стратегическими называются игры, в которых неопределенность исхода вызвана тем, что каждый из игроков, принимая решение о выборе предстоящего хода, не знает, какой стратегии будут придерживаться другие участники игры, причем незнание игрока о поведении и намерениях партнеров носит принципиальный характер, так как отсутствует информация о последующих действиях противника (партнера).
Существуют игры, сочетающие в себе свойства комбинаторных и азартных игр, стратегичность игр может сочетаться с комбинаторностью и т.д.
В игре могут сталкиваться интересы двух или более игроков.
Если в игре участвуют два игрока — игра называется парной, если число игроков больше двух — множественной. Участники множественной игры могут образовывать коалиции (постоянные или временные). Множественная игра с двумя коалициями превращается в парную. Парные игры получили наибольшее распространение в практике анализа игровых ситуаций.
Различают игры также и по сумме выигрыша. Игра называется игрой с нулевой суммой, если один игрок выигрывает ровно столько, сколько проигрывает другой, т.е. сумма выигрыша и проигрыша сторон равна нулю. В парной игре с нулевой суммой интересы игроков прямо противоположны. Парная игра с нулевой суммой называется антагонистической игрой. Игры, в которых выигрыш одного игрока и проигрыш другого не равны между собой, называются играми с ненулевой суммой.
В зависимости от числа возможных стратегий игры делятся на конечные и бесконечные.
Игра называется конечной, если у каждого игрока имеется только конечное число стратегий. Игра называется бесконечной, если хотя бы у одного игрока имеется бесконечное число стратегий.
По количеству ходов, которые делают игроки для достижения своих целей, игры бывают одношаговые и многошаговые. Одношаговые игры заключаются в том, что игрок выбирает одну из доступных ему стратегий и делает всего один единственный ход. Многошаговые игры заключаются в том, что игроки для достижения своих целей делают последовательно ряд ходов, которые могут ограничиваться правилами игры, либо могут продолжаться до тех пор, пока у одного из игроков не останется ресурсов для продолжения игры.
В последнее время получили большое распространение так называемые деловые игры. Деловая игра имитирует взаимодействие людей в виде упражнения в цепочечке принятия решений, основанной на модели - содержания коммерческой деятельности и на исполнении участниками игры соответствующих должностей – долей.
Деловые игры предназначены для воспроизведения и согласования коммерческих интересов. В основе конструкции игры лежит взаимосвязь ресурсов и использование знаний об их возможностях. Деловые игры имитируют организационно-экономические взаимодействия в различных звеньях коммерческих организаций и предприятий. Элементами игровой модели являются: участники игры; правила игры; информационный массив, отражающий состояние и движение ресурсов моделируемой хозяйственной системы. Преимущества игровой имитации перед реальным объектом таковы: наглядность последствий принимаемых решений, переменный масштаб времени; повторение имеющегося опыта с изменением установок; переменный масштаб охвата торговых явлений и объектов. Основными направлениями использования деловых игр являются следующие — в учебном процессе, например, обучение моделированию; для торговых работников, проверке их компетентности; в научных исследованиях; в разработке планов коммерческой деятельности.
В деловых играх игрокам обычно задаются начальные условия, в которых они находятся, сообщаются правила проведения игры, представляются варианты возможных решений и оценка их последствий. В иге обязательно присутствует «ведущий», который руководит игрой, оценивает принятые игроками решения, состояния, в которых они могут находиться в процессе игры, и определяет выигрыши и проигрыши по исходам игры.
Основными вопросами теории игр, которые возникают в коммерческой деятельности, являются:
1. В чем состоит оптимальность поведения каждого из игроков в игре?
2. Существуют ли стратегии игроков, которые обладали бы атрибутами оптимальности?
3. Если существуют оптимальные стратегии, то как их найти?
На практике, если у игрока нет точного представления о том, что такое оптимум, то вопрос о его поисках оказывается беспредметным, и все усилия по его нахождению могут оказаться напрасной тратой времени.
3.2. Постановка игровых задач.
Формальное описание задачи принятия решения можно представить в виде математической модели, задав множество 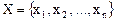 , элементы которого в теории игр называют альтернативами, множество
, элементы которого в теории игр называют альтернативами, множество 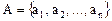 , элементы которого называются исходами и множество
, элементы которого называются исходами и множество 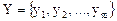 , элементы которого называются показателями среды, характеризующие условия коммерческой деятельности.
, элементы которого называются показателями среды, характеризующие условия коммерческой деятельности.
При анализе ситуаций, возникающих в коммерческой практике, множество X описывает набор принимаемых решений одной стороны, множество Y — возможные варианты поведения противоположной стороны, а множество A — тот выигрыш (или проигрыш), который получит игрок.
Если каждая альтернатива может привести к одному из исходов, каждый из которых имеет определенную вероятность появления, то считается, что принятие решения происходит в условиях риска.
Если каждая альтернатива может привести к одному из нескольких исходов, причем отсутствует даже стохастическая зависимость исходов от альтернатив, то считается, что принятие решения происходит в условиях неопределенности.
Каждый исход a Î A является функцией двух аргументов: 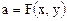 , где x Î X, y Î Y. Функция F называется функцией реализации и она сопоставляется исход по каждой паре - «альтернатива - состояние среды».
, где x Î X, y Î Y. Функция F называется функцией реализации и она сопоставляется исход по каждой паре - «альтернатива - состояние среды».
Функцию реализации удобно представить в виде так называемой платежной таблицы.
y1 ... yj ... ym
x1 F(x1, y1) ... F(x1, yj) ... F(x1, ym)
... ... ... ... ... ...
xi F(xi, y1) ... F(xi, yj) ... F(xi, ym)
... ... ... ... ... ...
xn F(xn, y1) ... F(xn, yj) ... F(xn, ym)
3.3. Методы и модели решения игровых задач.
Принцип минимакса.
Рассмотрим методы и модели решения игровых задач.
Рассмотрим конечную парную игру с нулевой суммой. Игрок I имеет m стратегий (А1, А2, ..., Аm), а игрок II — n стратегий (В1, В2, ..., Вn). Такая игра называется игрой размерностью m ´ n. Пусть каждая сторона определилась с выбором стратегии: игрок I — Ai (i = 1, 2, ..., m), игрок II — Bj (j = 1, 2, ..., n). Выигрыши игрока I — 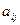 (Ai, Bj) и игрока II —
(Ai, Bj) и игрока II — 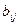 (Ai, Bj) удовлетворяют соотношению
(Ai, Bj) удовлетворяют соотношению 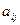 (Ai, Bj) +
(Ai, Bj) + 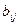 (Ai, Bj) = 0.
(Ai, Bj) = 0.
Если игра состоит только из личных ходов, то выбор стратегии (Ai, Bj) однозначно определяет исход игры 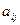 , т.е. выигрыш игрока I. Если игра содержит также случайные ходы, то выигрыш при паре стратегий (Ai, Bj) есть величина случайная, зависящая от исходов всех случайных ходов. В этом случае ожидаемый выигрыш — это среднее значение (математическое ожидание). Предположим, что значения aij известны для каждой пары стратегий (Ai, Bj). Построим таблицу, строки которой соответствуют стратегиям игрока I, а столбцы — стратегиям игрока II, т.е. платежную матрицу. Каждый элемент (aij > 0) матрицы определяет величину выигрыша игрока I и проигрыш игрока II. Цель игрока I — максимизировать свой выигрыш, а игрока II — минимизировать свой проигрыш. Платежная матрица имеет следующий вид:
, т.е. выигрыш игрока I. Если игра содержит также случайные ходы, то выигрыш при паре стратегий (Ai, Bj) есть величина случайная, зависящая от исходов всех случайных ходов. В этом случае ожидаемый выигрыш — это среднее значение (математическое ожидание). Предположим, что значения aij известны для каждой пары стратегий (Ai, Bj). Построим таблицу, строки которой соответствуют стратегиям игрока I, а столбцы — стратегиям игрока II, т.е. платежную матрицу. Каждый элемент (aij > 0) матрицы определяет величину выигрыша игрока I и проигрыш игрока II. Цель игрока I — максимизировать свой выигрыш, а игрока II — минимизировать свой проигрыш. Платежная матрица имеет следующий вид:
I \ II B1 B2 ... Bj ... Bn
A1 a11 a12 ... a1j ... a1n a1
A2 a21 a22 ... a2j ... a2n a2
... ... ... ... ... ... ... ...
Ai ai1 ai2 ... aij ... ain ai
... ... ... ... ... ... ... ...
Am am1 am2 ... amj ... amn am
Βj b1 b2 ... bj ... bn
Задача состоит в определении:
1) наилучшей (оптимальной) стратегии игрока I из стратегий A1, A2, ..., Am;
2) наилучшей (оптимальной) стратегии игрока II из стратегий B1, B2, ..., Bm.
Для решения задачи применяется принцип, согласно которому участники игры одинаково разумны и каждый из них делает все для того, чтобы добиться своей цели.
Проанализируем последовательно каждую стратегию игрока I. Если игрок I выбирает стратегию А1, то игрок II может выбрать такую стратегию Bj, при которой выигрыш игрока I будет равен наименьшему из чисел a1j:
 .
.
Выбирая стратегию Ai, игрок I должен рассчитывать на то, что в результате разумных действий игрока II он не выиграет больше, чем ai. Поэтому игрок I должен выбрать ту стратегию, для которой ai максимально:
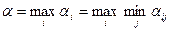 .
.
Величина a — гарантированный выигрыш, который может обеспечить себе игрок I при любом поведении игрока II. Величина a называется нижней ценой игры или максимином, а стратегия Аi игрока I, обеспечивающая получение нижней цены игры, называется максиминной чистой стратегией. При этом игрок I при любом поведении игрока II обеспечивает себе выигрыш, не меньше a: ai ³ a (i = 1, 2, ..., m).
Игрок II заинтересован в том, чтобы уменьшить свой проигрыш, т.е. обратить выигрыш игрока I в минимум. Для выбора оптимальной стратегии он должен найти максимальное значение выигрыша в каждом столбце:
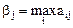 .
.
и среди этих значений выбрать наименьшее:  .
.
Величина b называется верхней ценой игры или минимаксом. Стратегия игрока II, обеспечивающая получение верхней цены игры, называется минимаксной чистой стратегией. Применяя ее, игрок II проиграет не больше b при любых действиях игрока I:
bj £ b (j = 1, 2, ..., n), причем всегда справедливо неравенство a £ b.
Таким образом, придерживаясь максиминной стратегии Ai, игрок I желает получить выигрыш не менее a не зависимо от действий игрока II, а игрок II, придерживаясь минимаксной стратегии Bj, гарантирует себе проигрыш не больше b.
Принцип, диктующий игрокам соответствующих стратегий (максиминной и минимаксной), в теории игр называется принципом минимакса. Этот принцип был впервые сформулирован Дж. фон Нейманом в 1928 году.
Пример 1. Дана платежная матрица. Найти решение игры: определить нижнюю и верхнюю цены игры и минимаксные стратегии:
I \ II B1 B2 B3 B4 a
A1 5 3 8 2 2
 A2 1 6 4 3 1
A2 1 6 4 3 1
 A3 9 5 4 7 4
A3 9 5 4 7 4
Βj 9 6 8 7
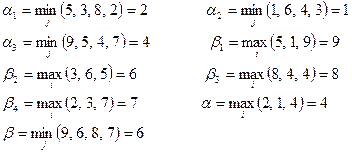
Таким образом, нижней цене игры (a = 4) соответствует стратегия A3 игрока I. Выбирая эту стратегию, игрок I достигнет выигрыша не меньше 4 при любом поведении игрока II. Верхней цене игры (b = 6) соответствует стратегия игрока II — В2. Эти стратегии являются минимаксными. Если обе стороны будут придерживаться этих стратегий, выигрыш будет равен а33 = 4.
Существуют матричные игры, для которых нижняя цена игры равна верхней, т.е. a = b. Такие игры называются играми с седловой точкой.
В этом случае g = a = b называется чистой ценой игры, а стратегии игроков 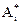 и
и 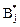 , позволяющие получить это значение — оптимальными. Пара
, позволяющие получить это значение — оптимальными. Пара 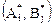 называется седловой точкой матрицы, так как элемент
называется седловой точкой матрицы, так как элемент 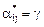 одновременно является минимальным в i-й строке и максимальным в j-м столбце. Оптимальные стратегии
одновременно является минимальным в i-й строке и максимальным в j-м столбце. Оптимальные стратегии 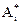 и
и 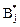 и чистая цена являются решением игры в чистых стратегиях, т.е. без привлечения механизма случайного выбора.
и чистая цена являются решением игры в чистых стратегиях, т.е. без привлечения механизма случайного выбора.
Пример 2. пусть задана платежная матрица. Найти нижнюю и верхнюю цены игры.
I II B1 B2 B3 a
A1 5 1 2 1
A2 2 6 2 2
A3 3 4 3 3
b 5 6 3
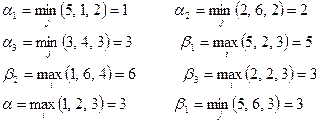
Следовательно a = b = g = 3.
Седловой точкой является пара альтернатив (А3, В3).
3.4. Решения игр в смешанных стратегиях.
Если матричная игра содержит седловую точку, то ее решение находится по принципу минимакса. Если же платежная матрица не имеет седловую точку, то применение минимаксных стратегий каждым из игроков показывает, что игрок I обеспечит себе выигрыш не меньше a, а игрок II обеспечит себе проигрыш не больше b. Так как a < b, то игрок I стремится увеличить выигрыш, а игрок II уменьшить проигрыш. Если информация о действиях противной стороны будет отсутствовать, то игроки будут многократно применять чистые стратегии случайным образом с определенной вероятностью. Такая стратегия в теории игр называется смешанной стратегией. Смешанная стратегия игрока — это полный набор его чистых стратегий при многократном повторении игры в одних и тех же условиях с заданными вероятностями. Для применения смешанных стратегий должны быть следующие условия:
1) в игре отсутствует седловая точка;
2) игроками используется случайная смесь чистых стратегий с соответствующими вероятностями;
3) игра многократно повторяется в одних и тех же условиях;
4) при каждом из ходов один игрок не информирован о выборе стратегии другим игроком;
5) допускается осреднение результатов игр.
Основная теорема теории игр Дж. фон Неймана: любая парная конечная игра с нулевой суммой имеет, по крайней мере, одно решение, возможно среди смешанных стратегий.
Отсюда следует, что каждая конечная игра имеет цену, которую обозначим через g, средний выигрыш, приходящийся на одну партию, удовлетворяющий условию a £ g £ b. Каждый игрок при многократном повторении игры, придерживаясь смешанных стратегий, получает более выгодный для себя результат. Оптимальное решение игры в смешанных стратегиях обладает следующим свойством: каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет оптимальную смешанную стратегию, так как это ему невыгодно.
Чистые стратегии игроков в их оптимальных смешанных стратегиях называются активными.
Теорема об активных стратегиях. Применение оптимальной смешанной стратегии обеспечивает игроку максимальный средний выигрыш (или минимальный средний проигрыш), равный цене игры g, независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий.
Смешанные стратегии игроков S1 и S2 обозначим соответственно A1 , A2 , … Am и B1 , B2 , B3 … Bn , а вероятности их использования через pA = (p1, p2, ..., pm) и qB = (q1, q2, ..., qn), где pi ³ 0, qj ³ 0, при этом 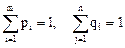 .
.
Тогда смешанная стратегия игрока I — SI, состоящая из стратегий A1, A2, ..., Am, имеет вид:
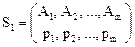 .
.
Соответственно для игрока II:
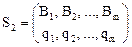 .
.
Зная матрицу А для игрока I можно определить средний выигрыш (математическое ожидание) 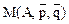 :
:
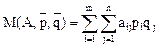 ,
,
Игрок I, применяя свои смешанные стратегии, стремится увеличить свой средний выигрыш, достигая
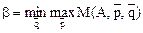 .
.
Игрок II добивается:
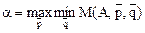 .
.
Обозначим через 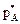 и
и 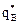 векторы, соответствующие оптимальным смешанным стратегиям игроков I и II, при которых выполняется равенство:
векторы, соответствующие оптимальным смешанным стратегиям игроков I и II, при которых выполняется равенство:
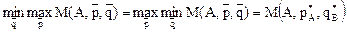 .
.
При этом выполняется условие:
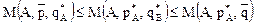
Решить игру — это означает найти цену игры и оптимальные стратегии.
Рассмотрим наиболее простой случай конечной игры 2 ´ 2 без седловой точки с матрицами:
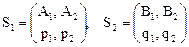 ,
,
С платежной матрицей
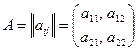 .
.
Требуется найти оптимальные смешанные стратегии игроков 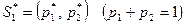 ,
, 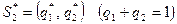 и цену игры g.
и цену игры g.
Каковы бы ни были действия противника, выигрыш будет равен цене игры g. Это означает, что если игрок I придерживается своей оптимальной стратегии 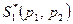 , то игроку II нет смысла отступать от своей оптимальной стратегии
, то игроку II нет смысла отступать от своей оптимальной стратегии 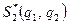 .
.
В игре 2 ´ 2, не имеющей седловой точки, обе стратегии являются активными.
Для игрока I имеем систему уравнений:
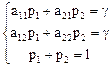
Для игрока II аналогично:
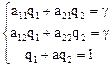
Если g ¹ 0 и игроки имеют только смешанные оптимальные стратегии, то определитель матрицы не равен нулю, следовательно, эти системы имеют единственное решение.
Решая систему уравнений (10) и (11) находим оптимальные ешения 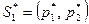 ,
, 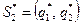 и g:
и g:
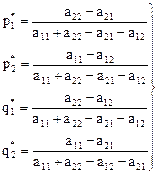
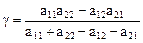
Пример: Дана платежная матрица:
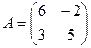
Найти решение.
Решение. Так как a = 3, b = 5, то a ¹ b, то и матрица игра не имеет седловой точки. Следовательно, решение ищем в смешанных стратегиях. Запишем системы уравнений:
для игрока I:
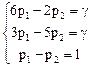
для игрока II:
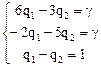
Решив эти системы находим:
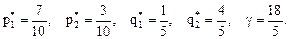
Следовательно оптимальные стратегии игроков имеют вид:
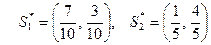 ,
,
3.5. Геометрический метод.
Решение игры в смешанных стратегиях допускает наглядную геометрическую интерпретацию. Геометрический метод решения игры включает следующие этапы.
1. В декартовой системе координат по оси абсцисс откладывается отрезок А1А2, длина которого равна 1 (рис. 2.1.). Левый конец отрезка точка x = 0 соответствует стратегии A1, правый, где х = 1,0 — стратегии А2. Все промежуточные точки этого отрезка соответствуют смешанным стратегиям S1 = (p1, p2).
2. По оси ординат от точки O откладываются выигрыши при стратегии А1.
3. На линии, параллельной оси ординат, от точки 1 откладываются выигрыши при стратегии А2 .
Пусть имеется игра с платежной матрицей:
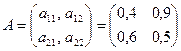 .
.
Если игрок II применяет стратегию В1, то выигрыш игрока I при использовании чистых стратегий А1 и А2 составляет соответственно a11 = 0,4 и a21 = 0,6. Соединим эти точки прямой В1В1 .
Если игрок I при стратегии В1 применяет смешанную стратегию 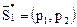 , то средний выигрыш, определяемый по формуле математического ожидания g1 = a11p1 + a21p2, изображается ординатой точки N на прямой B1B1. Прямая B1B1 называется стратегией В1. Ордината любой точки отрезка B1B1 равна величине выигрыша игрока I при применении им стратегии A1 и А2 с соответствующими вероятностями p1 и p2.
, то средний выигрыш, определяемый по формуле математического ожидания g1 = a11p1 + a21p2, изображается ординатой точки N на прямой B1B1. Прямая B1B1 называется стратегией В1. Ордината любой точки отрезка B1B1 равна величине выигрыша игрока I при применении им стратегии A1 и А2 с соответствующими вероятностями p1 и p2.
Аналогично строим отрезок В2В2 , сооветствующий применению игороком II с тратегии В2 .
Ординаты точек отрезка определяют средний стратегий А1 и А2 с соответствующими вероятностями p1 и p2 и равных g2 = a12p1 + a22p2.
Пример № 1. Найти оптимальную смешанную стратегию руководителя коммерческого предприятия и гарантированный средний выигрыш 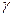 при выборе из двух новых технологий продажи товаров
при выборе из двух новых технологий продажи товаров 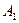 и
и 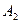 , если известны выигрыши каждого вида продажи по сравнению со старой технологией, которые представлены в виде матрицы игры.
, если известны выигрыши каждого вида продажи по сравнению со старой технологией, которые представлены в виде матрицы игры.
| Игрок II Игрок I | 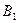 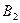 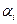
| ||
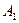
| 0,4 | 0,9 | 0,4 |
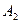
| 0,6 | 0,5 | 0,5 |
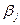
| 0,6 | 0,9 |
Решение: находим гарантированный выигрыш определяемый нижней ценой игры 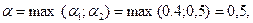 которая указывает на максиминную чистую стратегию
которая указывает на максиминную чистую стратегию 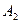 . Верхняя цена игры
. Верхняя цена игры 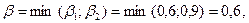 что свидетельствует об отсутствии седловой точки, т.к.
что свидетельствует об отсутствии седловой точки, т.к. 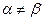 , тогда цена игры находиться в пределах
, тогда цена игры находиться в пределах 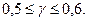 находим решение игры в смешанных стратегиях геометрическим методам рис. 2.1.
находим решение игры в смешанных стратегиях геометрическим методам рис. 2.1.
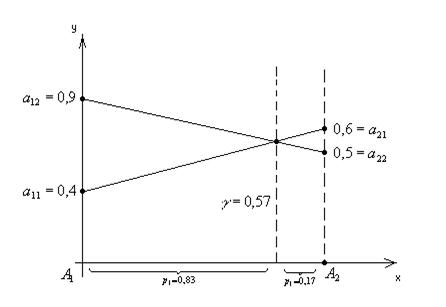
Рис. 2.1. Геометрический метод решения игры
Оптимальная смешанная стратегия и цена игры ровны.
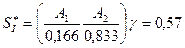

Гарантированный средний выигрыш составляет 0,57.
3.6. Метод линейного программирования.
Антагонистическую игру m ´ n (где m > 3, n > 3) с конечными значениями m и n можно свести к паре двойственных задач линейного программирования.
Рассмотрим игру m ´ n, заданную платежной матрицей:
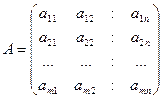 .
.
При постановке задач, необходимо иметь в виду некоторые преобразования, которые помогают упростить сложную задачу путем изменения – уменьшения размерности платежной матрицы посредством выделения и исключения доминирующих и дублирующих стратегий. Стратегия игрока Аi доминирует над стратегией Ак, если при любом поведении противника даст не меньший выигрыш, а если такой же, то дублирует Ак. В таком случае все элементы i строки больше (доминируют) или равны (дублируют) всех элементов строки k.
Пример. С учетом вариантов конъюнктуры В1, В2, В3, В4, В5 сложившейся на рынке и поведения покупателей в микрорайоне города коммерческое предприятие разработало шесть технологий продажи товаров А1, А2, А3, А4, А5, А6. Найти оптимальное решение. Возможные варианты среднедневного товарооборота в млн.руб. приведены в таблице:
| В1 | В2 | В3 | В4 | В5 | |
| А1 | 0,4 | 0,9 | 0,5 | 0,5 | 0,6 |
| А2 | 0,6 | 0,5 | 0,7 | 0,8 | 0,9 |
| А3 | 0,6 | 0,3 | 0,8 | 0,6 | 0,7 |
| А4 | 0,3 | 0,8 | 0,5 | 0,4 | 0,3 |
| А5 | 0,1 | 0,3 | 0,5 | 0,4 | 0,3 |
| А6 | 0,4 | 0,8 | 0,5 | 0,4 | 0,5 |
Стратегия А1 доминирует над стратегией А6, а стратегия А4 доминирует над стратегией А5, следовательно исключаем 5 и 6 строки матрицы
| В1 | В2 | В3 | В4 | В5 | |
| А1 | 0,4 | 0,9 | 0,5 | 0,5 | 0,6 |
| А2 | 0,6 | 0,5 | 0,7 | 0,8 | 0,9 |
| А3 | 0,6 | 0,3 | 0,8 | 0,6 | 0,7 |
| А4 | 0,3 | 0,8 | 0,5 | 0,4 | 0,3 |
С позиций проигрышей строки В стратегии В3, В4 и В5 доминируют над стратегией В1, поэтому эти столбцы исключаем из таблицы:
| В1 | В2 | |
| А1 | 0,4 | 0,9 |
| А2 | 0,6 | 0,5 |
| А3 | 0,6 | 0,3 |
| А4 | 0,3 | 0,8 |
С позиций игрока А стратегия А1 доминирует над стратегией А4, а стратегия А2 доминирует над стратегией А3, следовательно исключаем 3 и 4 строки матрицы:
| В1 | В2 | |
| А1 | 0,4 | 0,9 |
| А2 | 0,6 | 0,5 |
Допустим, что все элементы (выигрыши) платежной матрицы положительны (aij ³ 0) (если это не так, то можно ко всем элементам прибавлять достаточно большое число M, сделав их положительными. При этом цена игры увеличится на M, а решение задачи 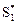 и
и 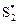 не изменится). Если все aij ³ 0, то g > 0. Пусть платежная матрица не содержит седловой точки, т.е. игра решается в смешанных стратегиях:
не изменится). Если все aij ³ 0, то g > 0. Пусть платежная матрица не содержит седловой точки, т.е. игра решается в смешанных стратегиях:
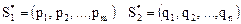 .
.
Применение игроком I оптимальной смешанной стратегии 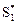 гарантирует ему средний выигрыш, не меньше цены игры g, независимо от поведения игрока II. Игрок II, применяя оптимальную смешанную стратегию
гарантирует ему средний выигрыш, не меньше цены игры g, независимо от поведения игрока II. Игрок II, применяя оптимальную смешанную стратегию 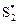 гарантирует для себя минимальный проигрыш (не больше g).
гарантирует для себя минимальный проигрыш (не больше g).
Если игрок II применяет свою чистую стратегию Bj, а игрок I — свою оптимальную стратегию 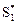 , то средний выигрыш игрока I равен:
, то средний выигрыш игрока I равен:
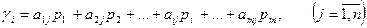
Если игрок I применяет чистую стратегию Аi, а игрок II – свою оптимальную смешанную стратегии 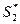 , то средний выигрыш игрока II составит
, то средний выигрыш игрока II составит
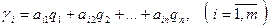
Учитывая, что gj не может быть меньше g для игрока I, а 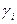 и не может быть больше g для игрока II, двойственную задачу линейного программирования можно записать следующим образом:
и не может быть больше g для игрока II, двойственную задачу линейного программирования можно записать следующим образом:
1) для игрока I:
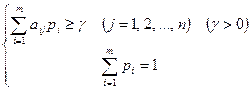
2) для игрока II:
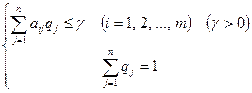
Смысл этих систем уравнений заключается в следующем: игрок I стремится увеличить цену игры (g ® max), он действует так, чтобы его средний выигрыш при использовании его стратегий с вероятностями pi для любой j-й стратегии игрока II был не меньше величины g, которую он стремится увеличить. Игрок II с
| <== предыдущая страница | | | следующая страница ==> |
| Глава I. Линейное программирование | | | Определение неприступного расстояния |
Дата добавления: 2014-10-14; просмотров: 487; Нарушение авторских прав

Мы поможем в написании ваших работ!