
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Глава I. Линейное программирование
|
Читайте также: |
1.1. Примеры задач линейного программирования.
Пример 1. Пусть малое предприятие «Стакан» продает два вида прохладительных напитков, скажем, «Колокольчик» и «Буратино». Оба напитка изготавливаются тут же на месте из имеющихся запасов газированной воды, фруктового сиропа, лимонной кислоты и льда. Нормы расхода сырья на одну порцию готовой продукции и его запасы приведем для удобства в виде таблицы.
| Виды сырья | Нормы расхода сырья на 1 порцию продукции | Запасы сырья на одни сутки | |
| Колокольчик | Буратино | ||
| Газированная вода | 0,450 л. | 0,48 л. | 900 л. |
| Фруктовый сироп | 0,050 л. | 0,020 л. | 80 л. |
| Лимонная кислота | 0,001 л. | 0,002 л. | 12 л. |
| Лед в кубиках по 10 г. | 20 г. | 30 г. | 20 кг. |
Допустим, что одна проданная порция «Колокольчика» приносит предприятию 5 рублей прибыли, порция «Буратино» - 6 рублей. Также предположим, что нет никаких проблем с изготовлением необходимого количества порций напитков и, что спрос перекрывает предложение.
Возникает вполне естественный вопрос - сколько порций того и другого напитка следует произвести из имеющегося сырья, чтобы получить максимальную прибыль?
Составим математическую модель данной задачи.
Во-первых, введем переменные. Пусть 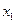 - количество порций «Колокольчика», которое следует произвести, а
- количество порций «Колокольчика», которое следует произвести, а 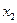 - количество порций «Буратино».
- количество порций «Буратино».
Во-вторых, введем оптимизируемую целевую функцию, в данном случае прибыль: F 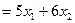 .
.
Тот факт, что следует найти максимум, функции  запишем следующим образом:
запишем следующим образом:
F 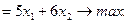 (1)
(1)
В-третьих, запишем имеющиеся (нетривиальные) ограничения по сырью, вытекающие из того, что объем израсходованного на производство напитков сырья не превышает его суточного запаса.
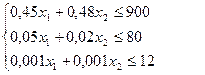 (2)
(2)
Добавим сюда тривиальные (очевидные) ограничения:
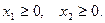 (3)
(3)
Условие (1) вместе с ограничениями (2), (3) и дают требуемую математическую модель, которая является частным случаем задачи линейного программирования (см. п. 1.2.).
Как мы увидим позже, модель примера №1 является однородной задачей линейного программирования (см. п. 1.3.).
Дадим обобщение примера №1.
Пример 2. Пусть предприятие выпускает к-типов продукции, используя т-видов ресурсов. При этом расход i-го вида ресурса на единицу j-го вида продукции составляют 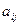 ; всего имеется объем
; всего имеется объем 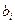 запаса i-го вида ресурса; реализация единицы продукции j-го вида дает
запаса i-го вида ресурса; реализация единицы продукции j-го вида дает 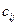 условных денежных единиц прибыли. Требуется составить оптимальный план выпуска продукции.
условных денежных единиц прибыли. Требуется составить оптимальный план выпуска продукции.
Модель задачи имеет в этом случае вид:
F 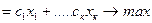
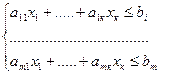
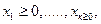
где 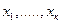 - объемы планируемого выпуска продукции.
- объемы планируемого выпуска продукции.
1.2. Постановка задачи линейного программирования. Основные понятия.
Определение 1. Задача линейного программирования состоит в оптимизации линейной функции, зависящей от конечного числа вещественных переменных, при заданной системе линейных ограничений (имеющих вид равенства или неравенства).
Определение 2. Зависящая от 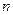 переменных
переменных 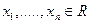 функция
функция 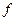 называется линейной, если она имеет вид:
называется линейной, если она имеет вид: 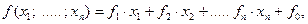 где
где 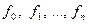 - некоторые фиксированные вещественные коэффициенты.
- некоторые фиксированные вещественные коэффициенты.
Пусть 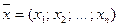
и
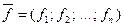 .
.
Тогда
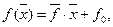
где
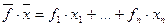
- скалярное произведение векторов в n-мерном арифметическом пространстве 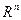 . Напомним, что n-мерным арифметическим пространством
. Напомним, что n-мерным арифметическим пространством 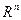 называется множество всех упорядоченных наборов n вещественных чисел (
называется множество всех упорядоченных наборов n вещественных чисел ( 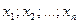 ) с операциями умножения на числа
) с операциями умножения на числа 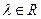 и сложения, определенными по-координатно:
и сложения, определенными по-координатно:
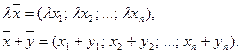
Элементы пространства 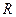 n называются векторами, а само пространство – векторным или линейным.
n называются векторами, а само пространство – векторным или линейным.
Определение 3. Ограничения вида:
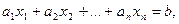
или
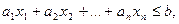
или
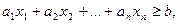
называются линейными.
Если положить 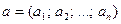 , то можно записать эти ограничения в векторном виде:
, то можно записать эти ограничения в векторном виде:
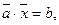
или
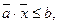
или
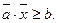
Другими словами, ограничение, имеющее вид равенства или неравенства, называется линейным, если справа стоит константа, а слева – линейная функция.
Определение 4. Ограничения вида: 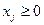 или
или 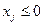
- называются тривиальными.
Эти ограничения записывают обычно в конце системы ограничений задачи линейного программирования (ЛП). Все остальные ограничения называются нетривиальными.
Таким образом, общая задача ЛП может быть представлена в виде: 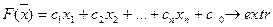
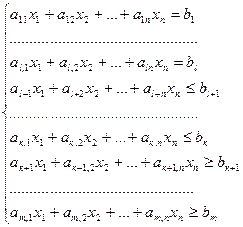 (1)
(1)
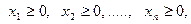
Здесь запись 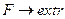 означает, что следует найти экстремум, то есть максимум (max) или минимум (min), функции F.
означает, что следует найти экстремум, то есть максимум (max) или минимум (min), функции F.
Определение 5. Оптимизируемая в задаче ЛП функции F называется целевой функцией этой задачи.
Итак, задача ЛП определяется оптимизируемой линейной целевой функцией, нетривиальными линейными ограничениями типа равенства или неравенства и тривиальными ограничениям (которые могут отсутствовать).
Обозначение: Для сокращения записи будем далее писать  если
если 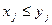 для всех
для всех 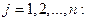
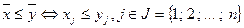
В векторном виде задача (1) имеет вид:
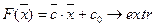
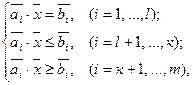 (2)
(2)
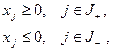
где 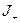 и
и 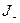 - некоторые непересекающиеся подмножества множества индексов
- некоторые непересекающиеся подмножества множества индексов 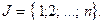
Определение 6. Матрица А= 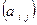 , составленная из коэффициентов
, составленная из коэффициентов 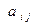 системы ограничений, называется матрицей системы ограничений, а столбец
системы ограничений, называется матрицей системы ограничений, а столбец 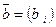 - столбцом свободных членов.
- столбцом свободных членов.
Заметим, что матрица А имеет размеры m  n , то есть состоит из m строки n столбцов, а вектор
n , то есть состоит из m строки n столбцов, а вектор 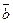 состоит из одного столбца. Отметим, что вектор переменных
состоит из одного столбца. Отметим, что вектор переменных 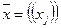 состоит из одной строки (или столбца).
состоит из одной строки (или столбца).
Определение 7. Вектор 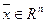 называется возможным решением задачи ЛП, если он удовлетворяет всем нетривиальным ограничениям.
называется возможным решением задачи ЛП, если он удовлетворяет всем нетривиальным ограничениям.
Определение 8. Вектор 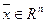 называется допустимым решением задачи ЛП, если он удовлетворяет всем ограничениям задачи ЛП, включая тривиальные.
называется допустимым решением задачи ЛП, если он удовлетворяет всем ограничениям задачи ЛП, включая тривиальные.
Определение 9. Множество всех допустимых решений образует область допустимых решений (ОДР) задачи ЛП.
Определение 10. Вектор 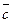 коэффициентов
коэффициентов 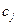 при переменных
при переменных 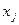 целевой функции F называется вектором роста целевой функции:
целевой функции F называется вектором роста целевой функции: 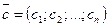
Определение 11. Свободный член 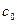 целевой функции
целевой функции 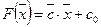 называется начальным значением целевой функции.
называется начальным значением целевой функции.
Ясно, что 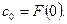
Определение 12. Допустимое решение 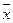 называется оптимальным, если целевая функция F достигает на
называется оптимальным, если целевая функция F достигает на 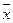 своего экстремума (максимума или минимума) в области допустимых решений.
своего экстремума (максимума или минимума) в области допустимых решений.
Смысл названия «вектор роста» становится ясным, если заметить, что вектор 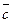 является градиентом функции F, то есть вектором, составленным из частных производных функции F. Действительно, если мы продифференцируем линейную функцию
является градиентом функции F, то есть вектором, составленным из частных производных функции F. Действительно, если мы продифференцируем линейную функцию
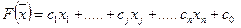
по переменной 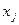 , считая остальные переменные постоянными, то конечно получим
, считая остальные переменные постоянными, то конечно получим 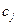 :
:
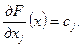 (3)
(3)
Как известно из анализа, градиент функции  указывает направление максимального роста функции в данной точке. Из (3) видно, что в линейном случае это направление не зависит от точки
указывает направление максимального роста функции в данной точке. Из (3) видно, что в линейном случае это направление не зависит от точки 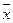 и совпадает с направлением вектора
и совпадает с направлением вектора 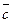 .
.
Определение 13. Линией (на плоскости) или поверхностью (в пространстве) уровня функции 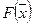 называется множество точек
называется множество точек 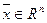 , удовлетворяющих равенству:
, удовлетворяющих равенству:
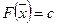 ,
,
где с – некоторая произвольная константа.
1.3. Различные формы задачи ЛП
Помимо общей задачи ЛП, выделяют однородную, каноническую и симплексную формы задачи ЛП.
Определение 1. Задача ЛП называется однородной, если все ограничения имеют вид неравенства.
Частными случаями однородной задачи являются задача о ресурсах (или производственная):
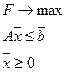 (1)
(1)
и задача об издержках:
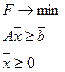 (2)
(2)
В первом случае требуется найти максимум функции F («прибыли») при ограниченных «ресурсах» 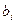 , во втором – минимум издержек F при заданных «нормах потребления»
, во втором – минимум издержек F при заданных «нормах потребления» 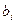 , Более подробно, эти типы задачи ЛП будут рассмотрены в следующих параграфах.
, Более подробно, эти типы задачи ЛП будут рассмотрены в следующих параграфах.
Определение 2. Задача ЛП называется канонической, если все нетривиальные ограничения имеют вид равенства и на все переменные наложены тривиальные ограничения.
Поскольку, переменную 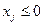 можно заменить на новую переменную
можно заменить на новую переменную 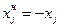 , удовлетворяющую условию
, удовлетворяющую условию 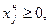 то, без ограничения общности, можно считать, что все переменные канонической задачи ЛП неотрицательны.
то, без ограничения общности, можно считать, что все переменные канонической задачи ЛП неотрицательны.
Таким образом, каноническая задача ЛП может быть записана в виде:
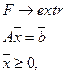 (3)
(3)
или в координатной форме:
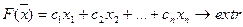
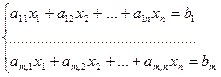 (4)
(4)
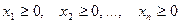
Определение 3. Каноническая задача ЛП называется симплексной, если:
1) система линейных ограничений имеет разрешенный вид, то есть матрица системы  содержит единичную матрицу
содержит единичную матрицу 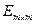 ;
;
2) столбец свободных членов 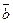 неотрицателен:
неотрицателен: 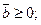
3) целевая функция F зависит только от свободных переменных.
Разъясним смысл некоторых терминов, встречающихся в этом определении. Во-первых, напомним, что матрица размера т´т называется единичной (и обозначается Е=Е 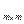 ), если:
), если:
1) 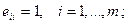
2) 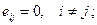
Например, единичными называются матрицы:
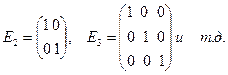
Во-вторых, говорят, что система линейных уравнений (4) имеет разрешенный вид, если ее матрица содержит, возможно после перестановки столбцов, единичную подматрицу Е размера т  т. Столбцы единичной подматрицы имеют вид:
т. Столбцы единичной подматрицы имеют вид:
 и называются базисными.
и называются базисными.
Определение 4. Переменные, соответствующие базисным столбцам, называются также базисными, а остальные переменные – свободными.
Если исходная матрица системы (4) содержит т линейно независимых строк (или столбцов), то есть ее ранг равен т, то, как известно, с помощью метода Гаусса система может быть приведена к равносильной системе, имеющей разрешенный вид. При этом в качестве базисных могут быть выбраны любые т линейно независимых столбцов исходной системы.
Напомним, что метод Гаусса состоит в приведении матрицы системы к ступенчатому виду с помощью элементарных преобразований, к которым относятся:
1) перестановка строк;
2) умножение строки на число 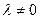 ;
;
3) замена одной из строк ее суммой с другой строкой, умноженой на некоторое произвольное число 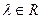 .
.
Как правило, базисными будем считать последние т столбцов матрицы системы.
Замечание: Далее слова «матрица системы А содержит единичную подматрицу» будут означать, что матрица системы А после перестановки столбцов содержит единичную подматрицу Е размера т  т, где т – число строк матрицы А.
т, где т – число строк матрицы А.
Определение 5. Решение системы (4) называется базисным, если все свободные переменные равны нулю.
Определение 6. Допустимое базисное решение называется опорным решением.
Напомним, что вектор 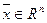 называется допустимым решением, если он удовлетворяет как нетривиальным ограничениям, в данном случае системе уравнений (4), так и тривиальным:
называется допустимым решением, если он удовлетворяет как нетривиальным ограничениям, в данном случае системе уравнений (4), так и тривиальным:
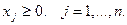
Таким образом решение 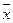 системы (4) оказывается допустимым, если все его компоненты
системы (4) оказывается допустимым, если все его компоненты 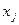 неотрицательны.
неотрицательны.
В дальнейшем будет показано, что оптимальное решение канонической задачи ЛП является опорным.
1.4. Связь между различными типами задачи ЛП.
Покажем, что общая задача ЛП может быть сведена как к однородной задаче ЛП, так и к канонической.
I. Вначале сведём общую задачу к однородной. В соответствии с определением 1 п.1.3 для этого достаточно каждое ограничение вида равенства:
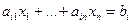 ,
,
заменить на равносильную систему неравенств:
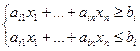
Все ограничения задачи будут иметь вид неравенства и задача станет однородной. При этом число ограничений, конечно же, увеличится.
II. Теперь сведем общую задачу ЛП к канонической. Для этого следует, во-первых, представить каждое неравенство в виде равенства и, во-вторых, добиться того, чтобы все переменные задачи были неотрицательны. Для каждого неравенства системы ограничений вида «меньше»
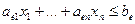 ,
,
добавим новую (балансовую) переменную 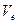 , определяемую равенством:
, определяемую равенством:
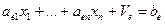 .
.
Для каждого неравенства системы ограничений вида «больше»
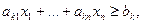
введем переменную 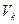 , определяемую равенством:
, определяемую равенством:
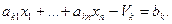
Ясно, что так определенные балансовые переменные 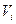 неотрицательны. Таким способом все неравенства могут быть заменены на равенства.
неотрицательны. Таким способом все неравенства могут быть заменены на равенства.
Для каждой переменной 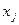 , на которую не наложено тривиальное ограничение, положим:
, на которую не наложено тривиальное ограничение, положим: 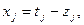 где
где 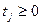 и
и 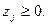
Заменив все такие 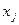 на
на 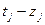 , получим эквивалентную задачу, в которой все переменные неотрицательны. Поскольку ранее мы уже добились того, что все ограничения задачи имеют вид равенства, то полученная задача оказывается канонической.
, получим эквивалентную задачу, в которой все переменные неотрицательны. Поскольку ранее мы уже добились того, что все ограничения задачи имеют вид равенства, то полученная задача оказывается канонической.
Пример 1. Пусть дана задача ЛП
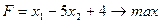
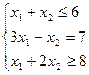 (1)
(1)
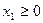
Требуется преобразовать исходную общую задачу ЛП к другим формам задачи ЛП.
1. Сведем эту задачу к однородной форме.
Заменяя равенство из (1) на систему неравенств получим соответствующую однородную задачу:
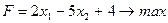
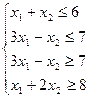 (2)
(2)
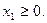
2. Сведем задачу к каноничной форме. Добавим неотрицательные балансовые переменные 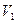 и
и 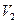 , превращая первое и третье ограничения в равенства:
, превращая первое и третье ограничения в равенства:
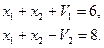
Заменим переменную 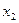 :
:
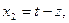
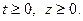
Тогда получим каноническую задачу:
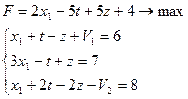 (3)
(3)
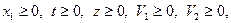
фактически равносильную исходной.
Таким образом, показано, что общая, однородная и канонические формы задачи ЛП могут быть сведены друг к другу.
Сведение произвольной канонической задачи ЛП к симплексной форме будет рассмотрено в следующих параграфах.
Укажем на один частный случай сведения однородной задачи ЛП к симплексной форме. Пусть дана задача о ресурсах, то есть однородная задача ЛП вида:
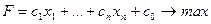
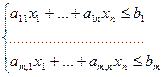 (4)
(4)
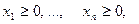
причем все 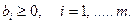
Сведем эту задачу к канонической с помощью введения балансовых переменных 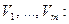
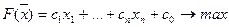
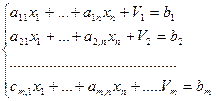 (5)
(5)
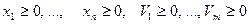
Полученная каноническая задача ЛП на самом деле является симплексной, поскольку, во-первых, столбец свободных членов 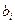 состоит только из неотрицательных элементов, во-вторых, система уравнений имеет разрешенный вид (столбцы переменных
состоит только из неотрицательных элементов, во-вторых, система уравнений имеет разрешенный вид (столбцы переменных 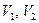 , …,
, …, 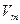 и сами переменные являются базисными), в-третьих, целевая функция F зависит только от свободных переменных
и сами переменные являются базисными), в-третьих, целевая функция F зависит только от свободных переменных 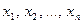 .
.
1.5. Графический метод решения задачи ЛП.
Рассмотрим графический метод решения однородной двумерной задачи ЛП на конкретном примере.
Пример №1.
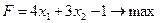
Решение. Найдем вначале область допустимых решений (ОДР). Решим графически первое неравенство:
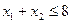 (1)
(1)
Для этого построим вначале прямую линию, соответствующую уравнению:
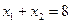 . (11)
. (11)
Поскольку, если 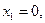 то
то 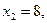 то прямая (11) проходит через точку М1(0;8). Аналогично, если
то прямая (11) проходит через точку М1(0;8). Аналогично, если 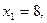 то
то 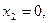 и прямая (11) проходит также через точку М2 (8;0). Проведем через эти две точки прямую линию и отметим ее с помощью 1 (см. рис. 1). Эта линия делит плоскость на две полуплоскости, которые мы условно назовем верхней и нижней полуплоскостями. Так как координаты точки (0;0) удовлетворяют неравенству (1), то этому неравенству соответствует нижняя полуплоскость, которая содержит эту точку. Этот факт мы изобразим на рис. 1 штрихами, направленными вниз от линии 1 .
и прямая (11) проходит также через точку М2 (8;0). Проведем через эти две точки прямую линию и отметим ее с помощью 1 (см. рис. 1). Эта линия делит плоскость на две полуплоскости, которые мы условно назовем верхней и нижней полуплоскостями. Так как координаты точки (0;0) удовлетворяют неравенству (1), то этому неравенству соответствует нижняя полуплоскость, которая содержит эту точку. Этот факт мы изобразим на рис. 1 штрихами, направленными вниз от линии 1 .
Теперь решим графически второе неравенство:
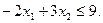 (2)
(2)
Ему соответствует прямая, заданная уравнением:
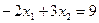 (21)
(21)
Ее мы построим несколько иначе. Перепишем уравнение (21) в виде:
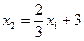
Тогда при 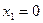 оказывается
оказывается 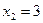 , что дает точку М3 (0;3) искомой прямой. Угловой коэффициент этой прямой
, что дает точку М3 (0;3) искомой прямой. Угловой коэффициент этой прямой 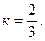 Но угловой коэффициент любой прямой равен
Но угловой коэффициент любой прямой равен 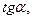 где
где 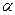 - угол наклона прямой к оси 0х:
- угол наклона прямой к оси 0х: 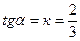 . Если теперь мы отложим три единицы вправо от точки М3 (0;3) и затем две единицы вверх, то получим другую точку М4 (3;5) которая также лежит на прямой (21). Через точки М3 и М4 мы проводим прямую 2 (рис.1). Начало координат (0;0) удовлетворяет (2) и лежит ниже графика линии 2 , поэтому соответствующая полуплоскость является «нижней», что мы и отмечаем штрихами, направленными вниз от прямой 2 (рис.1). Аналогично строим прямую 3.
. Если теперь мы отложим три единицы вправо от точки М3 (0;3) и затем две единицы вверх, то получим другую точку М4 (3;5) которая также лежит на прямой (21). Через точки М3 и М4 мы проводим прямую 2 (рис.1). Начало координат (0;0) удовлетворяет (2) и лежит ниже графика линии 2 , поэтому соответствующая полуплоскость является «нижней», что мы и отмечаем штрихами, направленными вниз от прямой 2 (рис.1). Аналогично строим прямую 3.
Уравнение
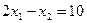 (3)
(3)
заменяем на уравнение
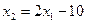 ,
,
Ясно, что прямая проходит через т. М5 (5;0), и имеет угловой коэффициент к = 2. При этом самому неравенству
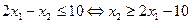
соответствует верхняя полуплоскость, отмеченная штрихами вверх от прямой (3).
Тривиальному неравенству 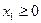 соответствует правая полуплоскость координатной плоскости, то есть полуплоскость, лежащая справа от вертикальной оси
соответствует правая полуплоскость координатной плоскости, то есть полуплоскость, лежащая справа от вертикальной оси 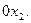 Ее отмечаем штрихами, направленными вправо от оси 0
Ее отмечаем штрихами, направленными вправо от оси 0 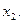 Наконец неравенству
Наконец неравенству 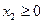 соответствует верхняя полуплоскость координатной плоскости, отмеченная штрихами, направленными вверх от оси 0
соответствует верхняя полуплоскость координатной плоскости, отмеченная штрихами, направленными вверх от оси 0 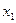 . Пересечение всех указанных полуплоскостей определяет ОДР данной задачи. На рисунке 1 это область, ограниченная выпуклым пятиугольником ОАВСD.
. Пересечение всех указанных полуплоскостей определяет ОДР данной задачи. На рисунке 1 это область, ограниченная выпуклым пятиугольником ОАВСD.
Изобразим на рисунке 1 вектор роста 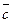 целевой функции
целевой функции  . Это вектор
. Это вектор 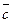 началом в т. (0;0) и концом в точке М (4;3), поскольку
началом в т. (0;0) и концом в точке М (4;3), поскольку 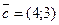 .
.
Построим теперь линию уровня 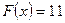 . Она определяется уравнением:
. Она определяется уравнением:
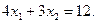 (3)
(3)
Мы взяли здесь константу С =11, для того чтобы точки пересечения прямой (3) с осями  имели целые координаты. Действительно, если
имели целые координаты. Действительно, если 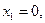 то
то 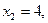 и, если
и, если 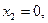 то
то 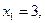 что дает две точки М1 (0;4) и М2 (3;0) линии уровня (3). Через них проводим пунктиром соответствующую линию уровня (рис. 1). Она оказывается перпендикулярна вектору роста
что дает две точки М1 (0;4) и М2 (3;0) линии уровня (3). Через них проводим пунктиром соответствующую линию уровня (рис. 1). Она оказывается перпендикулярна вектору роста 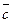 . Отрезок
. Отрезок 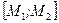 пересекается с ОДР и в каждой его точке х значение целевой функции
пересекается с ОДР и в каждой его точке х значение целевой функции 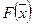 равно 11:
равно 11:
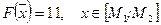 .
.
Мы знаем, что значение функции F увеличивается в направлении вектора роста 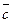 . Чтобы найти максимальное значение
. Чтобы найти максимальное значение 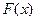 на ОДР будем параллельно перемещать линию уровня в направлении вектора роста
на ОДР будем параллельно перемещать линию уровня в направлении вектора роста 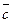 до тех пор, пока, она будет иметь хотя бы одну точку пересечения с ОДР задачи. Из рисунка 1 ясно, что последнее пересечение смещенной линии уровня (3) будет точка
до тех пор, пока, она будет иметь хотя бы одну точку пересечения с ОДР задачи. Из рисунка 1 ясно, что последнее пересечение смещенной линии уровня (3) будет точка 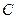
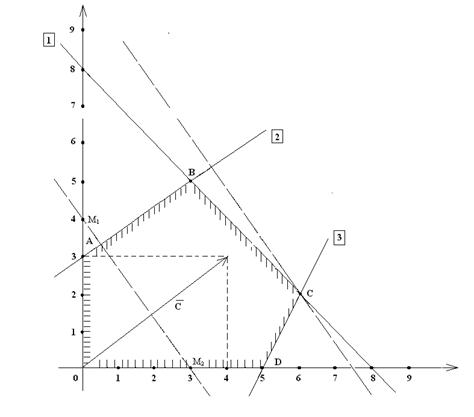 Рисунок 1. Графическое решение задачи ЛП.
Рисунок 1. Графическое решение задачи ЛП.
На этой линии очевидно и будет достигаться максимальное значение целевой функции F в ОДР, поскольку при дальнейшем движении линии уровня в направлении вектора роста, она перестает пересекаться с ОДР. Итак, максимальное значение функция F(х) имеет в точке 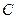 . Так как точка
. Так как точка 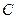 является пересечением прямых 1 и 3, то ее координаты находятся из системы:
является пересечением прямых 1 и 3, то ее координаты находятся из системы:
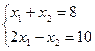 (4)
(4)
Чтобы решить эту систему, сложим оба уровня. Тогда получим, что 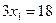 или
или 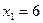 .
.
Из первого уравнения находим, что 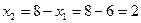
Итак, координаты точки С найдены – С (6;2). Найдем максимальное значение функции:
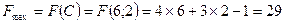
Задача решена
Ответ: максимальное значение целевой функции F достигается в точке С (6;2) и равно 29:
 .
.
1.6. Выпуклые множества на плоскости и в пространстве.
Определение 1. Множество А 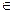 Rn называется выпуклым, если с любыми своими двумя точками
Rn называется выпуклым, если с любыми своими двумя точками 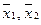
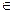 А оно содержит целиком отрезок
А оно содержит целиком отрезок 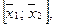 их соединяющий:
их соединяющий:
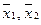
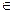 А
А 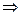
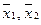
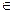 А. (1)
А. (1)
Пусть 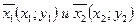 два вектора на плоскости х О у и пусть точка
два вектора на плоскости х О у и пусть точка 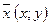 лежит на отрезке
лежит на отрезке 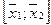 . Тогда вектор
. Тогда вектор 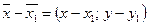 колинеарен вектору
колинеарен вектору 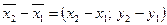 , направлен в одну сторону с ним и не превосходит его по длине. Эти условия могут быть записаны в виде равенства:
, направлен в одну сторону с ним и не превосходит его по длине. Эти условия могут быть записаны в виде равенства:
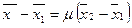 , (2)
, (2)
где 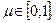
Векторное равенство (2) равносильно системе:
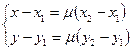 (3)
(3)
Система (3) может быть преобразована в равносильную систему:
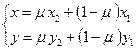 (4)
(4)
где 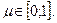 Обозначим
Обозначим 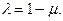 Тогда (4) примет вид:
Тогда (4) примет вид:
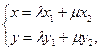 (5)
(5)
где
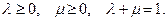
В векторном виде система (5) примет вид:
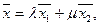
где 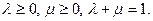 (6)
(6)
Определение 2. Выпуклой (линейной) комбинацией векторов 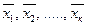 называется выражение вида:
называется выражение вида:
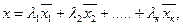
где все 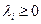 и
и 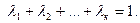
Равенство (6) показывает, что каждая точка 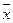 отрезка
отрезка 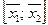 является выпуклой комбинацией векторов
является выпуклой комбинацией векторов 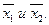
Теорема 1. Пересечение любого числа выпуклых множеств является выпуклым множеством.
Доказательство. Пусть 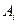 - любое семейство выпуклых множеств. Пусть А – их пересечение:
- любое семейство выпуклых множеств. Пусть А – их пересечение: 
Покажем, что множество А – выпукло. Пусть 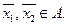 Тогда
Тогда 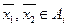 для каждого
для каждого 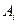 , поскольку А – пересечение всех
, поскольку А – пересечение всех 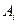 . Так как
. Так как 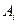 - выпукло, то вместе с точками
- выпукло, то вместе с точками 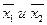 оно содержит и соединяющий их отрезок:
оно содержит и соединяющий их отрезок:
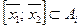 для всех Аi.
для всех Аi.
Но, отсюда, очевидно, следует, что каждая точка отрезка 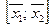 (а значит и сам отрезок) принадлежит пересечению множеств
(а значит и сам отрезок) принадлежит пересечению множеств 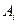 , то есть множеству А. Итак, А – выпуклое множество. Что и требовалось доказать.
, то есть множеству А. Итак, А – выпуклое множество. Что и требовалось доказать.
Определение 3. Выпуклой оболочкой множества 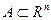 называется такое выпуклое множество
называется такое выпуклое множество 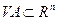 , что:
, что:
1) 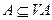 ,
,
2)  - выпукло
- выпукло 
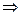
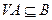 .
.
Лемма 1. Выпуклая оболочка множества А совпадает с пересечением всех выпуклых множеств, содержащих А.
Доказательство. Пусть В0 – пересечение всех выпуклых множеств, содержащих А. Тогда очевидно В0, содержит А. С другой стороны по теореме 1 множество В0 само выпукло. Отсюда следует, что В0= VA, поскольку выполнены свойства 1) и 2).
Лемма 2. Отрезок 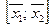 является выпуклой оболочкой своих концов
является выпуклой оболочкой своих концов 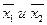 .
.
Доказательство. Пусть  , то есть множество А состоит из двух элементов
, то есть множество А состоит из двух элементов 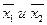 . Отрезок
. Отрезок 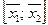 является выпуклым множеством и содержит А. С другой стороны каждое выпуклое множество В, содержащее А, содержит по определению выпуклости и весь отрезок
является выпуклым множеством и содержит А. С другой стороны каждое выпуклое множество В, содержащее А, содержит по определению выпуклости и весь отрезок 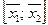 . Тем самым показано, что
. Тем самым показано, что 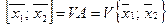 ч т.д.
ч т.д.
Лемма 3. Если выпуклое множество 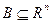 содержит векторы
содержит векторы 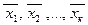 , то оно содержит и любую их выпуклую комбинацию:
, то оно содержит и любую их выпуклую комбинацию:
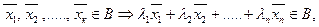
где 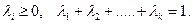
Доказательство. Докажем это по индукции. Для двух точек 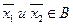 утверждение леммы практически было доказано выше, поскольку множество выпуклых комбинаций
утверждение леммы практически было доказано выше, поскольку множество выпуклых комбинаций 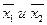 совпадает с отрезком
совпадает с отрезком 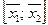 и, следовательно, содержится в В. Пусть утверждение справедливо для всех
и, следовательно, содержится в В. Пусть утверждение справедливо для всех 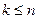 . Покажем, что оно будет также справедливым и для
. Покажем, что оно будет также справедливым и для 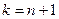 .
.
Пусть 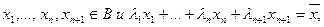 где
где
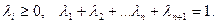
Пусть
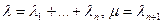
и 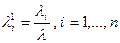 .
.
Тогда
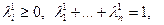
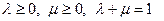
и
 где
где 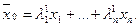 По предположению индукции
По предположению индукции 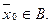 Так как
Так как 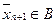 и
и 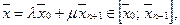 то
то 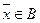 . Лемма доказана.
. Лемма доказана.
Теорема 2. Выпуклая оболочка VA множества А 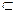 Rn совпадает с множеством всех выпуклых комбинаций, состоящих из конечного числа векторов множества А.
Rn совпадает с множеством всех выпуклых комбинаций, состоящих из конечного числа векторов множества А.
Доказательство: Пусть В0 – множество всех таких комбинаций векторов множества А. Как следует из леммы 3 множество В0 содержится в любом выпуклом множестве В, содержащем А. Осталось показать, что само В0 – выпукло.
Пусть 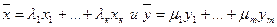 - два вектора множества В0. Тогда
- два вектора множества В0. Тогда 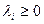 ,
, 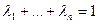 ,
, 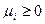 ,
, 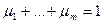 .
.
Пусть - 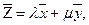 где
где 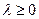 и
и 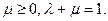 Достаточно показать, что
Достаточно показать, что 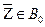 , то есть что вектор
, то есть что вектор 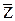 сам является выпуклой комбинацией векторов из А0. Но это верно, поскольку:
сам является выпуклой комбинацией векторов из А0. Но это верно, поскольку:
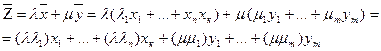
- выпуклая комбинация векторов 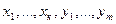 - так как
- так как 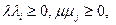 и
и 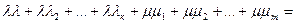
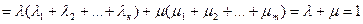 ч.т.д.
ч.т.д.
Отметим, что треугольник и пирамида являются выпуклыми оболочками своих вершин, и, следовательно, каждая их точка является выпуклой комбинацией векторов-вершин.
Определение. Выпуклая оболочка 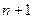 точки в
точки в 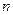 - мерном линейном пространстве
- мерном линейном пространстве 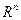 называется симплексом.
называется симплексом.
Предполагается, что точки лежат в общем положении, то есть не содержатся ни в какой гиперплоскости.
Рассмотрим некоторую точку 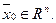 Возможны следующие случаи расположения точки
Возможны следующие случаи расположения точки 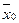 относительно множества В.
относительно множества В.
Первый случай. На каждой прямой l , проходящей через 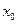 , можно найти отрезок
, можно найти отрезок  , лежащий целиком в В и содержащий
, лежащий целиком в В и содержащий 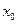 внутри себя:
внутри себя:
1) 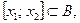
2) 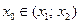 . (7)
. (7)
Второй случай. Существует содержащая 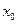 прямая
прямая  , на которой не существует отрезка
, на которой не существует отрезка 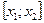 , удовлетворяющего (7).
, удовлетворяющего (7).
Если 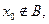 то ясно, что свойством (7) не обладает ни один отрезок
то ясно, что свойством (7) не обладает ни один отрезок 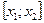 . Если для некоторых прямых проходящих через точку
. Если для некоторых прямых проходящих через точку 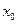 отрезок удовлетворяющий (7), существует, а для других прямых нет, то
отрезок удовлетворяющий (7), существует, а для других прямых нет, то 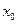 называется граничной точкой множества В. Вблизи граничной точки
называется граничной точкой множества В. Вблизи граничной точки 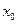 лежат как точки множества В, так и точки ему не принадлежащие.
лежат как точки множества В, так и точки ему не принадлежащие.
Третий случай.
Определение. Пусть точка 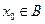 и ни для одной прямой l содержащей
и ни для одной прямой l содержащей 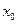 , не существует отрезка
, не существует отрезка 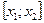 , удовлетворяющего (7). В этом случае
, удовлетворяющего (7). В этом случае 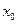 называется угловой точкой множества В.
называется угловой точкой множества В.
Другими словами любой отрезок, содержащий угловую точку 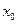 внутри себя, обязательно «высовывается» из множества В.
внутри себя, обязательно «высовывается» из множества В.
Замечание.
Условие 2) Из (7) можно заменить в предыдущих рассуждениях на условие: 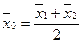 , - то есть можно считать, без ограничения общности, что точка
, - то есть можно считать, без ограничения общности, что точка 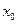 является серединой отрезка
является серединой отрезка 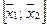 , действительно, если существует отрезок, содержащий
, действительно, если существует отрезок, содержащий 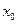 внутри себя, то существует в нем меньший отрезок, для которого точка
внутри себя, то существует в нем меньший отрезок, для которого точка 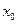 является серединой.
является серединой.
Определение. Множество 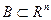 называется замкнутым, если оно содержит все свои граничные точки.
называется замкнутым, если оно содержит все свои граничные точки.
Значение угловых точек для описания выпуклого множества в 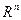 дает следующая теорема, которую мы приводим без доказательства.
дает следующая теорема, которую мы приводим без доказательства.
Теорема 3. Замкнутое выпуклое множество 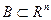 является выпуклой оболочкой своих угловых точек.
является выпуклой оболочкой своих угловых точек.
1.7. Геометрическая интерпретация однородной задачи линейного программирования.
Рассмотрим вначале однородную задачу линейного программирования на плоскости.
Каждому ограничению вида неравенства:
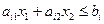 , (1)
, (1)
- соответствует замкнутая полуплоскость 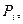 границей, которой является прямая линия
границей, которой является прямая линия 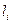 , определяемая соответствующим уравнением:
, определяемая соответствующим уравнением:
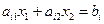 . (2)
. (2)
Системе ограничений однородной задачи:
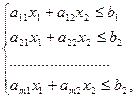 (3)
(3)
- соответствует пересечение полуплоскостей 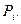 Тривиальным ограничениям:
Тривиальным ограничениям:
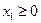 и
и 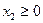 , (4)
, (4)
- также соответствуют полуплоскости 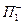 и
и 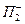
При этом 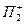 называют, обычно, верхней (координатной) полуплоскостью, а
называют, обычно, верхней (координатной) полуплоскостью, а 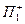 - правой (координатной) полуплоскостью.
- правой (координатной) полуплоскостью.
Таким образом, ОДР однородной задачи ЛП на плоскости представляет из себя пересечение конечного числа замкнутых полуплоскостей.
Очевидно, каждая полуплоскость является выпуклым множеством. По теореме 1 п. 1.5. их пересечение также выпукло.
Определение 1. Область, которая являеться пересечением конечного числа замкнутых полуплоскостей называется замкнутой выпуклой многоугольной областью.
Если замкнутая выпуклая многоугольная область ограничена, то она называется замкнутым выпуклым многоугольником.
В примере №1 п.1.4. это замкнутый выпуклый пятиугольник ОАВСД.
Целевой функции.
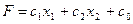 (5)
(5)
соответствует вектор роста 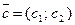 и линии уровня
и линии уровня
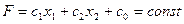 (6)
(6)
На рисунке 1. п 1.4. это линии (А) и (В).
При этом значение функции 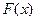 растет в направлении вектора роста
растет в направлении вектора роста 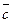 , перпендикулярного линиям уровня.
, перпендикулярного линиям уровня.
Таким образом, геометрически однородная задача ЛП на плоскости может быть сформулирована следующим образом: найти крайнюю (угловую) точку, в которой линия уровня все еще пересекает замкнутую выпуклую многоугольную область при параллельном переносе этой линии в направлении вектора роста (или в противоположном направлении).
В трехмерном пространстве R3 каждому линейному неравенству
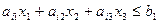 (7)
(7)
Соответствует одно из замкнутых полупространств, на которые делит все пространство R3 плоскость pi , определенная уравнением:
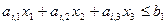 (8)
(8)
Соответственно вектор роста 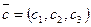 перпендикулярен каждой поверхности уровня целевой функции, задаваемой уравнением:
перпендикулярен каждой поверхности уровня целевой функции, задаваемой уравнением:
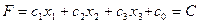 , (9)
, (9)
где С – некая произвольная константа.
Определение 2. Область, которая являеться пересечением конечного числа замкнутых полупространств в R3 называется выпуклой многогранной областью. Ограниченная выпуклая многогранная область называется выпуклым многогранником.
Однородная задача ЛП в пространстве R3 может быть сформулирована так: найти крайнюю (угловую) точку, в которой поверхность уровня при движении в направлении вектора роста (или в противоположном направлении) все еще пересекает заданную выпуклую многогранную область.
Заметим, что при этом поверхность уровня представляет из себя плоскость, определяемую уравнением (9). Вектор роста 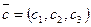 является вектором нормали этой плоскости.
является вектором нормали этой плоскости.
Соответствующая формулировка в n – мерном пространстве Rn фактически совпадает с данной. Единственное отличие состоит в том, что уравнение поверхности уровня:
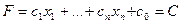 (10)
(10)
задает не плоскость, а гиперплоскость в Rn.
1.8. Симплекс-метод решения задачи линейного программирования.
1.8.1. Пример решения задачи линейного программирования симплекс-методом.
Рассмотрим однородную задачу ЛП из примера №1 п. 1.5.:
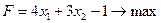
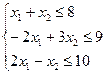 (1)
(1)
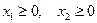
Добавив к левым частям системы неравенств соответствующие балансовые переменные 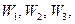 преобразуем задачу (1) в каноническую форму:
преобразуем задачу (1) в каноническую форму:
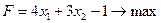
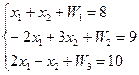 (2)
(2)
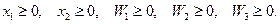
Для удобства и единообразия запишем определение целевой функции  в виде уравнения:
в виде уравнения:
 (3)
(3)
Запишем (2) и (3) в виде первой симплекс таблицы:

| 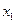
| 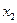
| 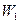
| 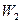
| 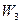
| 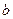
| |
| - 2 | (4) | ||||||
| - 1 | |||||||
| - 4 | - 3 | - 1 |
Первые три строки таблицы (4) содержат по сути расширенную матрицу системы линейных уравнений (2), к которой слева приписан столбец переменной  . Последняя строка, называемая индексной, содержит уравнение (3). Буквой
. Последняя строка, называемая индексной, содержит уравнение (3). Буквой 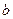 , как обычно, обозначен столбец свободных членов. Отметим, что таким образом составленная таблица (4) называется симплексной, поскольку задача (2) имеет симплексную форму. Напомним, что это означает, что во-первых, матрица системы (и таблица (4)) содержат т базисных столбцов (столбцы
, как обычно, обозначен столбец свободных членов. Отметим, что таким образом составленная таблица (4) называется симплексной, поскольку задача (2) имеет симплексную форму. Напомним, что это означает, что во-первых, матрица системы (и таблица (4)) содержат т базисных столбцов (столбцы 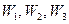 ), где т - число уравнений (в данном случае
), где т - число уравнений (в данном случае 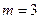 ); во-вторых, все элементы столбца свободных членов неотрицательны (это числа 8, 9 и 10), кроме, возможно, элемента индексной строки; в- третьих, целевая функция
); во-вторых, все элементы столбца свободных членов неотрицательны (это числа 8, 9 и 10), кроме, возможно, элемента индексной строки; в- третьих, целевая функция  зависит только от свободных переменных (
зависит только от свободных переменных ( 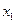 и
и 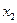 ). Последнее верно, поскольку в базисных столбцах (
). Последнее верно, поскольку в базисных столбцах ( 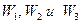 ) в индексной строке находятся только нули. Первая симплекс-таблица (4) определяет первое опорное решение. Напомним, что опорное решение является допустимым базисным решением, и, следовательно, свободные переменные
) в индексной строке находятся только нули. Первая симплекс-таблица (4) определяет первое опорное решение. Напомним, что опорное решение является допустимым базисным решением, и, следовательно, свободные переменные 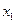 и
и 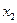 равны нулю:
равны нулю: 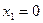 и
и 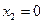 .
.
Далее, переменная 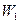 определяется первой строкой таблицы (4), которая является сокращённой записью первого уравнения системы (2). При
определяется первой строкой таблицы (4), которая является сокращённой записью первого уравнения системы (2). При 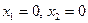 оно принимает вид:
оно принимает вид:
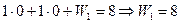
Вторая строка таблицы определяет переменную 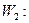
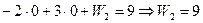
Третья строка определяет 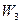 :
: 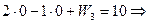
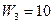
Значение целевой функции определяем по индексной строке: 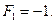
В дальнейшем мы покажем, что оптимальное решение канонической задачи ЛП является опорным, и, следовательно, его следует искать среди опорных решений. Симплекс-таблица (4) и дает одно из таких решений. Как проверить, является ли оно оптимальным? Оказывается, просто. Как мы увидим далее, если коэффициенты 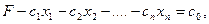 целевой функции
целевой функции  канонической задачи ЛП неположительные:
канонической задачи ЛП неположительные: 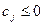 ,- и функция
,- и функция  зависит только от свободных переменных, то соответствующее опорное решение является оптимальным.
зависит только от свободных переменных, то соответствующее опорное решение является оптимальным.
Но условие 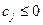 означает, что коэффициенты индексной строки, стоящие в столбцах свободных переменных, должны быть неотрицательны:
означает, что коэффициенты индексной строки, стоящие в столбцах свободных переменных, должны быть неотрицательны: 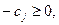 поскольку индексная строка соответствует уравнению:
поскольку индексная строка соответствует уравнению: 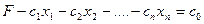 , - и содержит коэффициенты
, - и содержит коэффициенты 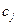 с противоположным знаком.
с противоположным знаком.
Мы видим, что в таблице (4) условие неотрицательности всех элементов индексной строки (разумеется, кроме правой части 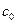 , стоящей в столбце свободных членов) не выполнено. Более того, оба столбца свободных переменных
, стоящей в столбце свободных членов) не выполнено. Более того, оба столбца свободных переменных 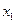 и
и 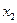 содержат в индексной строке отрицательные элементы: - 4 и -3, - соответственно.
содержат в индексной строке отрицательные элементы: - 4 и -3, - соответственно.
Выберем любой из этих столбцов, например, первый и назовем его ведущим. Определим для каждого 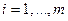 так называемое допустимое отношение
так называемое допустимое отношение 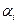 следующим образом. Если в
следующим образом. Если в 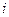 - ой строке ведущего столбца стоит неположительный элемент, то положим
- ой строке ведущего столбца стоит неположительный элемент, то положим 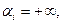 если же этот элемен
если же этот элемен
| <== предыдущая страница | | | следующая страница ==> |
| Говоря о наборе и верстке текста, невозможно не коснуться Microsoft Word - многофункциональной программы обработки текстов | | | Глава II. Транспортная задача |
Дата добавления: 2014-10-14; просмотров: 722; Нарушение авторских прав

Мы поможем в написании ваших работ!