Проекционно-сеточный метод

Основная идея метода заключается в том, что на участках оси независимой переменной τ в качестве решения y принимается функция определенного типа, но с неизвестными пока параметрами (коэффициентами). Выражения для функции и ее производных подставляются в решаемое уравнение. Записывается выражение для функционала S, который представляет собой сумму квадратов невязок (разностей значений правой и левой частей уравнения) для ряда значений независимой переменной. Коэффициенты аппроксимирующей функции находятся путем минимизации функционала S. Можно использовать либо методы безусловной оптимизации, либо прямые методы (что будет рассмотрено далее).

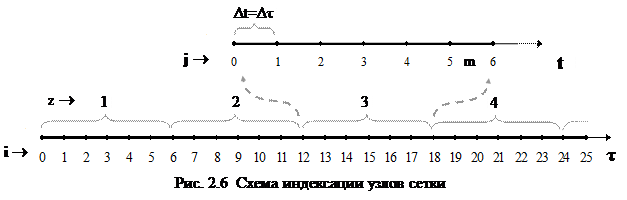
В области определения функции y выделяются узловые точки iс шагом Dt. Назначается последовательность интервалов интегрирования z, каждый из которых включает несколько узловых точек j. В пределах каждого интервала интегрирования используется локальная независимая переменная t.

Решение обыкновенного дифференциального уравнения 1^го порядка:

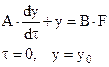(2.23)

где А, В – заданные коэффициенты уравнения, F – воздействие.

В качестве функции аппроксимирующей решение y на каждом интервале интегрирования чаще всего принимается полином kn^ой степени:

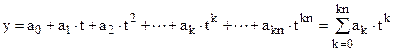(2.24)

Соответственно выражения для производной:

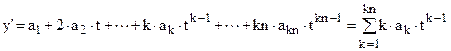(2.25)

где a₁¸a_kn – коэффициенты полинома, подлежащие определению. Значения коэффициента а₀ определяется из удовлетворения начальному условию или решению полученному на предыдущем интервале интегрирования:

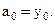(2.26)

Подставляя выражения для y, y¢в решаемое уравнение получим:

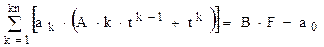(2.27)

Сумма квадратов невязок (разностей значений правой и левой частей уравнения) по всем точкам рассматриваемого интервала интегрирования (j=0¸m) имеет вид:

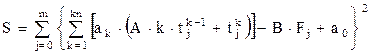(2.28)

Значение функционала S будет минимальным при выполнении условий:

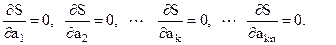(2.29)

Удовлетворяя каждому приведенному условию можно записать СЛАУ имеющую коэффициенты матрицы (МА) и элементы вектора правой части (МВ) определяемые зависимостями:

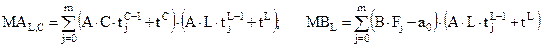(2.30)

где L – индекс строки матрицы (line), C – индекс столбца (column).

В общем случае 1 £ L £ kn, 1 £ C £ kn.

Для дифференциального уравнения первого порядка решение которого аппроксимируется полиномом, порядок матрицы численно равен порядку аппроксимирующего полинома.

Решив полученную СЛАУ найдем значения коэффициентов полинома a₁¸a_kn.

Следует отметить, что при постоянных значениях коэффициентов уравнения A, B и при фиксируемых значениях Δτ и m коэффициенты матрицы MA_L,C одинаковы для всех интервалов интегрирования, а изменяются только значения MB_L.

Рассмотрим конкретный пример аппроксимации решения полиномом третьего порядка.

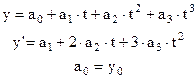(2.31)

Подставим аппроксимирующую функцию и ее производную в решаемое уравнение:

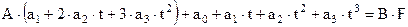
Сумма квадратов невязок для точек интервала Δτ:

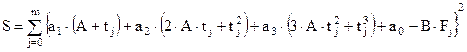
Удовлетворяя условиям:

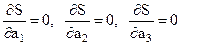
получим СЛАУ третьего порядка.

Рассмотрим первое условие:

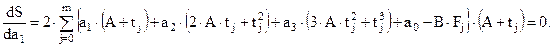
После формальных преобразований получим первое уравнение СЛАУ:

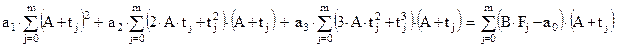
Аналогично получаем второе и третье уравнения:

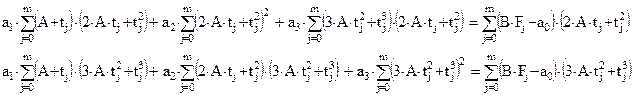
Решение обыкновенного дифференциального уравнения 2^го порядка:

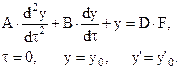(2.32)

где А, В, D – заданные коэффициенты уравнения, F – воздействие.

Выражения для аппроксимирующей функции и ее производных:

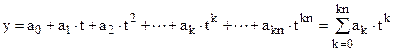
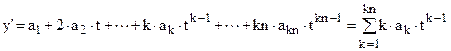
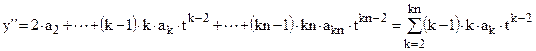
где a₂¸a_kn – коэффициенты полинома, подлежащие определению. Значения коэффициентов а₀ и а₁ определяются из удовлетворения начальным условиям или решению полученному на предыдущем интервале интегрирования:

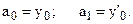
Подставляя выражения для y, y¢ и y¢¢ в решаемое уравнение получим:

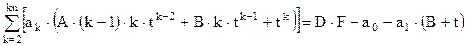
Сумма квадратов невязок для точек рассматриваемого интервала интегрирования (j=0¸m) имеет вид:

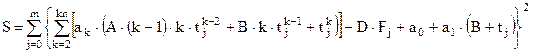
Выполняя условия:

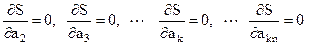
получим выражения для коэффициентов матрицы МА и элементов вектора правой части МВ:

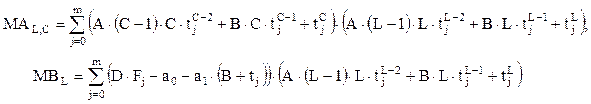
где L – индекс строки матрицы (line), C – индекс столбца (column).

В общем случае 1 £ L £ (kn-1), 1 £ C £ (kn-1).

Для дифференциального уравнения второго порядка, решение которого аппроксимируется полиномом, порядок матрицы на единицу меньше порядка аппроксимирующего полинома.

При постоянных значениях коэффициентов уравнения A, B, D и при фиксируемых значениях Δτ и m коэффициенты матрицы MA_L,C одинаковы для всех интервалов интегрирования, а изменяются только значения MB_L.

Дата добавления: 2014-10-10; просмотров: 407; Нарушение авторских прав

Мы поможем в написании ваших работ!