Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Статистический метод
С помощью этого метода производится оценка вероятности возникновения волн различной высоты. Определить вероятность можно приближенно, взяв довольно длинную запись волнения и сняв с нее высоты волн. Тогда вероятность возникновения волны с амплитудой  , будет равна:
, будет равна:

где 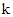 - число волн с амплитудой
- число волн с амплитудой  , на записи; n - общее число волн на записи. Чем длиннее запись, тем более точно определяется вероятность.
, на записи; n - общее число волн на записи. Чем длиннее запись, тем более точно определяется вероятность.
Оценка интенсивности волнения производится с помощью дисперсии (квадрата среднего квадратичного отклонения)
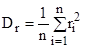
Средняя высота волны (в вероятностном смысле) связана с дисперсией соотношением

На практике обычно применяется не вероятность возникновения волны какой-то высоты, а обеспеченность. Обеспеченность- это вероятность возникновения волн с высотой, большей или равной заданной.
Таким образом, трехпроцентная обеспеченность обозначает, что из 100 волн только 3 будут иметь высоту, большую или равную заданной высоте. Обеспеченность записывается в виде индекса, например  ,
, 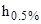 .
.
Средняя высота волны имеет обеспеченность 46,5%, т.е.
 ;
; 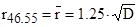
В таблицах балльности волн обычно выписываются значения  , для которых
, для которых
 ;
; 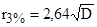 . (2.23)
. (2.23)
Иногда необходимо определить дисперсию волны, зная высоту  Из (2.23) следует
Из (2.23) следует

Высота волны 0,5%-ной обеспеченности называется максимальной и описывается формулой
 ;
;  (2.25)
(2.25)
Обобщенная оценка интенсивности ветрового волнения производится в условных единицах - баллах. В России применяется 9-балльная шкала (табл. 9.1). Связь между средними значениями  , и
, и  в этой таблице определяется по формуле Циммермана.
в этой таблице определяется по формуле Циммермана.
Таблица 9.1 Таблица балльности волнения и ветра
| Балльность волн | Балльность ветра | Длина волн
 , м , м
| Высота волн,  , м , м
| Период волн
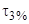 , с , с
| Описательная характеристика |
| 0-1 | Отсутствует | ||||
| I | 2-3 | <5 | 0,25 | <2 | | Слабое |
| II | 3-4 | 5-15 | 0,25-0,75 | 2-3 | Умеренное |
| III | 15-25 | 0,75-1,25 | 3-4 | Значительное | |
| IV | 25-40 | 1,25-2,0 | 4-5 | Значительное | |
| V | 5-6 | 40-75 | 2,0-3,5 | 5-7 | Сильное |
| VI | 6-7 | 75-125 | 3,5-6,0 | 7-9 | Сильное |
| VII | 7-8 | 125-170 | 6,0-8,5 | 9-11 | Очень сильное |
| VIII | 8-9 | 170-220 | 8,5-11,0 | 11-12 | Очень сильное |
| IX | 10-12 | >220 | >11,0 | >12 | Исключительное |
Спектральный метод
Статистический метод не дает всех необходимых данных для описания волнения как непрерывного случайного процесса. Более удобен для этих целей спектральный метод, который основан на представлении реального волнения в виде суммы бесконечного числа единичных волн со случайными амплитудами, частотами и фазами, т.е.
 (2.26)
(2.26)
Погонная энергия каждой отдельно взятой волны в соответствии с (2.19) будет равна:
 .
.
В то же время ее можно представить в виде
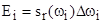
где 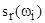 -удельная энергия, приходящаяся на интервал
-удельная энергия, приходящаяся на интервал  при частоте
при частоте 
Приравнивая (2.27) и (2.28), получим
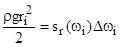
Отсюда
 (2.30),
(2.30),
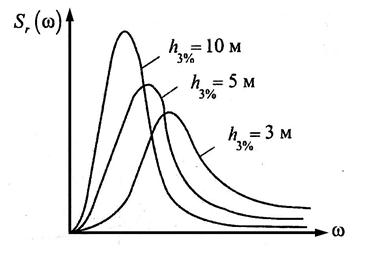
Зависимость  (рис. 2.3) можно представить в виде графика спектральной плотности, или энергетического спектра. Он характеризует распределение энергии волн по амплитудам и частотам.
(рис. 2.3) можно представить в виде графика спектральной плотности, или энергетического спектра. Он характеризует распределение энергии волн по амплитудам и частотам.
|
Рис. 2.3. Спектры нерегулярного волнения различной балльности
Связь между спектральными и статистическими характеристиками можно найтиизвыражения (2.21), подставив в него (2.29):

При 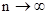
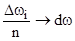 , а сумма становится интегралом.
, а сумма становится интегралом.
Тогда получим

С помощью дисперсии легко установить связь с высотой волны заданной обеспеченности и с соответствующими баллами волнения. Спектры чаще всего представляются в форме
 (2.33)
(2.33)
где А, В, k, п - параметры, зависящие от условий волнообразования, от степени развитости волнения, от балльности, от акватории и т.д.
Обычно спектры нормируют (обезразмеривают), разделив 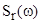 5'г(к>) на D и умножив на среднюю частоту
5'г(к>) на D и умножив на среднюю частоту 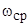 :
:
|
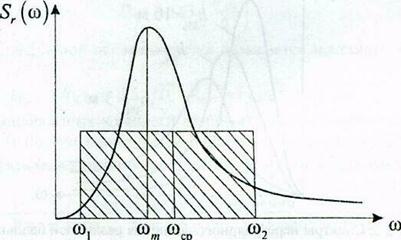
Рис. 9.4. Определение средней частоты спектра

где  - нормированный спектр;
- нормированный спектр;  - безразмерная частота. Удобство нормированных спектров в том, что они не зависят от балльности волнения.
- безразмерная частота. Удобство нормированных спектров в том, что они не зависят от балльности волнения.
Среднюю частоту 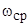 можно определить из выражения
можно определить из выражения
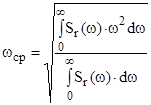 (2.35)
(2.35)
Приближенно 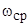 можно определить графически в соответствии с рис. 2.4, при этом
можно определить графически в соответствии с рис. 2.4, при этом

где  и
и  определяются как границы прямоугольника, у которого площадь равна площади под кривой спектральной плотности, а момент инерции площади относительно оси ординат равен моменту инерции площади под кривой.
определяются как границы прямоугольника, у которого площадь равна площади под кривой спектральной плотности, а момент инерции площади относительно оси ординат равен моменту инерции площади под кривой.
Дисперсия при нормировании определяется по формуле (2.24).
Существует статистическая связь между 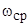 и
и  . Для наиболее употребительных спектров
. Для наиболее употребительных спектров
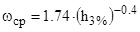 (2.36)
(2.36)
Окончательно в нормированном виде спектральная плотность записывается как
 (2.37)
(2.37)
где  ;
; 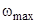 - частота, соответствующая максимуму спектра (см. рис. 2.4);
- частота, соответствующая максимуму спектра (см. рис. 2.4);
 ,
, 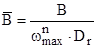
Величина 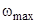 связана с
связана с 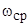 соотношением, зависящим от вида конкретного спектра.
соотношением, зависящим от вида конкретного спектра.
| <== предыдущая страница | | | следующая страница ==> |
| КАЧКА СУДНА | | | Капитальный ремонт щебеночных (гравийных), асфальтобетонных и цементобетонных покрытий |
Дата добавления: 2014-07-11; просмотров: 445; Нарушение авторских прав

Мы поможем в написании ваших работ!