Оценка погрешности разностных схем

Для оценки погрешности метода возникающей при использовании разностных схем проводилось сравнение аналитического и численных решений модельного уравнения. В качестве модельного уравнения выбрано обыкновенное однородное дифференциальное уравнение с постоянными коэффициентами (2.15), описывающее переход объекта из возмущенного состояния в положение статического равновесия.

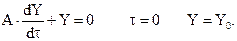(2.15)

где А – коэффициент отражающий свойства объекта;

t – независимая переменная.

Сравнивались решения для значения τ=Δτ. Расчет относительной погрешности решения модельного уравнения (2.15) проводился по зависимости:

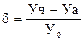(2.16)

где Yч – численное решение модельного уравнения;

Yа – аналитическое решение модельного уравнения;

Y₀ – начальное значение параметра отражающего состояние объекта.

Решения модельного уравнения.

1. Аналитическое:

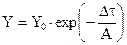(2.17)

2. Явная разностная схема:

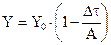условие устойчивости 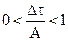(2.18)

3. Неявная разностная схема:

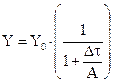условие устойчивости 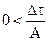(2.19)

4. Схема трапеций:

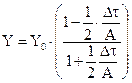условие устойчивости 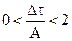(2.20)

5. Схема Рунге-Кутта 4го порядка:

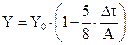условие устойчивости 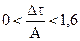(2.21)

6. Аналитико-разностные схемы:

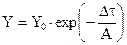условие устойчивости 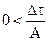(2.22)

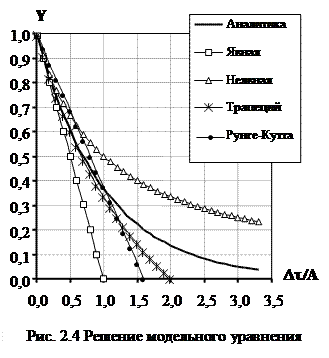
На рис.2.4 приведены графики решения модельного уравнения (2.15) с использованием различных разностных схем кроме экспоненциальных. Решение по экспоненциальным схемам совпадает с аналитическим.

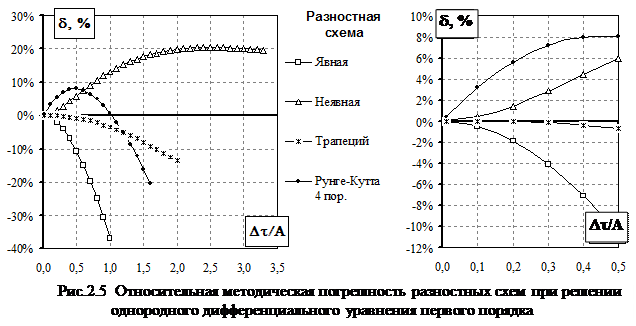
На рис.2.5 показано изменение погрешности численного решения модельного уравнения.

Приведенные графики позволяют в первом приближении оценить возможную погрешность численного решения и выбрать разностную схему.

При выборе разностной схемы объязательно необходимо проводить оценку устойчивости схемы (явная, трапеций, Рунге-Кутта).

Дата добавления: 2014-10-10; просмотров: 356; Нарушение авторских прав

Мы поможем в написании ваших работ!