Виды погрешности обработки

Погрешность обработки- это отклонение полученного при обработке значения геометрического или другого параметра от идеальных.

Погрешности могут также возникнуть также в процессе эксплуатации и хранении машин под воздействием внешней среды, внутренних изменений в структуре материала, износа и т.д.

Погрешность изготовления для совокупности деталей, составляющих обрабатываемую партию, можно разделить на группы:

1.систематические постоянные погрешности, имеющие одинаковые числовые значения для всей рассматриваемой совокупности, вызванные воздействием факторов, сохраняющих постоянное значение в процессе обработки партии (например, погрешности из-за неправильной настройки станка);

2.систематические переменные погрешности, закономерно изменяющихся по ходу технологического процесса (например, погрешности вызванные износом инструмента или температурными деформациями системы СПИД, являющиеся функцией от времени обработки);

3.случайные погрешности или погрешности рассеяния, имеющие для отдельных деталей партии различные значения. Определить заранее момент появления того или иного значения случайной погрешности не представляется возможным. Случайные погрешности вызываются действием факторов, подверженных колебаниям случайного характера, или же действием большого числа факторов, в том числе и систематических, если их вступление в процесс и выключение из него носят случайный характер. Если систематические погрешности могут быть выявлены и в ряде случаев устранены в процессе подготовки производства, то выявление случайных погрешностей требует специального изучения средств и условий изготовления деталей на основе математической статистики, а полностью их исключение не возможно. Случайные погрешности для совокупности деталей можно описать с помощью нормального распределения.

Центр группирования или среднее арифметическое значение рассматриваемого параметра совокупности деталей (диаметр вала):

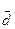=(d_д1+d_д2+···+d_дn)/n…………………………….(1)

где: d_д1+d_д2- действительные размеры деталей;

n- число деталей.

Среднее квадратическое отклонение случайного значения параметра от центра группирования, характеризующее рассеяние или разброс отклонений x_i

σ =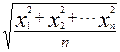 (2)

где: x₁= d_д1-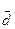; x₂= d_д2-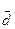; x_i= d_дn-.

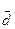Закон распределения случайной погрешности в виде уравнения и соответствующей кривой устанавливает зависимость между значением случайной погрешности и вероятностью ее появления.

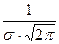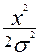y= exp- (3)

Вероятность получения случайной погрешности со значениями, лежащими в пределах от x₁ до x₂, определяется площадью, заключенной между кривой плотности вероятности, осью абсцисс и ординатами точек x₁ и x₂.

Нормальное распределение играет особую роль в теории вероятностей и математической статистике. Разнообразные статистические данные с хорошей степенью точности можно считать реализациями случайной величины, имеющей нормальное распределение. Можно предполагать нормальное распределение у случайной величины, если на ее отклонение от некоторого заданного значения влияет множество различных факторов, причем влияние каждого из них вносит малый вклад в это отклонение, а их действия почти независимы. Кроме того, в силу центральной предельной теоремы распределение целого ряда широко распространенных в статистике функций от случайных величин хорошо аппроксимируется нормальным распределением. Нормальное распределение часто встречается в реальных исследованиях. Оно удобно для компьютерной обработки. Использованию нормального распределения для приближенного описания случайных величин не препятствует то обстоятельство, что эти величины обычно могут принимать значения только из какого-то ограниченного интервала (скажем, размер изделия должен быть больше нуля и меньше километра), а нормальное распределение не сосредоточено целиком ни на каком интервале. Однако, вероятность больших отклонений нормальной случайной величины от среднего значения настолько мала, что ее практически можно считать равной нулю. Кроме того, линейная комбинация любых нормально распределённых величин вновь распределена нормально.

Для исследования "нормальных" данных математической статистикой выработаны эффективные методы. Эти методы непригодны для данных другой природы в том смысле, что выполнить соответствующий расчёт можно, но результат будет неправильным. Поэтому, когда к имеющимся наблюдениям применяются ориентированные на нормальное распределение методы, необходимо выяснить, похоже ли распределение этих наблюдений на нормальное. С полной уверенностью сказать это невозможно, но, по крайней мере, от грубых ошибок такие проверки могут уберечь.

Случайная величина ξ имеет нормальное распределение вероятностей с параметрами а и σ² (краткое обозначение: ξ ~ N(a, σ²)), если ее плотность распределения задается формулой:

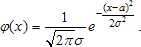
Математическое ожидание и дисперсия случайной величины ξ ~ N(a, σ²) равны: Е(ξ) = a, D(ξ) = σ²;
Асимметрия равна нулю. Эксцесс (четвертый центральный момент, отнесённый к квадрату дисперсии за вычетом 3) равен нулю. Случайная величина группируется вблизи a, причем типичные отклонения от a близки к σ (σ > 0). Плотность распределения стремится к нулю при удалении х от среднего значения. График функции плотности симметричен относительно точки а. Значит, медиана нормального распределения равна а. В точке а функция φ(х) достигает своего максимума, который равен . Значит, мода нормального распределения равна а. Таким образом, параметр а характеризует положение графика функции на числовой оси. Это параметр положения. Параметр характеризует степень сжатия или растяжения графика плотности. Это параметр масштаба. Вся совокупность нормальных распределений представляет собой двухпараметрическое семейство.

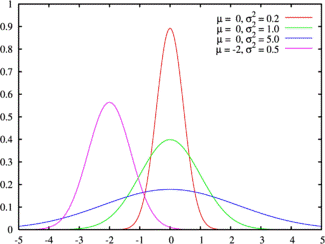Зеленая линия соответствует стандартному нормальному распределению

Вывод:

Заключение:

Дата добавления: 2014-03-13; просмотров: 1177; Нарушение авторских прав

Мы поможем в написании ваших работ!