Схемы на основе аналитического решения (аналитико-разностные схемы)

Одним из способов построения разностных схем является использование точного аналитического решения на интервале интегрирования равного шагу сетки. В пределах интервала интегрирования используется новая координатная ось t как показано на рис. 3 и проводится решение уравнения 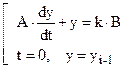(2.9):

(2.9)

В зависимости от способа представления B возможны варианты организации схем.

Схема при постоянном воздействии (схема B=const).

При В=const аналитическое решение (2.9) имеет вид:

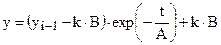
где В - принятое на интервале интегрирования постоянное значение воздействия. Разумно принять: 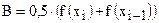. Тогда:

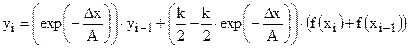(2.10)

Рассмотренная схема абсолютно устойчива, поскольку всегда выполняется условие:

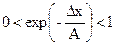(2.11)

Схема при линейном воздействии (схема B=a+b×t).

При линейной зависимости B=a+b×t аналитическое решение (2.9) имеет вид:

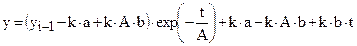(2.12)

С учетом того, что на интервале интегрирования принято линейное изменение величины В от f(x_i-1) до f(x_i) в нашем случае:

.

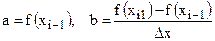Разностная схема принимает вид:

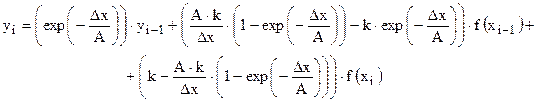(2.13)

Рассмотренная схема абсолютно устойчива, поскольку всегда выполняется условие (2.11).

Схема Рунге-Кутта четвертого порядка (решение уравнения 2.2).

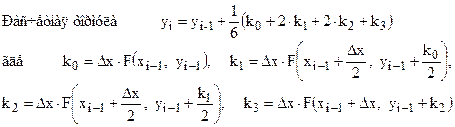(2.14)

Дата добавления: 2014-10-10; просмотров: 327; Нарушение авторских прав

Мы поможем в написании ваших работ!