Введение в компьютерное моделирование

Задача о передаче теплоты через цилиндрическую стенку трубы очень часто встречается в практике. Этот класс задач также относится к одномерному случаю, если распространение тепловой энергии рассматривать в цилиндрических координатах. В случае, когда заданы постоянные температуры на внутренней и наружной стенках трубы, то изменение температуры происходит только вдоль радиуса (рис. 10.6).

Рис. 18.6. Теплопроводность через цилиндрическую стенку

Согласно закону Фурье количество теплоты, передаваемой через стенку, определяется следующим образом:

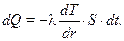(10.18)

С учетом того, что площадь боковой поверхности цилиндра 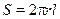, выражение (10.18) принимает вид

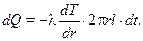(10.19)

Заметим, что для цилиндрической стенки неприемлема такая характеристика, как удельный тепловой поток. Это объясняется тем, что с ростом радиуса увеличивается и площадь боковой поверхности S поэтому удельный тепловой поток 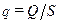не остается постоянным в каждом сечении, как для плоской стенки, а уменьшается с ростом радиуса. Поэтому для цилиндрических поверхностей вводится новая характеристика — погонный тепловой поток.

Погонным тепловым потоком q_l называется количество теплоты, передаваемой через цилиндрическую поверхность единичной длины в единицу времени.

С учетом выражения (10.19), получим

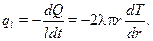(10.20)

Разделим переменные в выражении (10.20)

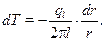(10.21)

После интегрирования выражения (10.21) получаем

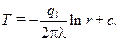(10.22)

Согласно граничным условиям при 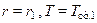, т.е.

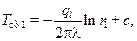(10.23)

а при 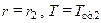, т. е.

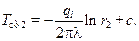(10.24)

Вычтем из выражения (10.23) выражение (10.24) и получим

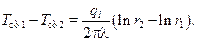
После несложных преобразований из (10.25) окончательно по­лучаем

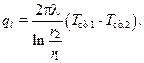(10.26)

С учетом (10.26) из выраження (10.23) легко определяется по­стоянная интегрирования

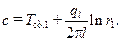(10.27)

Подставим выражение (10.27) в (10.22) и после несложных преобразований получим

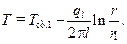(10.28)

Как видно из выражения (10.28), температура по толщине цилиндрической стенки изменяется по логарифми-ческому закону.

Если в выражении (10.26) ввести понятие термического сопротивления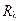

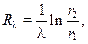
то получим следующую запись для погонного теплового потока

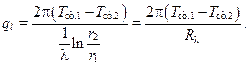(10.29)

Для определения погонного теплового потока через многослойную цилиндрическую стенку надо просуммировать термические сопротивления отдельных слоев

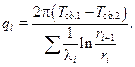(10.30)

В заключение заметим, что тепловые расчеты для цилиндрической стенки по формулам (10.26), (10.29), (10.30) целесообразно вести только при существенном отличии наружного и внутреннего радиусов цилиндра, т. е. при выполнении условия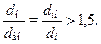

В противном случае целесообразно воспользоваться зависимостями для плоской стенки.

Кроме того, во всех приведенных формулах для тепловых потоков температура может подставляться как в Кельвинах, так и в градусах Цельсия, так как в этом случае определяется разность температур.

Введение в компьютерное моделирование

В последние годы все чаще говорят о компьютерных экспериментах и необходимых для их проведения компьютерных инструментах.

Компьютерные эксперименты отличаются от привычных натурных экспериментов тем, что исследователь экспериментирует не с реальным объектом, а с его компьютерной моделью.

Компьютерное моделирование как метод исследования является естественным развитием математического моделирования. В основе компьютерных моделей, по крайней мере тех, о которых речь пойдет далее, лежат математические модели. Эти модели строятся автоматически по описанию структуры и поведения исследуемой системы, принятому в языке моделирования. Построенные математические модели обычно сводятся к системам уравнений, решение которых редко удается найти в замкнутой форме, и их приходится решать численно, с помощью программных реализаций численных методов. Программная реализация математической модели строится автоматически пакетом моделирования. Наконец при компьютерном моделировании широко используется возможность визуализации как самой модели, так и ее поведения.

Исследуемая модель предстает перед пользователем в виде узнаваемых графических образов, ее параметры можно регулировать и ею можно управлять почти так же, как и в реальной жизни. В компьютерной модели используемая математическая модель, ее программная реализация, системное и математическое программное обеспечение, необходимые для воспроизведения поведения модели, спрятаны за дружественным интерфейсом. Все это позволяет создавать и исследовать компьютерные модели специалистам, далеким от прикладной математики и информатики.

Для разработки компьютерных моделей и экспериментирования с ними создано специальное программное обеспечение— универсальные среды моделирования, которые уже практически повсеместно вытеснили ручное исследование сложных математических моделей. Эти инструменты, включающие графические редакторы моделей и виртуальные стенды, постепенно заменяют особый вид программного обеспечения — пакеты прикладных программ, еще недавно использовавшиеся для проведения вычислительного эксперимента. Системы моделирования позволяют создавать виртуальные, или лучше компьютерные, лаборатории, аналогичные реальным, оснащенные моделями измерительных приборов и датчиками сигналов.

Современные инструменты моделирования предлагают исследователям новые технологии математического моделирования и проведения вычислительного эксперимента.

Нашей целью является изучение методов построения компьютерных моделей, возможностей компьютерного моделирования и технологий проведения компьютерных экспериментов.

Будем рассматривать только модели, в основе которых лежат динамические и гибридные системы. Такие математические модели назовем сложными динамическими системами.

Модель

Зарождение любой естественной науки начинается с натурных экспериментов над реальными объектами и системами для выяснения их свойств, обнаружения закономерностей и законов, которым они подчиняются. Однако давно было замечено, что очень много можно узнать о реальном мире, если вместо реальных объектов изучать их упрощенные заменители— модели. В последующем выяснилось, что строить и использовать модели можно не только для познания окружающего нас мира.

Дата добавления: 2014-08-04; просмотров: 501; Нарушение авторских прав

Мы поможем в написании ваших работ!