Теплопроводность через цилиндрическую стенку

Задача о передаче теплоты через цилиндрическую стенку трубы очень часто встречается в практике. Этот класс задач также относится к одномерному случаю, если распространение тепловой энергии рассматривать в цилиндрических координатах. В случае, когда заданы постоянные температуры на внутренней и наружной стенках трубы, то изменение температуры происходит только вдоль радиуса (рис. 10.6).

Рис. 18.6. Теплопроводность через цилиндрическую стенку

Согласно закону Фурье количество теплоты, передаваемой через стенку, определяется следующим образом:

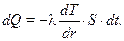(10.18)

С учетом того, что площадь боковой поверхности цилиндра 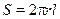, выражение (10.18) принимает вид

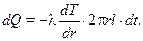(10.19)

Заметим, что для цилиндрической стенки неприемлема такая характеристика, как удельный тепловой поток. Это объясняется тем, что с ростом радиуса увеличивается и площадь боковой поверхности S поэтому удельный тепловой поток 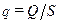не остается постоянным в каждом сечении, как для плоской стенки, а уменьшается с ростом радиуса. Поэтому для цилиндрических поверхностей вводится новая характеристика — погонный тепловой поток.

Погонным тепловым потоком q_l называется количество теплоты, передаваемой через цилиндрическую поверхность единичной длины в единицу времени.

С учетом выражения (10.19), получим

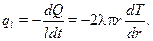(10.20)

Разделим переменные в выражении (10.20)

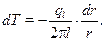(10.21)

После интегрирования выражения (10.21) получаем

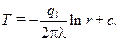(10.22)

Согласно граничным условиям при 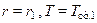, т.е.

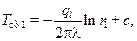(10.23)

а при 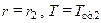, т. е.

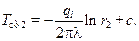(10.24)

Вычтем из выражения (10.23) выражение (10.24) и получим

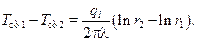
После несложных преобразований из (10.25) окончательно по­лучаем

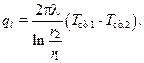(10.26)

С учетом (10.26) из выраження (10.23) легко определяется по­стоянная интегрирования

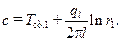(10.27)

Подставим выражение (10.27) в (10.22) и после несложных преобразований получим

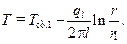(10.28)

Как видно из выражения (10.28), температура по толщине цилиндрической стенки изменяется по логарифми-ческому закону.

Если в выражении (10.26) ввести понятие термического сопротивления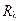

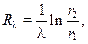
то получим следующую запись для погонного теплового потока

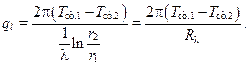(10.29)

Для определения погонного теплового потока через многослойную цилиндрическую стенку надо просуммировать термические сопротивления отдельных слоев

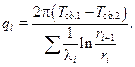(10.30)

В заключение заметим, что тепловые расчеты для цилиндрической стенки по формулам (10.26), (10.29), (10.30) целесообразно вести только при существенном отличии наружного и внутреннего радиусов цилиндра, т. е. при выполнении условия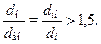

В противном случае целесообразно воспользоваться зависимостями для плоской стенки.

Кроме того, во всех приведенных формулах для тепловых потоков температура может подставляться как в Кельвинах, так и в градусах Цельсия, так как в этом случае определяется разность температур.

Дата добавления: 2014-08-04; просмотров: 925; Нарушение авторских прав

Мы поможем в написании ваших работ!