Лекция 19. Теплопроводность плоских и цилиндрических стенок

Для полного использования внутренней энергии газа необходимо за соплом получить сверхзвуковую скорость. Однако в суживающихся соплах удельный объем газа v₂, достигнув критического значения v_кр, не может больше увеличиваться из-за суживающегося профиля сопла. Поэтому скорость истечения газа с₂ может быть меньше или равна скорости звука. Для того чтобы за соплом получить сверхзвуковую скорость, нужно иметь за ним давление меньше критического. Это достигается только применением комбинированного сопла, называемого соплом Лаваля по имени ученого, впервые применившего такое сопло для получения высоких скоростей газа.

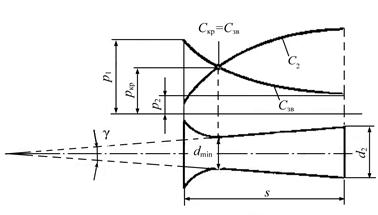
На рис. 12.5 представлена схема сопла Лаваля и график изменения давления газа и скорости его истечения. Комбинированное сопло состоит из двух частей. Первая часть — суживающаяся (до диаметра d_мин с площадью сечения А_мин)работает как дозвуковое сопло, вторая часть — расширяющаяся (до диаметра d₂ с площадью сечения А₂) — как сверхзвуковое.

Из курса физики известно, что скорость звука в газовой среде с параметрами р и v равна 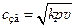, где k — показатель адиабаты. Для идеальных газов pv = RT, поэтому скорость звука

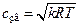
Из последней формулы видно, что скорость звука находится в прямой зависимости от температуры среды.

Протекая по второй части сопла, газ адиабатно расширяется. При этом его давление и температура падают, а скорость истечения возрастает. Однако в первой части сопла она не достигает скорости звука в среде, несмотря на то, что скорость звука с понижением температуры среды падает. В горловине сверхзвукового сопла, т. е. в наименьшем сечении сопла площадью A_мин, устанавливаются критическое давление Р_кр газа и критическая скорость с_кр, равная скорости звука в среде.

Рис. 12.5. Схема сопла Лаваля и график изменения давления газа и скорости его истечения

При движении по расширяющейся части сопла происходит дальнейшее расширение газа. Возрастают его скорость и удельный объем, а давление понижается. Понижается и скорость звука в среде. На выходе из сопла давление становится равным давлению среды, в которую газ вытекает, а скорость истечения газа становится больше скорости звука в среде: с_газа>с_зв.

Применение расширяющегося сопла позволило увеличить скорость истечения за счет более полного использования перепада давлений. При этом массовый расход m_макс остается постоянным, так как расход газа через сопло определяется минимальным сечением сопла площадью A_мин и критическими параметрами с_кр и v_кp, которые не зависят от расширяющейся части сопла.

Увеличить массовый расход вытекающего газа через сопло Лаваля можно, повысив начальное давление и увеличив минимальное сечение площадью А_мин сопла. Максимальный массовый расход газа m_макс определяется по формуле (12.16).

Суживающаяся часть сопла Лаваля выполняется, как обычное суживающееся сопло. Расширяющаяся часть выполняется с углом конусности γ = 10 — 12°. При больших углах конусности возможен отрыв струи от стенок сопла, что резко увеличивает необратимые потери. Длина расширяющейся части сопла s определяется углом конусности γ и величинами A₂ и А_мин.

Если допустить, что расширяющаяся часть комбинированного сопла выполнена с прямолинейными образующими и с углом конусности γ, то длина этой части сопла (см. рис. 12.5) будет равна

s = (d₂ – d_мин)/2tg(γ/2),

где d₂ – d_мин — диаметры выходного и минимального сечений сопла.

Коэффициент скорости. До сих пор истечение рассматривалось в предположении адиабатного расширения газа без трения его о стенки сопла. В действительных условиях процесс истечения всегда происходит с некоторыми потерями энергии газа на совершение неизбежной работы трения. Поэтому действительная скорость истечения с_д всегда меньше теоретической скорости с₂, определяемой по формулам, приведенным в настоящей главе. Отношение с₁/с₂ = φ называют коэффициентом скорости, который всегда меньше единицы. По данным опытов, в зависимости от плавности переходов сечений и качества обработки внутренней поверхности сопла коэффициент φ = 0,93—0,98. В среднем можно принимать φ = 0,95.

Лекция 19. Теплопроводность плоских и цилиндрических стенок.

19. 1. Теплопроводность через плоскую стенку.

Простым примером задач теплопроводности является задача о теплопередаче через плоскую стенку, плоский слой жидкости или газа.

В качестве примера рассмотрим здесь только плоскую стенку (рис. 10.4) толщиной 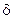, выполненную из однородного материала 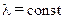. На поверхностях стенки поддерживаются постоянные температуры. При этом теплота передается слева направо. В этом случае имеет место изменение температуры только вдоль оси х, которая направлена, как показано на рис. 10.4.

Таким образом, здесь рассматривается одномерная задача. Граничные условия для этой задачи: на левой поверхности при 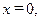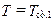, на правой поверхности при .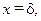

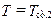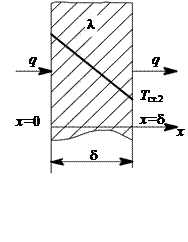
Рис. 10.4. Теплопроводность через плоскую стенку

Рассмотрим стационарную задачу, для которой согласно определению 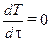(т. е. 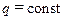). Из выражения (10.6) следует 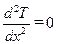. Проинтегрировав это выражение, получим

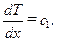(10.8)

Проинтегрировав выражение (10.8), окончательно получаем

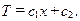(10.9)

Определим постоянные интегрирования с₁ и с₂. Для граничного условия при x=0 из (10.9) следует

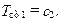(10.10)

Для граничного условия при 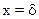с учетом (10.10) из (10.9) следует

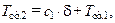
откуда видно, что

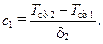(10.11)

Окончательно, подставив выражения (10.10) и (10.11) (с учетом того, что 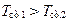) в выражение (10.9), получаем закон изменения температуры по толщине стенки:

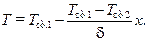(10.12)

Как видно из выражения (10.12), это изменение носит линейный характер.

Определим удельный тепловой поток, проходящий через стенку, для чего воспользуемся законом Фурье (10.2). Причем в этом выражении 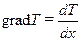. Определив первую производную по x в выражении (10.12), окончательно имеем

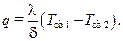(10.13)

Величину 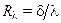в выражении (10.13) часто называют тепловым сопротивлением. С учетом 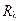выражение (10.13) напоминает хорошо известный закон Ома для участка цепи

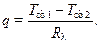
Рассмотрим теплообмен через плоскую многослойную стенку (рис. 10.5).

Поскольку рассматривается стационарная задача, то тепловой поток в каждом слое есть величина постоянная:

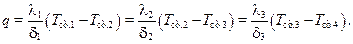(10.14)

Выражение (10.14) можно преобразовать к следующему виду:

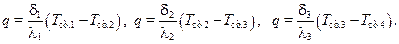(10.15)

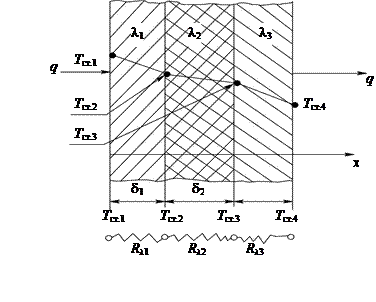Рис. 10.5. Теплопроводность через плоскую многослойную стенку

Сложим левые и правые части выражения (10.15) и получим

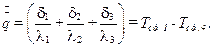(10.16)

Из выражения (10.16) легко получить формулу, справедливую для n-слойной пластины

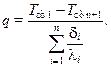(10.17)

Как видно из (10.17), и здесь можно провести аналогию с законом Ома для участка цепи с последовательно включенными сопротивлениями.

Дата добавления: 2014-08-04; просмотров: 652; Нарушение авторских прав

Мы поможем в написании ваших работ!