
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Выражение деформаций через перемещения
Выделим малую частицу упругого тела, т. е. элемент объемом dxdydz в ближайшей окрестности некоторой точки O (рис. 5.2).
 |
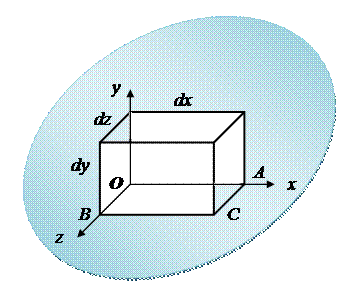 |
Рис. 5.2
Рассмотрим деформацию элемента (ограниченное штриховой линией), а осевые перемещения u, v, w являются составляющими полного перемещения точки O относительно осей координат.
а) Линейные деформации. Вдоль оси x перемещение ребра ОA, будет 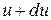 следовательно,
следовательно,
абсолютное удлинение duребра OA, равно
 или
или 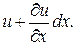
Относительные деформации удлинения -ε, сдвига –γ. Для указания направления деформирования используем те же индексы, что и для составляющих напряжений. Например, относительное удлинение (деформация)частицы элемента в точке O в направлении оси x определится отношением:
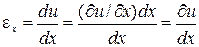 .
.
Аналогично относительные удлинения по направлению осей y и z задаются производными
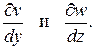
В результате получим три соотношения
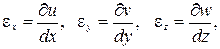 (5.2)
(5.2)
выражающие линейную относительную.деформацию (εx, εy, εz) через одно соответствующее перемещение (u, v или w).
Б)Сдвиговые деформации. Рассмотрим изменение угла между отрезками OA и OB (рис. 5.3), которые до деформирования тела были взаимно перпендикулярны. Отложим на рисунке величины u и v – перемещения точки O в направлении осей x→и и y→v. Перемещения точки A в направлении оси y и точки B в направле нии оси x будут соответственно равны
нии оси x будут соответственно равны
 |
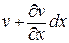 и
и 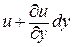 .
.
Рис. 5.3
За счет этих перемещений направление отрезка O1A1 О׀В׀ угол
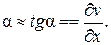
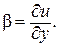
Поэтому первоначальный прямой угол AOB между отрезками OA и OB уменьшится на величину
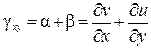 . (а)
. (а)
Эта величина представляет собой относительную деформацию сдвига в плоскости xy (см. рис. 5.3).
Аналогичным образом можно найти деформацию сдвига элементарной частицы в плоскостях yz и xz (см. рис.5.2):
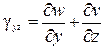 ,
, 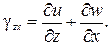 (б)
(б)
Шесть величин, определяемых формулами (5.2), (а) и (б),
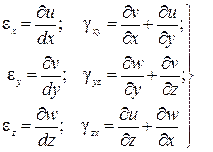 (5.3)
(5.3)
 называются формулами (или соотношениями) Коши*.
называются формулами (или соотношениями) Коши*.
| <== предыдущая страница | | | следующая страница ==> |
| Перемещения и деформации | | | Тензор деформаций |
Дата добавления: 2014-03-03; просмотров: 711; Нарушение авторских прав

Мы поможем в написании ваших работ!