Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Тензор деформаций
Формулы (5.3) выражают деформации в некоторой точке O элемента через относительные деформации (линейные ε и угловые γ).
| Деформированным состояниемвближайшейокрестностинекоторой точки О упругого элемента, называют такое состояние бесконечно малой частицы элемента, которое определяется совокупностью всех векторов деформаций, действующих на данной площадке. |
Совокупность девяти величин
,
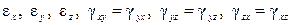определяет тензор деформации.
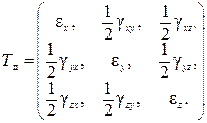(5.5)
тензор деформации (Tд) полностью определяет деформированное состояние в заданной точке упругого элемента.
Взаимная перестановка индексов при угловых деформациях не меняет смысла обозначаемых величин. Поэтому тензор деформаций (5.5) обладает симметрией относительно главной диагонали, на которой расположены линейные деформации, как и тензор напряжений (3.3). Отличие лишь в том, что переход от угловых деформаций к соответствующим компонентам тензора деформаций происходит путем умножения на коэффициент ½, что связано с особенностями тензорного исчисления.
Величину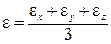 
(5.5)
называют средней деформацией в точке. С ее помощью тензор деформаций (5.5) можно представить в виде суммы шарого и девиаторного тензоров деформаций: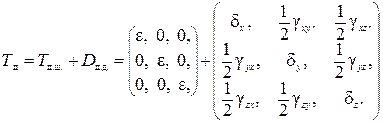 
(5.6)
Шаровой тензор Tд.ш.характеризуется значениями удлинений
εx=εy=εz=ε
и отсутствием сдвигов γxy=γyz=γzx=0.
Шаровой тензор деформаций определяет объемную деформацию частицы упругого элемента.
Девиаторный тензор Dд. определяется величинами
δx=εx–ε; δy=εy–ε; δz=εz–ε; ½γxy; ½γxy; ½γxy,
отражающими геометрию деформации сдвига.
Представление (5.6) удобно в связи с различием в поведении материала при его объемном расширении (или сжимаемости) и при сдвиге. Шесть функций εx; εy; εz; γxy; γxy; γxy, зависящих от координат (x, y и z), определяют деформированное состояние всего тела.
| Если функции не зависят от координат, то деформацию тела называют однородной, в противном случае – неоднородной. |
| <== предыдущая страница | | | следующая страница ==> |
| Выражение деформаций через перемещения | | | Деформаций и напряжений |
Дата добавления: 2014-03-03; просмотров: 723; Нарушение авторских прав
Мы поможем в написании ваших работ!