Диаграмма Мора для деформаций

Рассмотренная аналогия позволяет построить круг Мора для деформаций. (рис. 5.2). При этом линейные деформации откладываются по горизонтальной оси, а угловые деформации 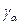делятся пополам и откладываются по вертикальной оси. Центр круга C имеет абсциссу, равную 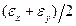; точка B имеет координаты 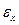и 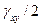. Точка Г, диаметрально противоположная точке B, представляется деформациями, отнесенные к осям, повернутым на угол .

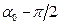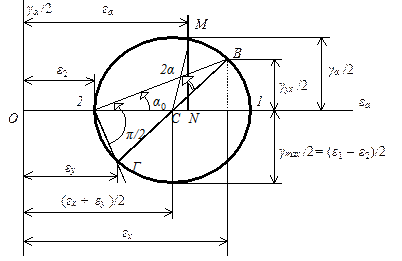
Рис.5.2 Круговая диаграмма плоской деформации.

Деформации, отнесенные к осям, определяемым произвольным углом α, задаются точкой М, положение которой определяется углом 2α, отсчитываемым от точки В. Главные деформации ε₁ и ε₂ на круге деформаций задаются положением точек 1 и 2 соответственно. Наибольшим деформациям сдвига отвечают самая верхняя и самая нижняя точки круга деформаций. Для случая плоской деформации, сохраняется и при рассмотрении трехмерной (объемной) задачи. Полная диаграмма деформаций представляется тремя кругами (рис. 5.3), в которых, для удобства построения, принято условие, что ε₁ > ε₂ > ε₁ > 0.

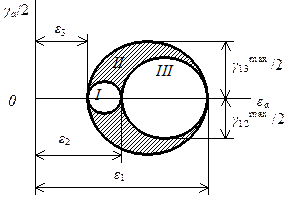
Рис. 5.3. Полная диаграмма деформаций

Из рисунка непосредственно следует, что для главных деформаций справедливы равенства: , , ,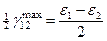

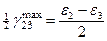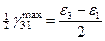или , , 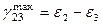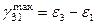. (5.19)

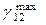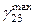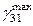Здесь: — сдвиг между направлениями биссектрис двух прямых углов, образованных направлениями главных деформаций ε₁ и ε₂; и — определяются аналогично. Наибольшие деформаци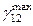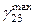и , и 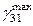часто называют главными сдвигами. Относительные линейные деформации вдоль направлений, между которыми происходят максимальные сдвиги (11.15), равны полу сумме соответствующих главных деформаций:

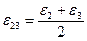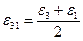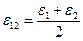, , . (5.20)

Дата добавления: 2014-03-03; просмотров: 1076; Нарушение авторских прав

Мы поможем в написании ваших работ!