
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Объемная деформация
|
Читайте также: |
 Если, до деформации твердого тела, длины ребер элементарной частицы (рис.5.1) соответственно равны dx, dy и dz, то исходный объем этой частицы будет равен dV = dxdydz.
Если, до деформации твердого тела, длины ребер элементарной частицы (рис.5.1) соответственно равны dx, dy и dz, то исходный объем этой частицы будет равен dV = dxdydz.
При деформировании упругого тела изменятся длины ребер частицы, и ее объем станет равным:
d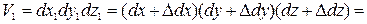
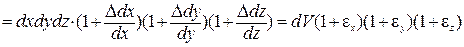 . (a)
. (a)
Перемножив выражения в скобках, получим
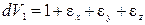
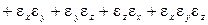 . (b)
. (b)
В теории малых деформаций считается, что величины относительных удлинений εx, εy, εz не превышают величины 0,05. Поэтому их произведениями в (b) можно пренебречь. Пренебрегают также и изменениями объема, вызываемыми деформациями сдвига. Поэтому объемная относительная деформация,равная отношению приращения объема к его исходно величине, будет равна
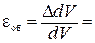
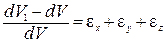 (5.17)
(5.17)
или, с учетом соотношений Коши (2.3),
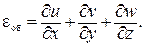 (5.18)
(5.18)
| Объемная деформация равна алгебраической сумме линейных деформаций. |
Пренебрегают также и изменениями объема, вызываемыми деформациями сдвига. Поэтому объемная относительная деформация,равная отношению приращения объема к его исходной величине,
Таким образом, относительная объемная деформация равна алгебраической сумме относительных линейных деформаций. В такой формули ровке выражения (5.17) и (5.18) справедливы как для упругих, так и для упругопластических деформаций.
ровке выражения (5.17) и (5.18) справедливы как для упругих, так и для упругопластических деформаций.
| <== предыдущая страница | | | следующая страница ==> |
| Деформированного состояния | | | Диаграмма Мора для деформаций |
Дата добавления: 2014-03-03; просмотров: 856; Нарушение авторских прав

Мы поможем в написании ваших работ!