Студопедия

Главная страница Случайная лекция


Мы поможем в написании ваших работ!

Порталы:

БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика



Мы поможем в написании ваших работ!




Выражение условия совместности деформаций через напряжения

Читайте также:
  1. D. 17.1.22.11). - Maндатарий может отказаться от договора так, чтобы за мандан­том осталось ненарушенным право с удобством устроить то же дело лично или через другого мандатария.
  2. D. 20.1.1). - Завещание есть правомерное выражение воли, сделанное торжественно для того, чтобы оно действовало после нашей смерти.
  3. Hарушение условия кругового ожидания
  4. I 4. Условия эффективности педагогической оценки
  5. III. Безопасность в условиях технологичных чрезвычайных ситуаций (ТЧС).
  6. VI. Условия для игры.
  7. Автоматическое регулирование напряжения трансформаторами с РПН
  8. Алгоритм расчета теплопередачи через непроницаемые стенки
  9. Анализ инвестиционных проектов в условиях инфляции
  10. Астрономическая, когда наблюдаемый объект находится на бесконечно большом расстоянии, ЭМВ проходят через всю толщу атмосферы и наблюдения выполняют с поверхности Земли.

Продифференцируем первое выражение закона Гука два раза по x, второе два раза по y и третье по x и y. Получим следующие выражения

,

,

,

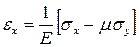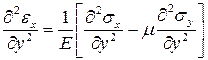
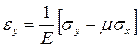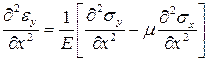
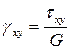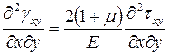
Подставим полученные производные в уравнение совместности деформаций.

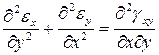
После сокращения на общий множитель получим

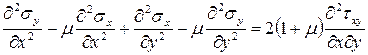(а)

Полученное уравнение является уравнением совместности деформаций в напряжениях. Чтобы исключить из этого выражения касательные напряжения, используем дифференциальные уравнения равновесия, дифференцируя первое по x, второе - по y.

,

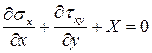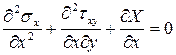
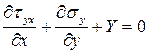
Складывая продифференцированные уравнения равновесия, выразим из них касательное напряжение

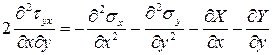
Подставим полученное выражение в (а)

,

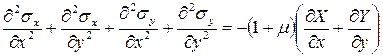которое после преобразований можно записать в виде

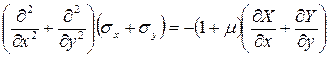
Получили окончательное уравнение совместности деформаций в напряжениях или уравнение Мориса Леви.

<== предыдущая страница | следующая страница ==>
Разрешающая система уравнений плоской задачи | Постановка задачи. Уравнение совместности деформаций в напряжениях и два дифференциальных уравнения равновесия образуют полную систему для определения неизвестных напряжений

Дата добавления: 2014-07-19; просмотров: 632; Нарушение авторских прав



Мы поможем в написании ваших работ!
lektsiopedia.org - Лекциопедия - 2013 год. | Страница сгенерирована за: 0.001 сек.