
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Разрешающая система уравнений плоской задачи
Лексический анализатор имеет дело с такими объектами, как различного рода константы и идентификаторы (к последним относятся и ключевые слова). Язык описания констант и идентификаторов в большинстве случаев является регулярным, то есть может быть описан с помощью регулярных грамматик. Распознавателями для регулярных языков являются конечные автоматы (КА). Существуют правила, с помощью которых для любой регулярной грамматики может быть построен КА, распознающий цепочки языка, заданного этой грамматикой.
Любой КА может быть задан с помощью пяти параметров: М (Q, V, d, q0, F), гдеq Q – конечное множество состояний автомата;q V – конечное множество допустимых символов (алфавит автомата);q d – функция переходов, отображающая V ´ Q (декартово произведение множеств) в множество подмножеств Q: R(Q), т.е. d (a, q)=R, a ÎV, qÎQ, RÍQ (R подмножество Q);q q0 – начальное состояние автомата, q0 Î Q;q F – непустое множество конечных состояний автомата, FÍQ, F¹0.КА называют полностью определенным , если в каждом его состоянии существует функция перехода для всех возможных входных символов, т.е. " а Î V (для всех а принадлежащих множеству V), "q Î Q $(существует) d(a, q)=R, RÍ Q. Работа КА представляет собой последовательность шагов. На каждом шаге работы автомат находится в одном из своих состояний Q (в текущем состоянии), на следующем шаге он может перейти в другое состояние или остаться в текущем. То состояние, в какое перейдет автомат на следующем шаге работы определяет функция переходов d. КА М (Q, V, d, q0, F) принимает цепочку символов wÎ V+, если, получив на вход эту цепочку, он из начального состояния q0 может перейти в одно из конечных состояний fÎF.Другим способом описания КА является граф переходов — графическое представление множества состояний и функции переходов КА. Граф переходов КА — это нагруженный однонаправленный граф,в котором вершины представляют состояния КА, дуги отображают переходы из одного состояния в другое, а символы нагрузки (пометки) дуг соответствуют функции перехода КА. Если функция перехода К А предусматривает переход из состояния q в q' по нескольким символам, то между ними строится одна дуга, которая помечается всеми символами, по которым происходит переход из q в q'.
Недетерминированный КА неудобен для анализа цепочек, так как в нем могут встречаться состояния, допускающие неоднозначность, то есть такие, из которых выходит две или более дуги, помеченные одним и тем же символом. Очевидно, что программирование работы такого КА — нетривиальная задача. Для простого программирования функционирования КА M(Q,S,d,q0,F) он должен быть детерминированным — в каждом из возможных состояний этого КА для любого входного символа функция перехода должна содержать не более одного состояния: "a|V, "q|Q: либо d(a,q) = {r} rÎQ, либо d(a,q) =Æ.
Доказано, что любой недетерминированный КА может быть преобразован в детерминированный КА так, чтобы их языки совпадали (говорят, что эти КА эквивалентны).
Кроме преобразования в детерминированный КА любой КА может быть минимизирован — для него может быть построен эквивалентный ему детерминированный КА с минимально возможным количеством состояний. Можно написать функцию, отражающую функционирование любого детерминированного КА. Чтобы запрограммировать такую функцию, достаточно иметь переменную, которая бы отображала текущее состояние КА, а переходы из одного состояния в другое на основе символов входной цепочки могут быть построены с помощью операторов выбора. Работа функции должна продолжаться до тех пор, пока не будет достигнут конец входной цепочки. Для вычисления результата функции необходимо по ее завершении проанализировать состояние КА. Если это одно из конечных состояний, то функция выполнена успешно и входная цепочка принимается, если нет, то входная цепочка не принадлежит заданному языку.
Однако в общем случае задача лексического анализатора шире, чем просто проверка цепочки символов лексемы на соответствие ее входному языку. Он должен правильно определить конец лексемы (об этом было сказано выше) и выполнить те или иные действия по запоминанию распознанной лексемы (занесение ее в таблицу лексем). Набор выполняемых действий определяется реализацией компилятора. Обычно эти действия выполняются сразу же при обнаружении конца распознаваемой лексемы.
Во входном тексте лексемы не ограничены специальными символами. Определение границ лексем — это выделение тех строк в общем потоке входных символов, для которых надо выполнять распознавание. Если границы лексем всегда определяются (а выше было принято именно такое соглашение), то их можно определить по заданным терминальным символам и по символам начала следующей лексемы. Терминальные символы — это пробелы, знаки операций, символы комментариев, а также разделители (запятые, точки с запятой и др.). Набор таких терминальных символов может варьироваться в зависимости от входного языка. Важно отметить, что знаки операций сами также являются лексемами и необходимо не пропустить их при распознавании текста.
Таким образом, алгоритм работы простейшего сканера можно описать так:
- просматривается входной поток символов программы на исходном языке до обнаружения очередного символа, ограничивающего лексему;
- для выбранной части входного потока выполняется функция распознавания лексемы;
- при успешном распознавании информация о выделенной лексеме заносится в таблицу лексем, и алгоритм возвращается к первому этапу;
- при неуспешном распознавании выдается сообщение об ошибке, а дальнейшие действия зависят от реализации сканера: либо его выполнение прекращается, либо делается попытка распознать следующую лексему (идет возврат к первому этапу алгоритма).
Работа программы-сканера продолжается до тех пор, пока не будут просмотрены все символы программы на исходном языке из входного потока.
(Диаграмма состояний (или иногда граф переходов) — графическое представление множества состояний и функции переходов. Представляет собой нагруженный однонаправленный граф, вершины которого — состояния КА, ребра — переходы из одного состояния в другое, а нагрузка — символы, при которых осуществляется данный переход. Если переход из состояния q1 в q2 может быть осуществлен при появлении одного из нескольких символов, то над дугой диаграммы (ветвью графа) должны быть надписаны все они.)
Разрешающая система уравнений плоской задачи
Опуская в разрешающей системе уравнений трехосной задачи отсутствующие слагаемые, имеем
1). Дифференциальные уравнения равновесия
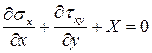 ,
,
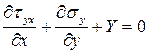
2). Связь напряжений в близи поверхности с нагрузкой. Условия на поверхности тела (Граничные условия)
 ,
,
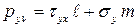
3). Выражения деформаций через перемещения. Формулы Коши
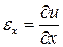 ,
, 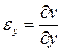 ,
, 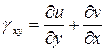
4).Уравнения совместности деформаций Сен-Венана
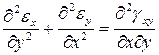
5). Выражение деформаций через напряжения. Закон Гука
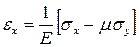 ,
, 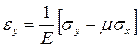 ,
, 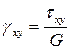
| <== предыдущая страница | | | следующая страница ==> |
| Построение лексических анализаторов (сканеров) | | | Выражение условия совместности деформаций через напряжения |
Дата добавления: 2014-07-19; просмотров: 432; Нарушение авторских прав

Мы поможем в написании ваших работ!