Построение лексических анализаторов (сканеров)

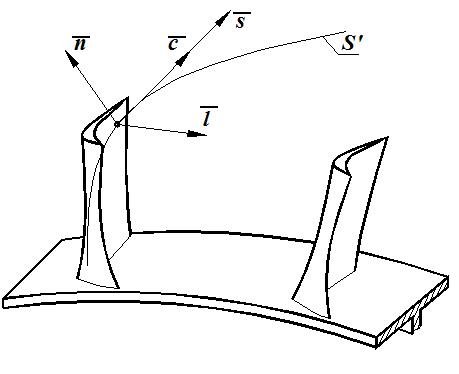
Рис. 2.4.

Рассмотрим некоторую частицу А в непосредственной близости от пера лопатки рабочего колеса:

с- абсолютная скорость частицы;

S’ – траектория частицы;

dm – масса частицы.

Определим направления:

n– нормаль к S в точке А;

s – касательная к S’ в точке А.

На векторахs, n достроим правую связку координат, назовём третью координату l.

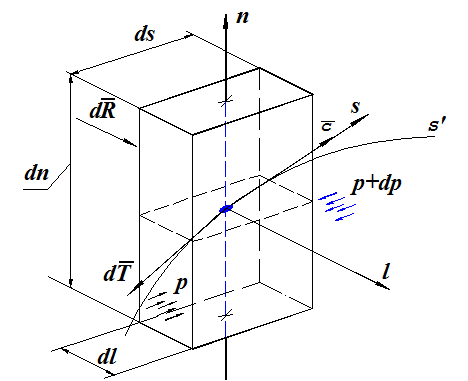
Рис. 2.5.

В координатах s n lпостроим бесконечно малый параллелепипед с геометрическим центром в точке А и массой dm = r.ds.dn.dl

Силы, действующие на частицу:

dP - сила давления

dT - сила трения, направлена по касательной к S

dR - сила, с которой лопатка воздействует на частицу

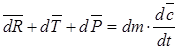По второму закону Ньютона:

Спроецируем это уравнение на ось Аs, перейдём к скалярным величинам.

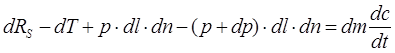
Перейдём к удельным величинам, т.е. разделим обе части уравнения на dm.

dR_S’ – удельная сила, с которой лопатки воздействует на рабочее тело;

dT’ – удельная сила трения;

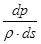- удельная сила давления.

Если удельную силу умножить на элементарный путь ds, то получим удельную работу

dR_S’.ds = dL_МЕХ

dT’.ds = dL_r – удельная работа трения

- работа по изменению давления, т.е. работа по расширению, которая совершает сама частица.

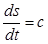
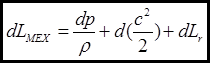(1)

Это уравнение сохранения энергии в механической форме в абсолютном движении в дифференциальном виде.Механическая работа идёт на работу по изменению сил давления, на изменение кинетической энергии потока и на работу по преодолению сил трения.

Теперь рассмотрим движение частицы на конечном участке пути от входа (1) до выхода 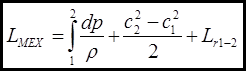(2)

(2)

Получили уравнение сохранения энергии в механической форме в абсолютном движении в интегральном виде.

Таблица лексем и содержащаяся в ней информация

Результатом работы лексического анализатора является перечень всех найденных в тексте исходной программы лексем с учетом характеристик каждой лексемы. Этот перечень лексем можно представить в виде таблицы, называемой таблицей лексем. Каждой лексеме в таблице лексем соответствует некий уникальный условный код, зависящий от типа лексемы, и дополнительная служебная информация. Таблица лексем в каждой строке должна содержать информацию о виде лексемы, ее типе и, возможно, значении. Обычно структуры данных, служащие для организации такой таблицы, имеют два поля: первое — тип лексемы, второе — указатель на информацию о лексеме.

Кроме того, информация о некоторых типах лексем, найденных в исходной программе, должна помещаться в таблицу идентификаторов (или в одну из таблиц идентификаторов, если компилятор предусматривает различные таблицы идентификаторов для различных типов лексем).

ВНИМАНИЕ:

Не следует путать таблицу лексем и таблицу идентификаторов — это две принципиально разные таблицы, обрабатываемые лексическим анализатором.

Таблица лексем фактически содержит весь текст исходной программы, обработанный лексическим анализатором. В нее входят все возможные типы лексем, кроме того, любая лексема может встречаться в ней любое количество раз. Таблица идентификаторов содержит только определенные тины лексем — идентификаторы и константы. В нее не попадают такие лексемы, как ключевые (служебные) слова входного языка, знаки операций и разделители. Кроме того, каждая лексема (идентификатор или константа) может встречаться в таблице идентификаторов только один раз. Также можно отметить, что лексемы в таблице лексем обязательно располагаются в том же порядке, что и в исходной программе (порядок лексем в ней не меняется), а в таблице идентификаторов лексемы располагаются в любом порядке так, чтобы обеспечить удобство поиска. В качестве примера можно рассмотреть некоторый фрагмент исходного кода на языке Object Pascal и соответствующую ему таблицу лексем, представленную в табл. 1:

begin for i:=1 to N do fg := fg * 0.5

Таблица 1 Лексемы фрагмента программы на языке Object Pascal

Поле «значение» в табл. 1 подразумевает некое кодовое значение, которое будет помещено в итоговую таблицу лексем в результате работы лексического анализатора. Конечно, значения, которые записаны в примере, являются условными. Конкретные коды выбираются разработчиками при реализации компилятора. Важно отметить также, что устанавливается связь таблицы лексем с таблицей идентификаторов (в примере это отражено некоторым индексом, следующим после идентификатора за знаком «:», а в реальном компиляторе определяется его реализацией).

Построение лексических анализаторов (сканеров)

Лексический анализатор имеет дело с такими объектами, как различного рода константы и идентификаторы (к последним относятся и ключевые слова). Язык описания констант и идентификаторов в большинстве случаев является регулярным, то есть может быть описан с помощью регулярных грамматик. Распознавателями для регулярных языков являются конечные автоматы (КА). Существуют правила, с помощью которых для любой регулярной грамматики может быть построен КА, распознающий цепочки языка, заданного этой грамматикой.

Другим способом описания КА является граф переходов — графическое представление множества состояний и функции переходов КА. Граф переходов КА — это нагруженный однонаправленный граф,в котором вершины представляют состояния КА, дуги отображают переходы из одного состояния в другое, а символы нагрузки (пометки) дуг соответствуют функции перехода КА. Если функция перехода К А предусматривает переход из состояния q в q' по нескольким символам, то между ними строится одна дуга, которая помечается всеми символами, по которым происходит переход из q в q'.

Недетерминированный КА неудобен для анализа цепочек, так как в нем могут встречаться состояния, допускающие неоднозначность, то есть такие, из которых выходит две или более дуги, помеченные одним и тем же символом. Очевидно, что программирование работы такого КА — нетривиальная задача. Для простого программирования функционирования КА M(Q,S,d,q₀,F) он должен быть детерминированным — в каждом из возможных состояний этого КА для любого входного символа функция перехода должна содержать не более одного состояния: "a|V, "q|Q: либо d(a,q) = {r} rÎQ, либо d(a,q) =Æ.

Доказано, что любой недетерминированный КА может быть преобразован в де­терминированный КА так, чтобы их языки совпадали (говорят, что эти КА эквивалентны).

Кроме преобразования в детерминированный КА любой КА может быть минимизирован — для него может быть построен эквивалентный ему детерминированный КА с минимально возможным количеством состояний. Можно написать функцию, отражающую функционирование любого детерминированного КА. Чтобы запрограммировать такую функцию, достаточно иметь пе­ременную, которая бы отображала текущее состояние КА, а переходы из одного состояния в другое на основе символов входной цепочки могут быть построены с помощью операторов выбора. Работа функции должна продолжаться до тех пор, пока не будет достигнут конец входной цепочки. Для вычисления результата функции необходимо по ее завершении проанализировать состояние КА. Если это одно из конечных состояний, то функция выполнена успешно и входная цепочка принимается, если нет, то входная цепочка не принадлежит заданному языку.

Однако в общем случае задача лексического анализатора шире, чем просто проверка цепочки символов лексемы на соответствие ее входному языку. Он должен правильно определить конец лексемы (об этом было сказано выше) и выполнить те или иные действия по запоминанию распознанной лексемы (занесение ее в таблицу лексем). Набор выполняемых действий определяется реализацией компилятора. Обычно эти действия выполняются сразу же при обнаружении конца рас­познаваемой лексемы.

Во входном тексте лексемы не ограничены специальными символами. Определение границ лексем — это выделение тех строк в общем потоке входных символов, для которых надо выполнять распознавание. Если границы лексем всегда определяются (а выше было принято именно такое соглашение), то их можно определить по заданным терминальным символам и по символам начала следующей лексемы. Терминальные символы — это пробелы, знаки операций, символы комментариев, а также разделители (запятые, точки с запятой и др.). Набор таких терминальных символов может варьироваться в зависимости от входного языка. Важно отметить, что знаки операций сами также являются лексемами и необходимо не пропустить их при распознавании текста.

Таким образом, алгоритм работы простейшего сканера можно описать так:

• просматривается входной поток символов программы на исходном языке до обнаружения очередного символа, ограничивающего лексему;
• для выбранной части входного потока выполняется функция распознавания лексемы;
• при успешном распознавании информация о выделенной лексеме заносится в таблицу лексем, и алгоритм возвращается к первому этапу;
• при неуспешном распознавании выдается сообщение об ошибке, а дальнейшие действия зависят от реализации сканера: либо его выполнение прекращается, либо делается попытка распознать следующую лексему (идет возврат к первому этапу алгоритма).

Работа программы-сканера продолжается до тех пор, пока не будут просмотрены все символы программы на исходном языке из входного потока.

(Диаграмма состояний (или иногда граф переходов) — графическое представление множества состояний и функции переходов. Представляет собой нагруженный однонаправленный граф, вершины которого — состояния КА, ребра — переходы из одного состояния в другое, а нагрузка — символы, при которых осуществляется данный переход. Если переход из состояния q1 в q2 может быть осуществлен при появлении одного из нескольких символов, то над дугой диаграммы (ветвью графа) должны быть надписаны все они.)

Дата добавления: 2014-07-19; просмотров: 567; Нарушение авторских прав

Мы поможем в написании ваших работ!