УРАВНЕНИЕ СОХРАНЕНИЯ ЭНЕРГИИ В МЕХАНИЧЕСКОЙ ФОРМЕ В АБСОЛЮТНОМ ДВИЖЕНИИ

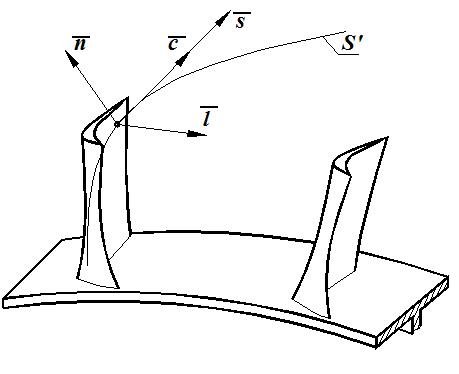
Рис. 2.4.

Рассмотрим некоторую частицу А в непосредственной близости от пера лопатки рабочего колеса:

с- абсолютная скорость частицы;

S’ – траектория частицы;

dm – масса частицы.

Определим направления:

n– нормаль к S в точке А;

s – касательная к S’ в точке А.

На векторахs, n достроим правую связку координат, назовём третью координату l.

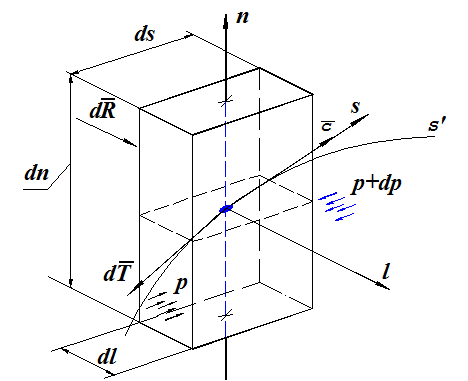
Рис. 2.5.

В координатах s n lпостроим бесконечно малый параллелепипед с геометрическим центром в точке А и массой dm = r.ds.dn.dl

Силы, действующие на частицу:

dP - сила давления

dT - сила трения, направлена по касательной к S

dR - сила, с которой лопатка воздействует на частицу

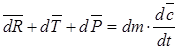По второму закону Ньютона:

Спроецируем это уравнение на ось Аs, перейдём к скалярным величинам.

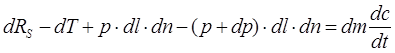
Перейдём к удельным величинам, т.е. разделим обе части уравнения на dm.

dR_S’ – удельная сила, с которой лопатки воздействует на рабочее тело;

dT’ – удельная сила трения;

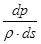- удельная сила давления.

Если удельную силу умножить на элементарный путь ds, то получим удельную работу

dR_S’.ds = dL_МЕХ

dT’.ds = dL_r – удельная работа трения

- работа по изменению давления, т.е. работа по расширению, которая совершает сама частица.

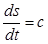
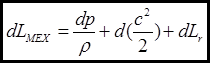(1)

Это уравнение сохранения энергии в механической форме в абсолютном движении в дифференциальном виде.Механическая работа идёт на работу по изменению сил давления, на изменение кинетической энергии потока и на работу по преодолению сил трения.

Теперь рассмотрим движение частицы на конечном участке пути от входа (1) до выхода 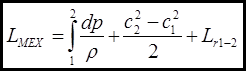(2)

(2)

Получили уравнение сохранения энергии в механической форме в абсолютном движении в интегральном виде.

Дата добавления: 2014-07-19; просмотров: 353; Нарушение авторских прав

Мы поможем в написании ваших работ!