
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Модуль 4. Задачи на построение
Задачи на построение занимают в геометрии особое место. Они имеют многовековую историю и часто являются интересными головоломками, для решения которых нужен особый подход. Они требуют умения читать чертежи, находить зависимость одних построений от других, составлять план пошагового решения. В то же время, для успешного решения сложных задач необходимо владеть на уровне автоматизма определенным базовым набором простейших элементарных задач на построение, так как в большинстве случаев решение сложной задачи сводится к решению более простой, уже известной ученику. Задачи на построение хорошо развивают логическое мышление, побуждают проявлять находчивость и творческий подход.
Напомним, что при решении задач на построение используются только два инструмента, линейка для проведения прямых линий и циркуль для проведения окружностей. Суть задач на построение: используя эти инструменты, построить некоторую фигуру по заданным условиям (обычно задаются геометрические фигуры и определенные соотношения между заданными фигурами и искомой). Решить задачу на построение – это значит свести ее к последовательности основных базовых построений.
Решение задач на построение состоит из 4 основных этапов: анализ, построение, доказательство (синтез), исследование.
Анализ. Это важный подготовительный этап, целью которого является составление плана решения. Для этого предполагают, что задача решена и выполняют приблизительный чертеж искомой фигуры «от руки». Внимательно изучая рисунок, находят зависимость между данными и искомыми величинами, которая позволила бы свести задачу к другим, уже известным задачам или найти положение искомого элемента.
На вспомогательном чертеже обычно по-разному выделяют данные и искомые элементы. Можно начинать набросок с искомой фигуры и пристраивать к ней заданные элементы в таком соотношении, как того требует условие задачи.
Построение. Последовательно выполняются те элементарные построения, которые следуют из плана решения задачи, составленного на этапе анализа. Любая задача на построение разбивается на конечное число шагов (простейших задач на построение).
Доказательство. Когда искомая фигура построена, необходимо доказать, что она удовлетворяет всем требованиям задачи. При этом ход рассуждений обычно обратный тому, который применялся при анализе.
Исследование проводится с целью выяснить полностью ли решена задача, сколько решений она имеет (одно или несколько), разрешима ли при всех допустимых значениях исходных данных. Необходимо рассмотреть всевозможные частные случаи, причем нужно выяснить, меняется ли ход решения в них и как именно. Полезно проводить исследование в соответствии с ходом построения; перебирая последовательно шаги, выяснить всегда ли действие выполнимо и сколькими способами.
Если задача имеет несколько решений, интересно рассмотреть разные способы построения искомой фигуры, сравнить их, обсудить преимущество и недостатки каждого.
Конечно, такая последовательность не является обязательной; какие-то этапы могут быть пропущены (например, анализ), какие-то объединены – это зависит от сложности задачи.
Для выполнения основных построений с помощью циркуля и линейки используется метод решения, при котором искомую точку строят как точку пересечения множеств (геометрических мест), определяемых некоторыми условиями.
Рассмотрим некоторые простейшие задачи на построение, относящиеся к базовым. Они не требуют подробного решения, последовательно проводимого по всем этапам. Но умение выполнять эти построения должно быть доведено до автоматизма, чтобы при решении более сложных задач не приходилось задумываться о простейших построениях.
Учителю. Прежде всего, надо освоить основные построения и отработать навыки в достаточном количестве задач, приучающих глаз и руку к построениям, не требующим анализа
Задание 1. Отложите на данной прямой отрезок данной длины а.
Учителю. Пусть данный отрезок будет только на Вашем листе, ученикам придется использовать циркуль, чтобы построить в своих тетрадях отрезок заданной длины. После построения попросите учеников проверить верность построения друг у друга.
Вопросы: Сколько отрезков заданной длины можно построить на прямой? (сколь угодно много)
Почему? (Прямая не ограничена)
Как изменится решение, если на прямой отметить точку и откладывать отрезок на данной прямой от данной точки? (можно будет построить только 2 отрезка заданной длины)
Задание 2. Начертите отрезок, равный сумме или разности двух данных отрезков а и b.
Решение. На произвольной прямой отметим точку А. Из точки А отложим в одну сторону отрезок АМ =а. Из точки А опишем окружность радиусом, равным b, получим точки В и С.
Отрезок МВ = а - в, если а > b, отрезок МС = а + b.
| М |
| В |
| А |
| С |
Вопрос. Как изменится построение, если а < b? (Начинать построение с большего отрезка b)
Учителю. Попросите учащихся провести построение отрезка а – b, если а < b, начиная с отрезка а. Предложите посчитать длину отрезка, если а =4; b =7.
| М |
| В |
| А |
| С |
Отметьте полученный отрезок на чертеже, и вспомните, что длина отрезка всегда положительное число и числовое значение длины «отрезка-разности» находится по модулю.
Задание 3. Данный отрезок разделите пополам.
| D |
| А |
| В |
| C |
| M |
Учителю. Ученики и седьмого и восьмого класса, конечно, умеют делить отрезок пополам. Поделите класс на группы по четыре ученика. Предложите первому ученику из группы взять радиус больше данного отрезка, второму – радиус равный отрезку, третьему – радиус больше половины отрезка, четвертому – радиус меньше половины отрезка. Используя циркуль с таким радиусом, каждый ученик пусть попробует выполнить процедуру деления отрезка. После этого ученики в группе сделают вывод. Обсудите.
В этой задаче полезно доказать, что полученные отрезки равны.
Доказательство. В седьмом классе доказательство проводится через равенство треугольников, а в восьмом классе можно проводить доказательство, используя свойства ромба. АСВD – ромб по построению, следовательно АМ=МВ по свойству диагоналей ромба.
Задание 4. Данный отрезок разделите на 4 равные части.
Решение. Разделить отрезок пополам, каждую половину отрезка разделить еще раз пополам.
Вопрос. Можно ли воспользоваться таким приемом для деления отрезка на другое количество равных частей? (Можно только на 2n частей).
Задание 5. Восставьте перпендикуляр к середине данного отрезка.
Учителю. Вернитесь к доказательству в задаче 3. Сделайте анализ, опираясь на этот чертеж.
Доказательство. Для седьмого класса доказательство проводится через равенство треугольников и смежные углы. Для восьмого класса: АСВD – ромб по построению и потому угол СМВ прямой по свойству диагоналей ромба.
Задание 6. А) Восставьте перпендикуляр к данной точке данной прямой.
Б) Опустите перпендикуляр из данной точки на данную прямую.
Учителю. Предложите учащимся провести анализ, опираясь на решение задания 5.
А) Анализ. Мы знаем, как восстановить перпендикуляр к середине отрезка. Следовательно, надо заданную точку сделать серединой какого-то отрезка, лежащего на заданной прямой. Для этого достаточно отложить от точки на прямой равные отрезки в обе стороны.
Б) Анализ. Для седьмого класса: два равных треугольника, у которых два угла смежные, являются прямоугольными, значит, общая сторона будет перпендикулярна прямой, содержащей две другие стороны смежных углов.
Для восьмого класса: диагонали ромба пересекаются под прямым углом и делятся точкой пересечения пополам. Построим ромб так, чтобы заданная точка была его вершиной, а две соседние вершины лежали на заданной прямой (проведем дугу, пересекающую прямую, с вершиной в заданной точке; найдем четвертую вершину ромба, проведя дуги тем же радиусом в другой полуплоскости).
Учителю. Рассмотрев задания 3 - 6, обсудите с учениками вопрос о геометрическом месте точек, равноудаленных от концов отрезка.
Вывод. Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину.
Задание 7. Разделите данный угол пополам.
Учителю. Построение и доказательство можно проводить как через равные треугольники, так и через ромб.
Задание 8. Разделите данный угол на 4 равные части.
Решение. Делим угол пополам. Затем каждый получившийся угол тоже пополам.
Вопрос. Можно ли воспользоваться таким приемом для деления угла на любое число равных частей. (Можно только на 2n частей).
Задание 9. Постройте треугольник по трем сторонам.
А) равносторонний;
Б) разносторонний.
Учителю. При построении разностороннего треугольника можно учащихся разбить на группы по три человека, каждому выдав свой набор отрезков для построения треугольника: сумма длин двух отрезков больше длины третьего; сумма длин двух отрезков равна длине третьего; сумма длин двух отрезков меньше длины третьего. Предложите ученикам обсудить полученные результаты и сделать вывод.
Задание 10. Постройте угол в 600.
Анализ. В равностороннем треугольнике все внутренние углы равны 600.
Решение. Построим равносторонний треугольник НВА. Угол АНВ = 600.
Задание 11. Постройте угол в 300.
Анализ (основываясь на задании 10). Если в точке Н к прямой НВ восстановить перпендикуляр, то угол, дополняющий угол АНВ до прямого будет равен 300.
| Н |
| А |
| В |
| С |
Решение. Проведем прямую, восстановим к ней перпендикуляр в любой точке. Отметим точку Н – основание перпендикуляра. Построим равносторонний треугольник НВА. Угол АНВ = 600, значит, угол СНВ равен 300.
Задание 12. Разделите прямой угол на три равных части.
Анализ (основываясь на задании 11).
1. Достаточно разделить угол АНВ пополам.
2. Если мы построим равносторонний треугольник с вершиной в точке Н и стороной, лежащей на луче НС, то от луча НС будет отложен угол в 600. Угол СНВ будет разбит на 3 равных части.
| Н |
| N |
| В |
| А |
| M |
Решение. Проведем прямую, восстановим к ней перпендикуляр в любой точке. Отметим точку Н – основание перпендикуляра. С центром в точке Н любым радиусом проведем дугу, пересекающую стороны прямого угла, получим точки А и В. Из точек А и В этим же радиусом сделаем засечки на дуге АВ, получим точки М и N.
Проведем лучи НМ и НN, они разобьют прямой угол на три равных части.
Доказательство. Угол АНN =300, угол ВНМ = 300. Значит, МНN = 300.
ÐАНМ =ÐВНN = ÐМНN = 300. Значит, прямой угол поделили на три равные части.
Задачу о делении угла на три равные части пытались решить еще в Древней Греции. Трисекция угла, удвоение куба и квадратура круга – эти три классические задачи оказалось невозможно решить с помощью циркуля и линейки.
Рассмотрим несколько задач на построение треугольника. Считаем, что три основных задачи на построение треугольников уже хорошо усвоены, и они используются как базовые.
Задание 13. Постройте треугольник по данной стороне, углу, к ней прилежащему, сумме двух других сторон.
Анализ: Пусть треугольник АВС – искомый. Известны угол А, сторона b и длина а+с. Продолжим АВ так, чтобы AD = а+с. Соединим C и D.
Треугольник АCD можно построить по двум сторонам и углу между ними: АD = а+c, АC = b, ÐСАD = ÐА. Треугольник CВD – равнобедренный: ВН – высота, медиана. Проведя серединный перпендикуляр ВН к CD, определяем вершину В.
| А А А А А А А А |
| с с с с с с с с |
| В В В В В В В В |
| а а а а а а а а |
| D D D D D D D D |
| Н Н Н Н Н Н Н Н |
| С С С С С С С С |
| b b b b b b b b |
| a a a a a a a a |
Построение.
1) Строим треугольник АCD по двум сторонам и углу между ними: АD = а+c, АC = b, ÐСАD = ÐА.
2) К отрезку CD проводим серединный перпендикуляр ВН до пересечения со стороной АD, получаем вершину В.
Треугольник АВС – искомый.
Доказательство. ΔВНС = Δ ВHD (по катетам), следовательно, ВС=ВD.
Т.к. АD = а+c, то АВ+ВС= АD = а+c. ΔАВС – искомый.
Исследование. Построение выполнимо, если работает неравенство треугольника.
| А А |
| С С |
| В В |
| Н1 Н1 Н1 Н1 Н1 Н1 |
| Н2 Н2 Н2 Н2 Н2 Н2 |
Анализ. Пусть треугольник АВС – искомый. Известны угол А, сторона b и расстояние h от точки В до стороны АС. Проведем прямую параллельно АС так, чтобы расстояние между ними равнялось h, она пройдет через точку В.
Построение.
1) Построим ÐА. На одной из сторон отложим отрезок АС= b.
2) Построим перпендикуляры АН1=h и СН2=h к прямой АC, проведем прямую Н1Н2. Прямая Н1Н2 пересечет вторую сторону ÐА, получим вершину В.
| А А |
| С С |
| В2 В2 В2 В2 В2 В2 |
| В1 В1 В1 В1 В1 В1 |
| В3 В3 В3 В3 В3 В3 |
Доказательство. Н1Н2 ││АС по построению. Проведем высоту треугольника ВН.
ВН = АН1 =h .
ΔАВС – искомый.
Исследование. Возможны три ситуации:
· если h = b tgA, то треугольник АВС прямоугольный;
· если h < b tgA, то треугольник АВС остроугольный;
· если h > b tgA, то треугольник АВС тупоугольный.
Задание 15. Постройте прямоугольный треугольник по гипотенузе с и сумме катетов а+b.
Анализ. Пусть треугольник АВС – искомый. Известны: ÐС =900, гипотенуза с и отрезок а+b, равный сумме катетов. Продолжим АС так, чтобы отрезок AD = а+b. Получим треугольник АВD – равнобедренный, в котором ÐВ = ÐD = 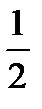 ÐС = 450 по свойству внешнего угла треугольника. Треугольник АВD можно построить по двум сторонам и углу: АD = а+b, АВ =с, ÐАDВ = 450. Построив перпендикуляр ВС, получим вершину С.
ÐС = 450 по свойству внешнего угла треугольника. Треугольник АВD можно построить по двум сторонам и углу: АD = а+b, АВ =с, ÐАDВ = 450. Построив перпендикуляр ВС, получим вершину С.
Построение.
1) Строим треугольник АВD по двум сторонам и углу: АD = b+а, АВ = с и ÐD = 450.
2) Из точки В опускаем перпендикуляр на сторону АD, находим вершину С.
Треугольник АВС – искомый.
Доказательство. По построению ΔВDС – прямоугольный с углом 450, следовательно, он равнобедренный, т.е. ВС=DC. Значит, треугольник АВС – искомый.
Исследование. Построение выполнимо, если не нарушено неравенство треугольника.
Задание 16. Постройте прямоугольный треугольник по гипотенузе и высоте, опущенной на гипотенузу.
| А А |
| В В |
| С1 С1 |
| С2 С2 |
| h h |
| c c |
Анализ. Пусть прямоугольный треугольник АВС – искомый. Известны: ÐС =900, гипотенуза с и расстояние h от точки С до стороны АВ. Опишем окружность около ΔАВC. АВ – диаметр. Проведем прямую параллельно АВ так, чтобы расстояние между ними равнялось h, она пройдет через С.
Построение.
1) Построим окружность с диаметром АВ = с.
2) Восстановим перпендикуляры АН1=h и ВН2=h в точках А и В прямой АВ, проведем прямую Н1Н2. Прямая Н1Н2 пересечет окружность, получим вершину С.
3) Соединим точку С с точками А и В. Треугольник АВС – искомый.
Доказательство. Треугольник АВС по построению прямоугольный с гипотенузой с.
Н1Н2││АВ по построению. Проведем высоту треугольника СН. СН = АН1=h. ΔАВС – искомый.
Исследование. Возможны три случая:
· если h = 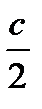 , то треугольник АВС равнобедренный, единственный, лежащий по одну сторону от гипотенузы (конечно, можно проводить построение и в другую полуплоскость относительно диаметра окружности, но мы построим треугольник, полученный из первого осевой симметрией; следовательно, в этом случае мы говорим о единственном решении);
, то треугольник АВС равнобедренный, единственный, лежащий по одну сторону от гипотенузы (конечно, можно проводить построение и в другую полуплоскость относительно диаметра окружности, но мы построим треугольник, полученный из первого осевой симметрией; следовательно, в этом случае мы говорим о единственном решении);
· если h < 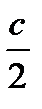 ,то получим два равных треугольника АВС1 и АВС2, лежащих по одну сторону от гипотенузы (в этом случае мы получаем два решения, так как треугольники равны, но в них АС1=ВС2, а ВС1=АС2, то есть один треугольник нельзя получить из другого тождественным преобразованием).
,то получим два равных треугольника АВС1 и АВС2, лежащих по одну сторону от гипотенузы (в этом случае мы получаем два решения, так как треугольники равны, но в них АС1=ВС2, а ВС1=АС2, то есть один треугольник нельзя получить из другого тождественным преобразованием).
· если h > 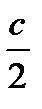 ,то решений нет.
,то решений нет.
Задание 17. Постройте треугольник по основанию и углу при вершине.
Анализ. Пусть треугольник АВС – искомый. Известны: Ð В и сторона b.
| А А |
| В В |
| С С |
| О О |
| h h |
| b b |
| М М М М М М М М |
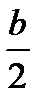 ) и углу (ÐВ).
) и углу (ÐВ).
Построение.
1) Построим прямоугольный ΔАОМ по катету АМ = и ÐАОМ = ÐВ.
2) Построим окружность радиуса ОА, продолжим сторону АМ до пересечения с окружностью, полученный отрезок АС = b. Отметим любую точку, лежащую на окружности, получим вершину В.
Треугольник АВС – искомый.
Доказательство. ÐАВС=ÐАОМ как вписанный, следовательно, ÐАВС=ÐВ.
ΔАВС – искомый.
Исследование. Возможны два случая:
· если точку В выбираем по одну сторону от АС (в полуплоскости, содержащую точку О), то получаем множество треугольников, удовлетворяющих заданным условиям;
· если точку В выбираем по другую сторону от АС, то получаем треугольники, не удовлетворяющие условию, так как у них ÐАВС= 1800 - ÐВ; искомых треугольников нет.
Задание 18. Постройте треугольник по двум углам и периметру.
| А А |
| В В |
| С С |
| D D |
| Е Е |
| b b |
| c c |
| a a |
| a a |
| c c |
| К К |
| Н Н |
Анализ. Пусть треугольник АВС – искомый. Известны: ÐА и ÐС и отрезок длиной а+b+с. На продолжении стороны АС в обоих направлениях отложим отрезки DA = АВ и СЕ = ВС, проведем отрезки DВ и ВС, получим треугольник DВE, в котором DE = а+b+с. Треугольники DAВ и ВСЕ – равнобедренные, опустим высоты (серединные перпендикуляры) АК и СН (этопозволит определить вершины А и С при построении). ÐD =
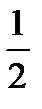 ÐА, ÐЕ =
ÐА, ÐЕ = 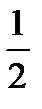 ÐС (по свойству внешнего угла треугольника). Задача сводится к построению треугольника DВE по стороне и двум прилежащим углам.
ÐС (по свойству внешнего угла треугольника). Задача сводится к построению треугольника DВE по стороне и двум прилежащим углам.
Построение.
1) Строим треугольник ВDЕ: DЕ = а+ b+ c, ÐВDЕ = 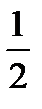 ÐА, ÐВЕD =
ÐА, ÐВЕD =  ÐС.
ÐС.
2) Проводим серединные перпендикуляры АК к ВD и СН к ВE. Получаем вершины А и С.
Треугольник АВС – искомый.
Доказательство.
1) При построении получаем:
1. Треугольник ВАD: ВК=КD, АК перпендикулярен ВD, следовательно, треугольники АКВ = АКD (по катетам), следовательно AD=ВA.
2. Треугольник ВCЕ: ВН=НE, СН перпендикулярен ВE, следовательно, треугольники BCН = BEН (по катетам), следовательно ВC=ВE.
2) DE = DA+AС+СE = CA+AС+BC = а+ b+ c,
Значит, треугольник АВС – искомый.
Исследование. Построение выполнимо если ÐС + ÐА < 1800.
Задание 19. Постройте треугольник по высотам hа и hb и медиане mс.
Анализ. Пусть треугольник АВС – искомый. Известны: АЕ =hа и ВН= hb и СМ = mс.
ÐВСА =ÐВСМ + ÐАСМ.
МК 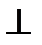 АС. МК=
АС. МК= 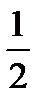 ВН=
ВН= 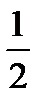 hb. Получаем прямоугольный ΔСКМ, который можно построить по катету и гипотенузе СМ = mс.
hb. Получаем прямоугольный ΔСКМ, который можно построить по катету и гипотенузе СМ = mс.
| А А |
| В В |
| С С |
| М М |
| Е Е |
| Н Н |
| K K |
| L L |
LМ
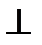 BС. LМ =
BС. LМ = 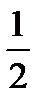 AE =
AE = 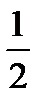 ha. Получим ΔСLМ – прямоугольный, его можно построить по катету и гипотенузе СМ = mс.
ha. Получим ΔСLМ – прямоугольный, его можно построить по катету и гипотенузе СМ = mс.
Построение.
1) Построим прямоугольный ΔСКМ с катетом КМ = 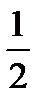 ВН =
ВН = 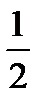 hb и гипотенузой СМ = mс.
hb и гипотенузой СМ = mс.
2) Построим прямоугольный ΔСLМ с катетом LМ = 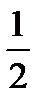 AE =
AE = 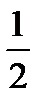 ha и гипотенузой СМ = mс, причем так, чтобы точки К и L лежали по разные стороны от прямой СМ.
ha и гипотенузой СМ = mс, причем так, чтобы точки К и L лежали по разные стороны от прямой СМ.
3) Продолжим отрезок КМ за точку M так, чтобы отрезок КN = 2 КМ = ВН и проведем через точку N прямую, параллельную КС. Продолжим CL до пересечения с этой прямой. Получим вершину В.
4) Проведем прямую ВМ и найдем пересечение ее с прямой СК. получим вершину А.
| А А |
| В В |
| С С |
| М М |
| Е Е |
| Н Н |
| K K |
| L L |
| N N |
Доказательство.
СМ = mс по построению. КN = ВН = hb. DАКМ = DМNB (по катету и острому углу), отсюда АМ=МВ. Из точки А опустим высоту на сторону ВС, она параллельна МL. МL – средняя линия в треугольнике АВЕ,
и АЕ = 2МL = ha.
ΔАВС – искомый.
Исследование. Если 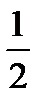 hb > mс , то решений нет.
hb > mс , то решений нет.
| <== предыдущая страница | | | следующая страница ==> |
| | | ОБЪЕКТИВНАЯ НЕОБХОДИМОСТЬ ПСИХИКИ |
Дата добавления: 2014-11-01; просмотров: 698; Нарушение авторских прав

Мы поможем в написании ваших работ!