Уравнения совместности деформаций

Величин относительных деформаций 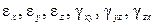выражены через 3 величины осевых перемещений (u, v, w). Деформации не являются независимыми величинами и связаны между собой некоторыми отношениями. Установим их и с этой целью выпишем из (5.3) выражения

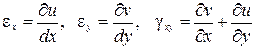
для деформаций, содержащих только индексы х и y, и найдем вторые производные от них:

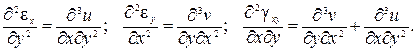
Отсюда следует, что

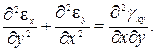
Тем самым получено первое из искомых уравнений.

Аналогично поступая с деформациями, содержащими только индексы у и z, а также z и х,можно получить еще 2 родственных соотношения, которые вместе с первым образуют следующую группу уравнений:

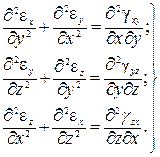(5.21)

Исследуя структуру этих уравнений, также как и структуру формул (5.3), не трудно заметить, что пе­реход от одного уравнения к другому совершается по правилу циклической перестановки индексов и букв (рис. 5.6):

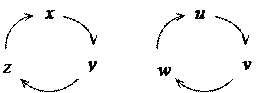
Рис.5.5

Продифференцируем каждую из угловых деформаций, выражаемых формулами (5.3):

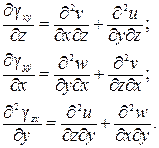
Затем алгебраически просуммируем, правые и левые части этих равенств, беря два из них со знаком плюс, а третье – со знаком минус. Такое суммирование возможно в 3-х вариантах(знак минус поочередно «пробегает» по всем трем строкам). Например, если возьмем со знаком минус вторую строку, а первую и третью – со знаком плюс, то почленное сложение дает уравнение:

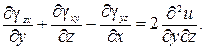
Нужно добиться того, чтобы в полученном равенстве ис­чезли перемещения и остались только деформации. Это достигается дифференцированием обеих частей полученного равенства по координате х. При этом в правой части появится производная 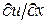=. В результате имеем:

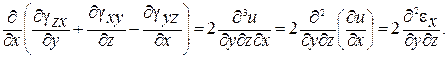
Два других уравнения 2-й группы выводятся аналогич­но. Кроме того, их также можно получить из данного уравнения посредством циклической перестановки индексов. уравнения 2-й группы представим системой трех уравнений:

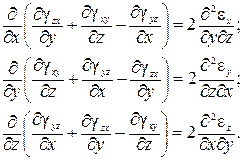(5.21)

уравнения, представленные выражениями (5.19) и (5.20), показывает связь деформации между собой. В названии уравнений участвуют четыре следующие вариации различных, но равноправных терминов:

уравнения неразрывности деформаций;

условия неразрывности деформаций;

уравнения совместности деформаций;

условия совместности деформаций.

данные уравнения называют уравнениями Сен-Венана.

Физический смысл уравнений Сен-Венана заключается в том, что при их удовлетворении упругое тело деформирутся без нарушения сплошности материала, т. е. без образования в нем пор и разрывов. Отсюда еще одно (шестое) название – условия сплошности. Но каждая вариация этих названий отражает различные оттенки смысла, которые вкладываются в эти уравнения при их практическом использовании.

 

 

---

<== предыдущая страница	|	следующая страница ==>
Диаграмма Мора для деформаций	|

---

Дата добавления: 2014-03-03; просмотров: 1645; Нарушение авторских прав

---

Поделиться с ДРУЗЬЯМИ:

Мы поможем в написании ваших работ!