
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Деформаций и напряжений
Математическая Аналогия теорий
Исследуя удлинение произвольно выбранного волокна, направление r которого образует углы α, β, γс осями системы координат Oxyz, можно получить следующее выражение для удлинения εr по направлению r:
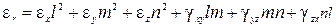 , (5.7)
, (5.7)
где величины
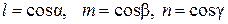
называются направляющими косинусами исследуемого волокна. Из выражения (2.7) следует, что удлинение dr произвольного волокна, проходящего через заданную точку, можно выразить через шесть компонентов тезора деформации в той же точке.
Сравнивая между собой выражения (3.10) и (5.7), обнаружим, что они математически подобны.
Можно строго доказать, что между теорией напряжений и теорией деформаций имеется полная математическая аналогия. Следовательно, необходимые формулы в теории деформаций можно выражать аналогично соответствующим формулам в теории напряжений.  Тогда в каждой точке упругого элемента существует три взаимно перпендикулярные направления волокон, между которыми углы при их деформировании остаются прямыми. Относительные удлинения ε1, ε2, ε3 таких волокон называются главными удлинениями, их направления 1, 2 и 3 – главными осями деформации в точке, а плоскости, перпендикулярные к главным осям, – главными плоскостями деформированного состояния в той же точке упругого тела.
Тогда в каждой точке упругого элемента существует три взаимно перпендикулярные направления волокон, между которыми углы при их деформировании остаются прямыми. Относительные удлинения ε1, ε2, ε3 таких волокон называются главными удлинениями, их направления 1, 2 и 3 – главными осями деформации в точке, а плоскости, перпендикулярные к главным осям, – главными плоскостями деформированного состояния в той же точке упругого тела.
| Угловые деформации в главных плоскостях отсутствуют. |
При совпадении осей x, y, z с направлением главных осей 1, 2, 3 в формуле (5.7) угловые деформации надо принять равными нулю и заменить буквенные индексы цифровыми. В результате получим:
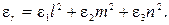 (5.8)
(5.8)
Следовательно, для осей, совпадающих с главными осями деформации, тензор деформаций (5.5) примет вид, аналогичный тезору (3.15):
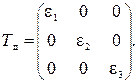 (5.9)
(5.9)
При этом значения главных удлинений располагаютак же , как напряжения: ε1>ε2>ε3.
В упругом изотропном теле направления главных деформаций ε1, ε2, ε3 совпадают с направлениями главных напряжений σ1, σ2, σ3, так как нет причин для того, чтобы симметричная система главных напряжений вызывала несимметричную картину деформаций.
| Среди множества наклонных площадок в теории выделяются площадки одинаково наклоненные к трем главным площадкам, которые называются октаэдрическими площадками. |
Продолжая аналогию, выразим удлинения в направлении, нормальном к октаэдрическим площадкам, подобно выражению (3.18):
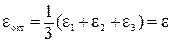 , (5.10)
, (5.10)
Для угловых деформаций в октаэдрических площадках по аналогии с (3.19) имеем формулу
 (5.11)
(5.11)
Для наибольшего сдвига по аналогии с (3.16) получим выражение
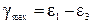 . (5.12)
. (5.12)
| <== предыдущая страница | | | следующая страница ==> |
| Тензор деформаций | | | Деформированного состояния |
Дата добавления: 2014-03-03; просмотров: 548; Нарушение авторских прав

Мы поможем в написании ваших работ!