Основы расчета теплообменных аппаратов

Для того чтобы определить теплоту, передаваемую в единицу времени от одного теплоносителя к другому, необходимо воспользоваться зависимостью

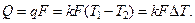(14.1)

Здесь F — площадь теплообмена; k — коэффициент теплопередачи, Вт/(м²∙K).

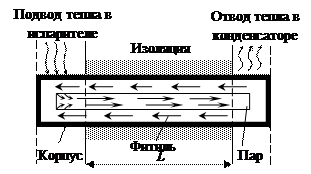
Рис. 14.5. Тепловая труба горизонтального действия

Если допустить, что теплообмен осуществляется через плоскую стенку, то согласно (12.7)

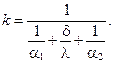
Величина ΔТ называется температурным напором и является разностью температур теплоносителей. При решении уравнения полагается, что ΔТ=const. В действительности эта величина меняется по длине теплообменника. Возникает вопрос: как определить температурный напор?

Рассмотрим рекуперативный прямоточный теплообменник (см. рис. 14.2). Если выполняется условие ΔТ_н/ΔТ_к<2, то можно пользоваться среднеарифметическим значением температурного напора:

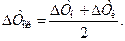
Ошибка расчетов при этом не превышает 4%.

Покажем, как определяется точное значение температурного напора.

Рассмотрим теплообмен на маленьком участке теплообменника с площадью dF. Температура каждого теплоносителя на этом участке изменяется на величину dT (рис. 14.6).

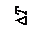
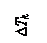
Рис. 14.6. К расчету прямоточного теплообменного аппарата

При этом теплота, передаваемая на этом участке, равна:

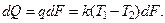(14.2)

При этом от первого теплоносителя отбирается (учтем это знаком минус) теплота 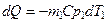, а второму передается 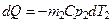. Здесь 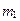и — массовые расходы теплоносителей. Отсюда следует, что

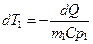и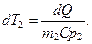

Тогда

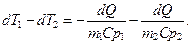
или

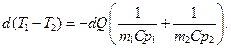(14.3)

С учетом (14.2) выражение (14.3) примет вид

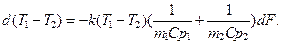
Отсюда

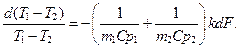(14.4)

В целом от первого теплоносителя отбирается теплота

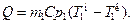
Такое же количество тепловой энергии передается второму теплоносителю

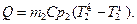
Из этого следует, что

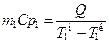и 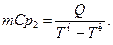(14.5)

Подставим (14.5) в (14.4) и после преобразования получим

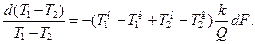
Из рис. 14.6 видно, что

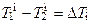и ,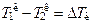

т. е.

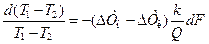
или

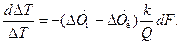(14.6)

Проинтегрируем выражение (14.6) по F от нуля до F и по ΔТ от ΔТ_н до ΔТ_к

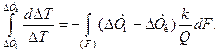
Поменяв пределы интегрирования в левой части, получим

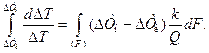(14.7)

После интегрирования (14.7) имеем

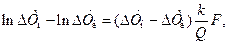
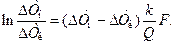
Отсюда

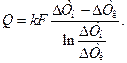(14.8)

Сравним выражения (14.1) и (14.8) и придем к выводу, что

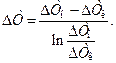(14.9)

Величина в выражении (14.9) называется среднеинтегральным температурным напором.

Итак, среднеинтегральный температурный напор — это отношение разности температурных напоров на входе и выходе из теплообменника к натуральному логарифму отношения этих напоров.

Однако определение ΔТ в такой трактовке справедливо только для теплообменников прямоточной схемы. В случае противотока (см. рис. 14.2, а) вход одного теплоносителя является выходом другого. Грубой (но вместе с тем и типичной) ошибкой при этом является то, что по аналогии с вышесказанным берут разность температур теплоносителей на разных концах труб.

В действительности же для схемы с противотоком 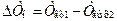, а 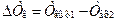, т.е. необходимо брать разности температур на концах теплообменника. Если при этом окажется, что 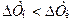, то в выражении (14.9) отрицательными будут и числитель, и знаменатель, а в целом ΔТ<0.

Таким образом, определив температурный напор, по формуле (14.9) можно определить количество теплоты, передаваемой в теплообменнике.

Вторым уравнением для расчета теплообменника является уравнение теплового баланса

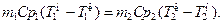(14.10)

Повторим, что равенство (14.10) справедливо при допущении, что не учитываются утечки теплоты в окружающую среду. На самом деле эти потери достигают 10%.

В уравнении (14.10) можно определить только одну неизвестную величину, например, расход теплоносителя или его конечную температуру, полагая, что все остальные величины известны. На практике, как правило, многие из величин, входящих в уравнение (14.10), являются неизвестными. Это не позволяет напрямую использовать данную зависимость для расчетов.

Различают конструктивный и поверочный расчет теплообменника.

Конструктивный расчет ведется по следующему алгоритму:

1. Исходной величиной для расчета является мощность теплообменника, т. е. количество теплоты, передаваемой теплоносителю в единицу времени.

2. По справочной литературе задаются скоростями движения теплоносителя (обычно принимают скорость W≈1 м/с) и конструктивными особенностями теплообменника (диаметром и материалом труб, площадью проходного сечения и т. д.). Это позволяет определить расход теплоносителя ( 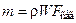). Задаваясь температурой теплоносителя на входе в теплообменник, из (14.10) определяют его температуру на выходе.

3. По соответствующему критериальному уравнению Nu=f(Re, Pr,…)определяют коэффициенты теплоотдачи теплоносителей, а затем и коэффициент теплопередачи

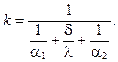
4. По формуле (14.9) определяют среднеинтегральный температурный напор.

5. Из уравнения (14.1) определяют требуемую площадь теплообмена F.

6. По значению F устанавливают число труб в теплообменнике и их длину.

После конструктивного расчета проводят поверочный расчет по следующему алгоритму:

1. Задаются конечной температурой одного из теплоносителей на выходе из теплообменника.

2. Считая, что температуры теплоносителей на входе заданы, из (14.10) определяют температуру на выходе второго теплоносителя.

3. Далее, повторяя алгоритм конструктивного расчета (пп. 3—6), определяют площадь теплообмена F . В случае расхождения результатов конструктивного и поверочного расчетов более чем на 10% весь расчет повторяют сначала.

Дата добавления: 2014-08-04; просмотров: 497; Нарушение авторских прав

Мы поможем в написании ваших работ!