Работа, энергия, мощность

Силы служат причиной либо ускорения тела (динамическое действие), либо изменения его формы (статическое действие).

Если сила перемещает тело на некоторое расстояние, то она совершает над телом работу.

Работа = Сила х Перемещение.

При F = const (в случае постоянной силы в процессе перемещения) A = F s, в случае переменной силы – интеграл от силы по перемещению A = .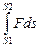

Мощность – отношение произведенной работы на время, в течение которой она произведена:

Мощность = Работа / Время.

Мгновенная мощность – производная работы по времени: Р = dA/dt. Поскольку dA = Fds (сила на перемещение), то Р = Fds/dt = Fv. Мгновенная мощность равна произведению мгновенной силы на мгновенную скорость.

Энергия – способность тела совершать работу, единая мера различных форм движения. Количественные характеристики зависят от вида энергии (механическая, внутренняя, химическая, ядерная, электромагнитная и др.).

Два способа передачи движения и соответствующей ему энергии от одного тела к другому – в форме работы и в форме теплоты (путем теплообмена). Для микрочастиц (атомы, электроны) эти понятия неприменимы.

Работа против силы тяжести.

Если тело движется в направлении действия силы тяжести, то над телом совершается работа A = G h или A_т = mg h.

Чтобы поднять тело (увеличить расстояние от центра Земли), над ним следует совершить работу. Работа, совершаемая силой F при движении против силы тяжести (подъеме тела) на высоту h не зависит от пути – зависит только от того, насколько тело может опуститься до заданного уровня. Эта работа запасается в виде потенциальной энергии тела (энергии положения) A =W_п = mgh, равной работе, затраченной на подъем тела.

Это не полная потенциальная энергия – только приращение энергии при подъеме тела на высоту (начало отсчета выбирается произвольно). С учетом изменения гравитационного поля по высоте

W_п = m .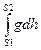

Потенциальной энергией называется энергия, зависящая только от взаимного расположения материальных точек (или тел).

Силы, действующие на материальную точку (тело), называются потенциальными, если работа этих сил при перемещении точки (тела) зависит только от начального и конечного положения точки (тела) в пространстве и не зависит от пути перемещения.

Во всех физических явлениях важна не сама потенциальная энергия, а ее изменение, которым определяется совершаемая работа. Уровень отсчета изменений заранее оговаривается.

Потенциальная энергия включает энергию положения и энергию упругой деформации.

Потенциальной энергией может обладать не только система взаимодействующих сил, но и отдельно взятое упруго деформируемое тело (сжатая пружина, растянутый стержень). В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела (витков пружины).

Потенциальной энергией может обладать не только система взаимодействующих сил, но и отдельно взятое упруго деформируемое тело (сжатая пружина, растянутый стержень). В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела (витков пружины).

Кинетическая энергия тела является мерой его механического движения и измеряется той работой, которую может совершить тело при торможении до полной остановки.

Из состояния покоя изменение скорости и пути к моменту t: V=at, S=Vt/2=at²/2.

При торможении на тело действует сила, направленная против его движения.

До полной остановки тело под действием силы F совершит работу А: А = Fs = F v²/2a = mv²/2.

Кинетическая энергия тела К = mv²/2

При подъеме на высоту накопилась потенциальная энергия W_п, при падении с этой высоты эта потенциальная энергия превратилась в кинетическую W_к. W_п= W_к = mgh = mv²/2.

Работа, затрачиваемая на ускорение.

Если под действием постоянной силы F_уск тело равномерно ускоренно перемещается на расстояние s, то над ним совершается работа A_уск = F_уск s = mas.

Если ускорение сообщается телу, находящемуся в состоянии покоя, совершаемая над телом работа запасается в виде кинетической энергии W_к = mv²/2.

Кинетическая энергия тела К = mv²/2 – в случае поступательного движения тела со скоростью v.

В случае вращения под действием момента силы закрепленное на оси твердое тело приобретает угловое ускорение.

Полный момент М = 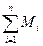= 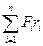. Так как Fr = m a r = m ∆v/∆t r = m r ∆w/∆t r = mr²a, то

М = a 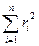∆m_i = М = I a.

a - угловое ускорение, одинаковое у всех элементов массы тела. Или I = М / a.

Момент инерции тела I зависит от распределения массы тела относительно оси вращения.

Момент инерции тела относительно оси – мера инертности тела во вращательном движении вокруг этой оси, и равна сумме произведений масс всех частиц тела на квадраты их расстояний относительно той же оси. Зависит только от формы тела и расположения частиц в нем.

Поскольку работа равна силе на перемещение, то в случае вращательного движения А =Мj, где М – момент силы F, j - угловое перемещение тела.

Если тело вращается вокруг неподвижной оси, то его кинетическая энергия К = Jw²/2, где J – момент инерции тела, w - угловая скорость.

W_вр – энергия вращательного движения (величина тангенциального ускорения – силы Кориолиса, если тело движется по радиусу во вращающейся системе отсчета). Перемещение тела в радиальном направлении r = vt, где v – скорость по радиусу. Точка за это время пройдет по пути окружности s = rωt = vωt² = at²/2, где ω – угловая скорость вращающейся системы.

Работа против сил трения.

Движущееся тело теряет энергию из-за наличия трения, которое действует на поверхности соприкосновения тел и и затрудняет их перемещение относительно друг друга.

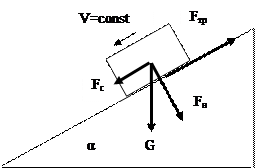Сила трения направлена вдоль поверхности соприкосновения в сторону, противоположную движению F_тр = μF_н, где μ – коэффициент трения, F_н – нормальная сила, которая прижимает тело к опоре (не зависит от площади соприкосновения тел).

μ = tgα (при каком угле наклона тело начинает двигаться).

Сила трения равна скатывающей силе F_тр = F_с.

Виды трения:

покоя (μ₀), скольжения (μ_ск< μ₀), качения (μ_к<< μ₀).

Если тело движется с постоянной скоростью равномерно против сил трения, то над ним совершается работа A_тр = F_тр s = μF_н s.

Работа против сил трения превращается в тепловую энергию.

Работа, затрачиваемая на упругую деформацию тела.

Согласно законам Ньютона все изменения состояния движения вызываются силами. Силы служат причиной либо ускорения тела (динамическое действие), либо изменения его формы (статическое действие).

Внешние силы изменяют форму тела – деформируют его вследствие относительного смещения элементов (молекул). Деформации, исчезающие с приращением действия силы – упругие деформации, тело возвращается к исходной форме. В пределах упругости вещества сила и деформация пропорциональны друг другу.

В этом случае справедлив закон Гука: действующей на тело (пружину) силе противодействует упругая сила F = - cx.

Коэффициент пропорциональности равен коэффициенту упругости (жесткость).

Упругость означает существование однозначной монотонно возрастающей функции, связывающей напряжение s = F/S (S - площадь поперечного сечения) и деформацию ε = x/l (x – относительное перемещение концов, l – длина образца): s = Е ε, Е – модуль упругости.

Пример изменения формы тела – изменение длины пружины. Изменение формы тела (деформация) вызывается относительным смещением элементов (молекул). Деформации, исчезающие с прекращением действия силы – упругие деформации. В пределах упругости вещества силы и деформации пропорциональны друг другу. В этом случае справедлив закон Гука.

Потенциальная энергия включает энергию положения и энергию упругой деформации.

Действующей на тело (пружину) силе противодействует упругая сила F = - сs, где с – жесткость пружины (с = F / s).

Если пружина растягивается на длину s, то действующая на пружину сила возрастет пропорционально s от 0 до F_макс. Среднее значение силы равно 1/2 F_макс.

Работа, затрачиваемая на деформацию пружины A = F/2 s, но F = -с s, тогда А = cs²/2, где с - жесткость тела или пружины. Эта работа запасается в виде потенциальной энергии упругой деформации (растянутой пружины): W_п = cs²/2.

Закон Гука является примером линейной зависимости перемещения от растягивающей силы F = - сx. Нелинейными упругими свойствами обладают, например, высокоэластичные резиновые шнуры – ели такой шнур растянуть в десять раз (ε = 0,9), а затем отпустить, он восстановит свою длину. Если длинные металлические проволоки подвергать малым деформациям (ε = 0,001), нелинейность не обнаруживается. При растяжении металлического стержня по мере возрастания растягивающего напряжения s деформация ε сначала растет по линейному закону. Это означает, что при таких ε первый член разложения функции s = f (ε) (полагая ее аналитической) в степенной ряд s = ε ∂f /∂ε + ½! ε²∂²f /∂ε² + ... значительно превосходит все остальные. Тогда s = Еε (Е – модуль упругости материала при его одноосном сжатии). Нелинейный закон – параболическая зависимость s = Аε - Вε².

5.2 Уравнения движения

Одна из основных задач классической механики - задача прогнозирования движения различных тел и сред – решается на основе математической модели механического движения, которая представляет собой систему дифференциальных уравнений относительно координат и скоростей движущегося объекта. С помощью дифференциальных моделей решается большинство задач механики, гидродинамики, электродинамики и др.

Принцип независимости действия сил: если на материальную точку одновременно действует несколько сил, то каждая из них сообщает точке ускорение, определяемое 2-м законом Ньютона так, как если бы других сил не было, результирующее ускорение определяется действием результирующей силы.

Пример проекции сил.

Тело может находиться в равновесии, если сумма проекций приложенных к нему сил на любое направление равна нулю.

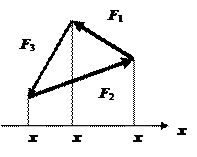F1x = x1 – x2, F2x = x2 – x3, F3х = x3 – x1. При равновесии сумма проекций сил равна нулю: F1x + F2x + F3х = 0.

Действие трех сил на тело. 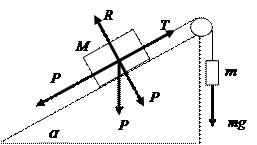        Действующие силы: тяжести P = Mg, натяжения нити Т = mg, реакции (ограничивают движение тела) R. P2 = Psinα = Mgsinα Равновесие обеспечивается при Т = Р2, R = Р1. Тогда условие равновесия: Mgsinα = mg, Msinα = m.

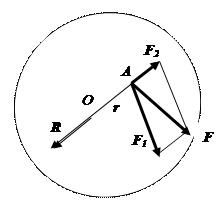Вращение тела вокруг жесткой оси. Если сила F не проходит через ось вращения – на тело действует сила вращения. Сила F₁, которая проходит через ось вращения тела уравновешивается силой реакции R = F₂. Вращение – только под действием силы F₁, перпендикулярной линии, проходящей через точку А приложения силы и ось вращения О.

Для равновесия тела, закрепленного на оси, существенен не сам модуль силы, а произведение модуля на расстояние (плечо) – момент силы относительно оси: M = F₁r. Если момент равен нулю – сила не вызывает вращения.

Согласно законам Ньютона все изменения состояния движения вызываются силами.

Уравнения движения определяют соотношения между скоростью, перемещением и временем.

Силу, как и любой вектор можно спроектировать на любую ось.

Уравнение движения материальной точки (системы точек) определяет связь ускорения w_i и силы F_i, называется дифференциальным уравнением движения точки, и записывается в соответствии со вторым законом Ньютона:

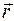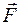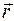m_id² / dt² = _i ( , d 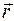/dt, t), i = 1,. . ., N,

где m_i - масса материальной точки, t > 0 – время, 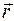- ее радиус-вектор, 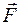_i - результирующая всех действующих на нее сил. Через 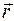обозначено множество координат всех точек системы. Величины 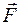_i считаются заданными и могут зависеть как от времени, так и от пространственных координат и скоростей всех рассматриваемых точек.

Величины 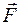_i считаются заданными и могут зависеть как от времени, так и от пространственных координат и скоростей всех рассматриваемых точек.

Силу, как и любой вектор, можно спроектировать на любую ось. Проекция вектора на ось равна разности координат начала и конца отрезка:

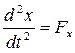m 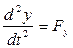, m , m .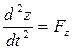

Различают два вида движения: поступательное и вращательное.

Динамика поступательного движения.

Основной закон поступательного движения: производная по времени от количества движения К материальной точки или системы точек относительно неподвижной (инерциальной) системы отсчета равна главному вектору всех сил, приложенных к системе: dK/dt = F, или mw_с = F, где w_с – ускорение центра инерции системы. К_i = m_i v_i

В прямоугольных декартовых координатах уравнение движения имеет вид:

dK_x/dt = F_х, dK_y/dt = F_y, dK_z/dt = F_z. m_i 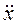= F_iх, m_i = F_iу, m_i 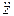= F_iz.

m dV_x/dt = F_х, m dV_y/dt = F_y

Простейшие случаи поступательного движения твердого тела.

а) Движение по инерции (F = 0) – равномерно поступательное движение (с постоянной скоростью):

mv = const, а = 0. v = const, S = vt.

б) Движение под действием постоянной силы – равномерно ускоренное движение (с постоянным ускорением):

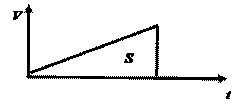
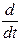(mv) = F = const, mv = Ft + mv₀, где mv - количество движения тела в начальный момент времени t = 0.

Время, за которое происходит изменение скорости из состояния покоя t=V/a

Из состояния покоя изменение скорости к моменту t: V=at Тогда S=vt/2 = at²/2

в) Неравномерно ускоренное движение

dS=Vdt 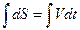S=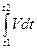

Тело брошено вертикально вверх с начальной скоростью v₀:

h_max = v₀²/2g.

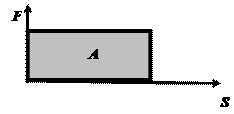Работа = Сила х Перемещение.

При F = const (в случае постоянной силы в процессе перемещения) A = F s, в случае переменной силы – интеграл от силы по перемещению A = .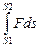

Если тело движется в направлении действия силы тяжести, то над телом совершается работа A = mg h.

Чтобы поднять тело (увеличить расстояние от центра Земли), над ним следует совершить работу. Работа, совершаемая силой F при движении против силы тяжести (подъеме тела) на высоту h не зависит от пути – зависит только от того, насколько тело может опуститься до заданного уровня. Эта работа запасается в виде потенциальной энергии тела (энергии положения) A =W_п = mgh, равной работе, затраченной на подъем тела.

Это не полная потенциальная энергия – только приращение энергии при подъеме тела на высоту (начало отсчета выбирается произвольно). С учетом изменения гравитационного поля по высоте

W_п = m .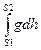

Потенциальной энергией называется энергия, зависящая только от взаимного расположения материальных точек (или тел). Во всех физических явлениях важна не сама потенциальная энергия, а ее изменение, которым определяется совершаемая работа. Уровень отсчета изменений заранее оговаривается.

При подъеме на высоту накопилась потенциальная энергия W_п, при падении с этой высоты эта потенциальная энергия превратилась в кинетическую W_к. W_п= W_к = mgh = mv²/2.

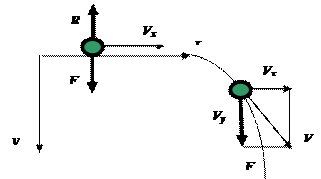Тело брошено горизонтально с начальной скоростью v₀ – комбинация двух движений взаимно перпендикулярных друг другу: горизонтального (равномерного прямолинейного) и вертикального (свободного падения).

Координаты каждой точки траектории:

- перемещение тела в горизонтальном направлении x = v₀ t;

- перемещение тела в вертикальном направлении (равномерно ускоренное движение с ускорением g) y = gt²/2.

Из этих уравнений движения: t = x / v₀ , y = gx² / 2v₀ – парабола.

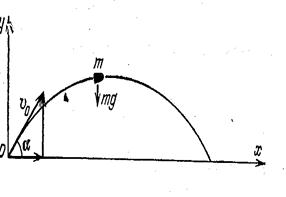
Тело, брошено под углом к горизонту.

Как и в случае горизонтально брошенного тела, тело движется, в результате комбинации двух движений: равномерного прямолинейного движения под углом к горизонту и свободного падения в вертикальном направлении (под действием только силы тяжести – без реакции опоры).

В двумерной постановке тело, брошенное под углом к горизонту, рассматривается как материальная точка, движущаяся под действием лишь одной силы - постоянной силы его веса Р, направленной вертикально вниз. Начало координат – в точке приложения силы, обеспечившей начальную скорость полета.

Тело массы m, брошенное под углом к горизонту, движется под действием постоянной силы веса Р = F_т, направленной вертикально вниз Р = mg.

Уравнения движения можно представить как в векторной, так и в координатной форме.

Для произвольной точки М (х,у) траектории тела:

mv = Р t + mv₀, или v = gt + v₀.

Проецируя векторные соотношения на оси координат, получим уравнения движения в координатной форме.

m dv_x /dt = 0, v_x = dx/dt,

m dv_y /dt = - mg, v_y = dy/dt

Необходимо найти зависимости x(t), y(t), v_x(t), v_y(t) из решения полученной системы дифференциальных уравнений при начальных условиях:

x(0) = x₀, y (0) = y₀, v_x (0) = v₀ cos Θ ₀, v_y (0) = v₀ sin Θ ₀.

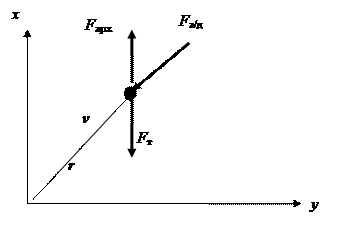
Сопротивление воздуха

Cила сопротивления воздуха F_а/д (полная аэродинамическая сила) направлена противоположно вектору скорости тела прямо пропорциональна величине скоростного потока q и характерной площади тела S:

F_а/д = - CrqS, q = ρv²/2,

где Cr - коэффициент сопротивления, зависящий от свойств среды и тела, скорости потока, ρ [кг/м³] – плотность воздуха, зависит от высоты.

Коэффициент сопротивления определяется опытным путем, и для приближенных расчетов для тела в форме шара может быть принят независимым от скорости потока и равным 0,25 (плюс – минус 0,05 – в зависимости от скорости).

Тогда система уравнений запишется в виде:

dv_x /dt = Cr qS cos Θ / m, v_x = dx/dt,

dv_y /dt = Cr qS sin Θ / m - g, v_y = dy/dt

ρ = ρ (y), α = arctg v_x / v_y, q = ρv²/2

при начальных условиях:

x (0) = x₀, y (0) = y₀,

v_x (0) = v₀ cos Θ ₀, v_y (0) = v₀ sin Θ ₀.

Зависимость ρ = ρ (y) может быть задана в табличном или в аналитическом виде.

Задача не имеет аналитического решения и решается численным интегрированием. Определяется влияние шага интегрирования на точность решения задачи.

Изменение с высотой величины ускорения силы тяжести Земли

Ускорение свободного падения одинаково для всех тел и, также как и вес, зависит от географической широты и высоты над уровнем моря.

Стандартное (нормальное) значение ускорения свободного падения на уровне моря составляет g0 = 9,81 м/сек². Для определения ускорения при удалении от поверхности Земли на высоту h используется формула g = g₀[R₀/(R₀ + h)]², R₀ = 6370 км - радиус Земли. На географических полюсах (φ = 900) Fц = 0 и вес тела равен силе притяжения его к Земле. Вследствие того, что центростремительная сила зависит от широты, вес тела максимален на полюсах и минимален на экваторе, различие не превышает 0,55%.

Величина выталкивающей силы (закон Архимеда)

На тело действует выталкивающая сила воды в соответствии с законом Архимеда.

По закону Архимеда выталкивающая сила равна F_арх = g(y)Vρ₀(y). Здесь Vρ₀(y) – масса вытесненного воздуха, V – объем тела.

Величины присоединенной массы

Присоединенная масса может быть определена по формуле: m = 0,5 Vρ₀.

Изменения плотности атмосферы с высотой

Гипотеза о постоянстве плотности атмосферы (ρ₀ = 1,225 кг/м³) с высотой полета изменяется ρ = ρ (h), где h – высота над уровнем моря [м]: ρ = ρ₀^{- 0, 00014h}.

Кривизны Земли

Для учета кривизны Земли необходимо строить новую математическую модель - начало системы координат помещается в центр Земли. В этом случае сила притяжения направлена в начало координат (а не перпендикулярно оси координат), и тип кривой полета становится другим (эллипс, а не парабола).

Дата добавления: 2014-08-04; просмотров: 602; Нарушение авторских прав

Мы поможем в написании ваших работ!