Движение тела переменной массы

Дифференциальное уравнение поступательного движения твердого тела, масса которого зависит от времени, имеет вид

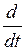(mv) = F + v₁ 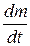, где F – главный вектор всех сил, действующих на тело, v₁ – скорость присоединяющейся массы до присоединения (если dm/dt > 0) или скорость отделяющейся массы после отделения (если dm/dt < 0).

Ускорение w тела переменной массы w = 1/m(F + F_p), где F_p = (v₁ – v)dm/dt = udm/dt – реактивная сила, равная произведению производной по времени от массы тела на относительную скорость u = v₁ – v присоединяющейся или отделяющейся массы.

Пример. Движение ракеты в условиях отсутствия внешнего силового воздействия.

Реактивная сила, создаваемая двигателем, - сила тяги ракеты: F_p = u dm/dt, где dm/dt - скорость уменьшения массы ракеты за счет выгорания топлива.

Уравнение движения ракеты: m dv/dt = u dm/dt,

где v и m - скорость и масса ракеты в произвольный момент времени t, u - относительная скорость отделяющейся массы.

Векторы dv/dt и u направлены в противоположные стороны, потому m dv/dt = - u dm/dt, откуда при u = const следует уравнение Циолковского: v = v₀ + ulnm₀/m, где v₀ и m₀ - начальные значения скорости и массы ракеты (при t =0).

5.3 Уравнения состояния

Состояние тела определяется его внутренней энергией.

Термодинамическая система

Термодинамической системой называется совокупность макроскопических объектов (тел и полей), обменивающихся энергией в форме работы и в форме теплоты как друг с другом, так и с внешней средой (внешними по отношению к системе телами и полями).

Состояние термодинамической системы определяется совокупностью значений ее термодинамических параметров (параметров состояния) – всех физических величин, характеризующих макроскопические свойства системы (плотность, энергию, вязкость, поляризацию, намагниченность и т.д.). Основные термодинамические параметры состояния – давление, температура и удельный объем.

Всякое изменение состояния термодинамической системы называется термодинамическим процессом. Изопроцессы – термодинамические процессы, протекающие при неизменном значении какого-либо параметра состояния. Состояние системы называется стационарным, если оно не изменяется во времени.

Термодинамический метод состоит в изучении свойств системы взаимодействующих тел путем анализа условий и количественных соотношений происходящих в системе превращений энергии.

Энергия системы, зависящая только от ее термодинамического состояния, называется внутренней энергией. Если система не подвержена действию внешних сил и находится в состоянии макроскопического покоя, внутренняя энергия системы является ее полной энергией.

Внутренняя энергия системы включает в себя энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов и др.), энергию взаимодействия этих частиц, энергию электронных оболочек атомов и ионов, внутриядерную энергию и т.д.

Температура тела характеризует энергию, с которой движутся его молекулы, и характеризует состояние тела (является параметром состояния).

Внутренняя энергия является функцией состояния системы, т.е. зависит только от параметров состояния p, V , T и не зависит от способа, которым это состояние достигнуто.

Каждому термодинамическому состоянию системы соответствует определенное значение внутренней энергии.

Первый закон термодинамики: тепловая энергия, подведенная к замкнутой системе, расходуется на повышение ее внутренней энергии и работу, производимую системой против внешних сил.

Тепловая энергия (количество теплоты) представляет собой один из видов энергии и подчиняется закону сохранения энергии. Тепловая энергия может возникать в результате превращения других видов энергии (механической, электрической, химической и др.).

При нагревании амплитуда колебаний молекул увеличивается, расстояние между ними возрастает, и тело занимает больший объем.

Для твердого тела объемное расширение можно рассматривать как линейное расширение в трех направлениях.

В жидкостях при нагревании изменяется не только объем, но и плотность жидкости. Объем изменяется в соответствии с коэффициентом объемного расширения β: V₂= V₁(1 + β∆t). Объем и плотность жидкости обратно пропорциональны друг другу: ρ₁/ ρ₂ = V₂/V₁, тогда ρ₂ = ρ₁ / (1 + β∆t).

Газы расширяются значительно сильнее, чем твердые и жидкие тела. При постоянном давлении объем газа пропорционален абсолютной температуре, при постоянном объеме давление газа пропорционально абсолютной температуре (законы Гей-Люссака). Уравнение состояния идеального газа: pV = mRT (R – газовая постоянная). Газ считается идеальным, если для него при постоянной температуре выполняется равенство pV = const (закон Бойля-Мариотта). В реальних газах (вблизи токи конденсации – при высоком давлении и низкой температуре) свойства газа значительно отличается от идеального.

Твердые тела, жидкости и газы

Упругие свойства твердых тел

Ранее рассматривалось тело как материальная точка и абсолютно твердое тело. На самом деле внешние силы изменяют форму и объем реального тела – деформируют его. При деформации происходит относительное смещение элементов тела (его молекул). Деформации, исчезающие с прекращением действия силы, называются упругими. При превышении предела упругости в кристаллических решетках возникают необратимые изменения – происходит пластическая деформация тела. Тело не возвращается к исходной форме даже после прекращения действия внешних сил.

Внешние силы могут вызывать различные изменения тела – растяжение, сжатие, сдвиг.

Сила растяжения или сжатия, приложенная к стержню вызывает изменение длины тела - ∆x. Величина ∆x зависит от размеров стержня, материала, величины самой силы.

Закон Гука связывает линейную связи деформацию и механическое напряжение в упругом материале (упругие деформации прямо пропорциональны вызвавшим их воздействиям F = - kx).

Напряжение (σ = F/S, где F - сила, S – площадь поперечного сечения стержня) пропорционально поперечному сечению: σ = Еε, где Е – модуль упругости.

Механическое напряжение в продольном направлении кроме удлинения вызывают поперечное сжатие тела – с изменением длины тела изменяется и его поперечное сечение.

Относительное изменение поперечного размера тела ε_п = - με, где μ – коэффициент Пуассона.

Если к параллельным плоскостям тела приложены параллельные силы, направленные в разные стороны, то эти плоскости смещаются относительно друг друга. Такая деформация характеризуется углом сдвига. По аналогии с законом Гука, касательное напряжение τ = Gγ, G где – модуль сдвига, γ - сдвиговая деформация (угол сдвига).

Жидкости

Жидкостями называются тела, которые имеют определенный объем, но не имеют упругости формы (отсутствие модуля сдвига). Жидкости отличаются сильным межмолекулярным взаимодействием и вследствие этого малой сжимаемостью. Вследствие подвижности молекул жидкость не обладает собственной формой, а принимает форму сосуда, поверхность жидкости всегда перпендикулярна действующей на жидкость силе.

Если на жидкость действует внешнее давление, то вследствие подвижности молекул это давление передается одинаково во все стороны.

Закон Архимеда. На погруженное в жидкость тело действует подъемная выталкивающая сила, направленная вверх и равная весу вытесненной телом жидкости: F = gVρ₀, где V – объем тела, ρ₀ - плотность жидкости.

Газы

Молекулы газа практически не взаимодействуют друг с другом - в идеальным газе отсутствуют силы межмолекулярного взаимодействия (состояния, далекие от областей фазовых превращений). Поэтому газы не имеют формы и объема и целиком заполняют сосуд, в котором находятся.

Часто под внутренней энергией понимают только те ее составляющие, которые изменяются в рассматриваемых процессах. Например, при не слишком высоких температурах внутреннюю энергию идеального газа можно считать равной сумме кинетических энергий хаотического движения его молекул (тепловая энергия). Внутренняя энергия идеального газа зависит только от его абсолютной температуры и пропорциональна массе газа.

Для идеальных газов справедливы следующие законы.

Уравнение Клайперона-Менделеева (уравнение состояния идеального газа) о связи давления с плотностью и температурой: pV = RT, где p - давление, V_μ – молекулярный объем (объем, который занимает грамм-молекула), T – температура, R - газовая постоянная. Для произвольной массы М объем V = V_μ М/μ.

Закон Бойля-Мариотта: pV = const - при неизменной температуре и массе.

Закон Гей-Люссака: V = V₀ T/T₀ – при постоянном давлении объем данной массы газа прямо пропорционален его абсолютной температуре.

Закон Шарля: р = р₀ T/T₀ – при постоянном объеме давление данной массы газа прямо пропорционален его абсолютной температуре.

Закон Фурье: q_t = - λ dT/dx – о связи плотности теплового потока и градиента температуры.

6 УНИВЕРСАЛЬНОСТЬ МОДЕЛЕЙ

Система может быть представлена в виде совокупности различных физически однородных подсистем, математическая модель каждой из которых описывает элементарные явления и процессы определенной физической природы (механические, гидравлические, тепловые, электрические) в основном в виде дифференциальных уравнений.

Большинство инженерных дисциплин можно рассматривать как упорядоченное множество математических моделей и расчетных схем – по существу, сложились базы данных математических моделей типовых элементов и расчетных схем.

6.1Типовые математические модели элементов и подсистем

Большинство технических систем при всем их разнообразии обычно можно разделить на блоки, узлы, элементы, процессы в которых могут быть описаны функциональной математической моделью, отражающей физические, механические, химические, информационные процессы. Для каждого из таких процессов можно выделить типовые элементы, каждый из таких элементов можно рассматривать как электрическую, механическую поступательную или вращательную, тепловую, гидравлическую или пневматическую систему и представить математической моделью микроуровня.

В общем случае эти системы взаимосвязаны, но, используя принцип декомпозиции, их можно представить совокупностью простейших типовых элементов, и описывать систему моделями макроуровня.

Наиболее часто используются типовые элементы, описывающие колебательные процессы, электрические, гидравлические, пневматические, тепловые процессы.

При построении моделей типовых элементов удобно исследовать причины неадекватности моделей. Для выявления области адекватности модели иногда требуется рассмотрение модели микроуровня физических процессов в типовых элементах – обоснование области применения модели того или иного типа (линейной – нелинейной, статической – динамической и т.п.).

Типовые элементы являются идеализированными по отношению к реальным элементам технических систем – применение математических типовых элементов макроуровня вызывает неизбежные погрешности. Для оценки адекватности модели необходима хотя бы грубая оценка таких погрешностей – количественный анализ уточненной модели микроуровня физических процессов, учитывающей свойства и эффекты, которые не были учтены в матмоделях типовых элементов. Одной из причин возникновения пошрешностей является пренебрежение пространственным распределением параметров, характеризующих свойства типовых элементов и протекающие в них процессы.

Модель колебательного процесса

Колебаниями или колебательным движением называется движение (изменение состояния), обладающее повторяемостью во времени - процесс изменения параметров системы с многократным чередованием их возрастания и убывания.

Колебания по своей физической природе весьма разнообразны (механические, электромагнитные колебания и др.).

Осциллятор - система, в которой какие-либо параметры совершают колебания при отсутствии переменных внешних воздействий.

При колебаниях происходит знакопеременное отклонение параметров от их определенных значений. Эти значения могут соответствовать установившемуся состоянию системы или изменяться во времени по некоторому закону. Как привило, колебания сопровождает преобразование одной формы энергии в другую.

Любые колебания представляют собой движение с переменным ускорением, отклонение (мгновенное перемещение относительно положения равновесия), скорость и ускорение являются функциями времени. Для любых колебаний характерна периодичность.

Маятник может не только колебаться со своей собственной частотой, его можно заставить колебаться под влиянием внешнего воздействия. Если это влияние периодическое, оно может навязать осциллятору свою частоту. Наличие маятника собственной частоты проявляется в явлении резонанса. Малое воздействие частоты, близкой к частоте маятника (резонансной частоты) может привести к сильным колебаниям, тогда как на далекое от собственной частоты воздействие маятник может реагировать слабо.

Общее представление об осцилляторе как колебательной системе, описываемой простым дифференциальным уравнением, стало основой общей для многочисленных конкретных случаев математической модели. Наука о колебаниях легла в основу радиотехники, радиофизики, прикладной и теоретической механики. В поведении осциллятора находят многие разнообразные явления. Одна из универсальных моделей – осциллятор механический, электрический. Механический маятник - в основе часов. Колебательный контур электрического маятника, состоящий из самоиндукции и емкости – в основе радиопередатчика и радиоприемника.

Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.

Период колебаний Т – наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебательное движение.

Отклонение х = f (t) – мгновенное перемещение относительно положения равновесия.

Амплитуда – А – максимальное абсолютное значение отклонения - максимальное отклонение Х_max, размах колебаний.

Частота колебаний n – число полных колебаний в единицу времени n = 1/Т (измеряется в герцах). Угловая частота w = 2p n = 2p / Т.

Фаза j = w t + j₀. Характеризует мгновенное состояние колебательной системы и определяется двумя параметрами (отклонением и временем).

Зависимость от времени t, периодически колеблющейся физической величины S имеет вид:

S = S₀ + х(t), где S₀ – значение величины S в положении равновесия, х(t) – периодическая функция времени: х(t + T) = х(t).

Простейший тип периодических колебаний являются гармонические (синусоидальные) колебания:

х = A sinj = A sin(w t + j₀) или x = A cos(w t + j₁), где A,w, j₀, j₁ - постоянные величины, причем А > 0, w > 0, j₁ = j₀ + p/2. А – максимальное абсолютное значение х – амплитуда колебания.

Первая и вторая производная по времени от гармонически колеблющейся величины y также изменяется по гармоническому закону:

х’ = Aw cos(w t + j₀) = A w sin(w t + j₀ + p /2),

х’’ = - Aw² sin (w t + j₀) = Aw² sin(w t + j₀ + p) = - w²х.

Следовательно, гармонически колеблющаяся величина х удовлетворяет уравнению (дифференциальное уравнение гармонических колебаний): х’’ + w²х = 0.

Это же соотношение получается и из геометрического построения, поскольку гармонические колебания можно рассматривать как проекцию равномерного движения по окружности.

Гармонические колебания представляют собой движение с переменным ускорением – ускорение является функцией времени.

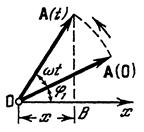Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды.

Вектор А, численно равный амплитуде колебаний, равномерно вращается против часовой стрелки вокруг оси О, перпендикулярной плоскости чертежа, с угловой скоростью w. Если в момент времени t = 0 угол между вектором А и осью Ох равен j₁, то проекция В конца этого вектора на ось Ох совершает гармонические колебания по закону x = A cos(w t + j₁).

Свободные колебания – колебания, которые возникают в системе, не подверженной действию внешних сил, в результате какого-либо начального отклонения этой системы от состояния начального равновесия.

При любых колебаниях отклонение системы вызывает появление восстанавливающей силы, которая стремится возвратить систему в положение равновесия. Линейный закон силы: восстанавливающая сила пропорциональна ускорению. Согласно основному закону динамики F = ma

При отклонении точки от положения равновесия потенциальная энергия возрастает, если после отклонения точка начнет движение, то при отсутствии сопротивления в силу закона сохранения энергии (кинетическая и потенциальная энергии системы равны) точка будет совершать незатухающие колебания относительно положения равновесия.

Движение шарика, присоединенного к пружине.

Рассмотрим модель движения шарика, присоединенного к пружине с жестко закрепленным концом.

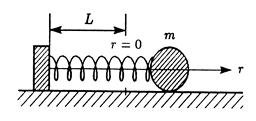Пусть r – координата шарика вдоль оси пружины, лежащей на горизонтальной плоскости. и направление движения шарика совпадает с ее осью. Тогда по второму закону динамики

F = ma = md²r/dt²,

где m – масса шарика, а – его ускорение. Будем считать плоскость идеально гладкой (движение происходит без трения), пренебрежем сопротивлением воздуха и примем во внимание то, вес шарика уравновешивается реакцией плоскости.

Единственная сила, действующая на шарик в направлении оси r, очевидно, сила упругости пружины. Определим ее, используя закон Гука, гласящий, что для растяжения (сжатия) пружины необходимо приложить силу

F = - kr,

Где коэффициент k > 0 характеризует упругие свойства пружины, а r – величину ее растяжения или сжатия относительно нейтрального, ненагруженного положения r = 0. Уравнение шарика принимает вид (уравнение элементарного осциллятора)

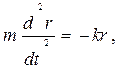t > 0. (1)

Оно описывает его гармонические колебания и имеет общее решение

r(t) = r₀ /ω sinωt + r₀ cos ωt r = A cos (ωt+φ), (2)

где 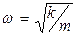- частота колебаний пружины в отсутствии внешних сил или собственная частота колебаний системы "пружина – шарик", не зависящая от начальных условий и определяющая период Т = 2π/ω колебаний, измеряемый в секундах, 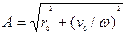- амплитуда колебаний, φ = arctg(ω r₀ / v₀). В отличие от угловой частоты, измеряемой в рад/с, частота колебаний f = 2πω измеряется в герцах.

Значения коэффициентов определяются из начального состояния объекта, т.е. через величины r(t = 0) = r₀ и v(t = 0) = v₀ (v(t) - скорость шарика), причем r(t) ≡ 0 при r₀ = v₀ = 0.

Уточнение модели.

1. Пусть на шарик действует известная внешняя сила F (r, t), зависящая от времени и положения шарика. Она может порождаться полем тяготения, иметь электрическое или магнитное происхождение и т.д.

По сравнению с базовой моделью колебаний в правой части уравнения появляется дополнительный член – внешняя сила

md²r/dt² = - kr + F (r, t).

Примем, что внешняя сила F постоянна F (r, t) = F₀. Проводя замену r* = r - F₀ / k, получаем для r*

d²r*/dt² = - kr*,

т.е. постоянная сила не вносит изменений в процесс колебаний за тем исключением, что координата нейтральной точки, в которой сила, действующая на шарик равна нулю, сдвигается на величину F₀ / k.

2. Рассмотрим случай, когда внешняя сила зависит от времени, для определенности примем эту зависимость периодической F (t) = F₀ sinω₁t:

md²r/dt² = - kr + F (t) = - kr + F₀(t) = - kr + F₀ sinω₁t. (3)

Решение этого уравнения будем искать как сумму общего решения однородного уравнения (2) и частного решения неоднородного уравнения (3) в виде r₁(t) = C sinω₁t. Подстановкой этого выражения в (3) находим

С = F₀ / (k - m ω₁²) = F₀ / m (ω₁² - ω₁²),

В итоге для общего решения системы (3) имеем

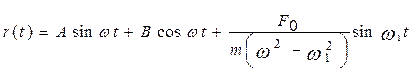
Внешняя сила F (t) приводит не только к появлению в системе дополнительных колебаний с частотой ω₁, но и к возникновению резонанса – неограниченному росту амплитуды колебаний при ω₁ → ω.

Учет силы трения (пример неконсервативной системы).

Силы трения могут появиться по двум причинам: неидеальность поверхностей движения и сопротивление среды (воздуха, воды и т.п.).

В первом случае внешняя сила (сила трения) постоянна - пропорциональна весу и площади соприкосновения, не зависит от скорости и направлена против движения шарика (ее знак противоположен знаку скорости шарика).

В связи с наличием того или иного вида трения (механическая энергия с течением времени уменьшается за счет преобразования в другие виды энергии, например, в теплоту) происходит рассеяние (диссипация) энергии. В некоторых случаях рассеяние может быть настолько медленным, что им можно пренебречь при исследовании поведения системы для непродолжительного промежутка времени. Системы такого типа называются консервативными.

Механическая энергия консервативной системы (отсутствие рассеяния энергии) сохраняется неизменной в процессе движения системы: имеет место закон сохранения механической энергии - сумма кинетической и потенциальной энергий постоянна в процессе движения системы. Закон справедлив для любой замкнутой системы тел, силы взаимодействия между которыми потенциальны. Если эти силы непотенциальны (например, есть силы трения), то механическая энергия замкнутой системы уменьшается.

Сила трения равна F = k₁P, где – k₁ коэффициент трения (на единицу поверхности), P = mg – вес шарика. Движение шарика подчиняется уравнению md²r/dt² = - kr – k₁mg sign dr/dt.

Оно внешне похоже на уравнение с постоянной силой F₀, но из-за знакопеременности не сводится к стандартному уравнению колебаний – эти уравнения описывают существенно разные процессы. В частности, амплитуда колебаний шарика существенно уменьшается со временем.

Во втором случае внешняя сила (сила трения) не постоянна - существенно зависит от скорости движения F = - μv, где коэффициент μ > 0 определяется размерами шарика, плотностью среды, ее вязкостью.

При малой вязкости в системе происходят затухающие со временем колебания, при большой вязкости колебания отсутствуют благодаря подавляющему действию сил вязкого трения.

Электрическая подсистема

Электрическая модель является наиболее и универсальной для описания явлений и процессов различной природы.

Типовыми простейшими элементами электрической подсистемы являются резистор с электрическим сопротивлением R, конденсатор без потерь заряда с электрической емкостью C, индуктивная катушка без сопротивления с электрической индуктивностью L.

При описании их функционирования используются переменные: сила тока I, напряжение U. Значение напряжения на элементах совпадает с разностью значений электрического потенциала на концах элементов, напряжение на элементе источника тока равно его ЭДС (электродвижущей силе).

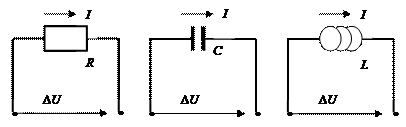ΔU = IR I = С dΔU /dt ΔU = L dI /dt.

Резистор является характерным представителем типового элемента, обладающего свойством оказывать сопротивление переносу некоторой физической субстанции (в данном случае электрических зарядов).

Электрический заряд – произведение силы тока I на время протекания тока: q=It, или I= q/t. Для прохождения через такой элемент физического потока необходимо располагать разностью потенциалов на входе в элемент и на выходе из него.

Математическая модель резистора, описывающая протекание через него электрического тока представляет собой алгебраическое уравнение – закон Ома ΔU = IR,

где ΔU – падение электрического напряжения на резисторе (разность электрических потенциалов), I – сила тока.

Электрический конденсатор обладает свойством накапливать электрический заряд пропорционально разности потенциалов ΔU на его обкладках. Энергия электрического поля в конденсаторе равна Е = С (ΔU )²/2.

По физическому смыслу емкости конденсатора С (емкость равна величине заряда, который необходимо помесить на обкладки конденсатора для увеличения разности потенциала между ними на единицу С = q/u) в любой момент времени имеем равенство U_C = q(t)/С.

Для конденсатора с постоянной емкостью С при изменении ΔU в цепи во времени протекает ток силой I. Математическая модель конденсатора представляет собой обыкновенное дифференциальное уравнение 1-го порядка I = С dΔU /dt.

Индуктивная катушка обладает свойством инерции, проявляющимся в стремлении сохранить поток субстанции неизменным.

При изменении во времени силы тока, протекающего через индуктивную катушку, возникает электродвижущая сила самоиндукции, препятствующая изменению силы тока. Эту ЭДС можно представить как разность потенциалов на концах катушки. Математическая модель индуктивной катушки представляет собой обыкновенное дифференциальное уравнение 1-го порядка

U_L = L dI/dt.

Очевидно, что ток i(t) и напряжение u(t) также являются функциями времени. Производная заряда по времени dq/dt определяет мгновенное значение тока через катушку индуктивности L.

Среди простейших типовых элементов, в которых протекают процессы иной физической природы по сравнению с электрической системой, можно выделить элементы со свойствами, аналогичными свойствам резистора, конденсатора, индуктивной катушки.

Резистор является характерным представителем типового элемента, обладающего свойством оказывать сопротивление переносу некоторой физической субстанции (в данном случае электрических зарядов). Для прохождения через такой элемент физического потока необходимо располагать разностью потенциалов на входе в элемент и на выходе из него.

Конденсатор обладает свойством накапливать эту субстанцию при повышении разности потенциалов. Энергия электрического поля в конденсаторе равна Е = С (ΔU )²/2.

Индуктивная катушка обладает свойством инерции, проявляющимся в стремлении сохранить поток субстанции неизменным.

Элементы электрической схемы объединяются в систему с помощью уравнений равновесия и непрерывности (первый и второй законы Кирхгофа), устанавливающие равенство нулю суммы токов в узлах схемы и суммы напряжений в элементах схемы при их обходе по произвольному контуру:

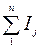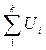= 0; = 0,

где n – число ветвей в узлах схемы, к – число элементов в контуре схемы.

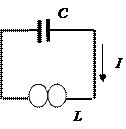
Колебательный электрический контур.

При электромагнитных колебаниях периодически колеблются энергии электрического и магнитного полей.

Электромагнитные колебания возникают в колебательном контуре, состоящем из электрического конденсатора емкостью С и индуктивной катушки индуктивностью L (электрическое сопротивление отсутствует).

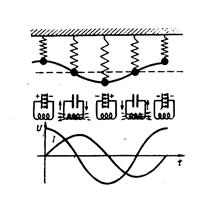Если конденсатору сообщить заряд, то разность потенциалов ΔU, существующая на конденсаторе, подается непосредственно на катушку (считаем, что сопротивление отсутствует) – конденсатор будет разряжаться через катушку индуктивности. Ток разрядки создает магнитное поле, которое в свою очередь обеспечит заряд конденсатора, имеющий противоположную полярность. Сила тока и напряжение будут изменяться во времени по периодическому закону. При отсутствии сопротивлений колебания не затухают.

На рисунке приведена аналогия между механическими и электромагнитными колебаниями.

Для вывода уравнений электромагнитных колебаний целесообразно рассматривать колебания заряда q, мгновенное значение которого на конденсаторе с емкостью С определяет мгновенное напряжение u_С. Необходимо получить уравнение для изменяющейся со временем величины заряда на обкладках конденсатора q(t).

В каждый момент времени напряжения на катушке и конденсаторе должны быть равны друг другу:

U_С + U_L = 0, где U_C = q/С, U_L = L di/dt = L d²q/dt².

Отсюда следует L d²q/dt² + q/С = 0,

После деления на L получаем дифференциальное уравнение незатухающих электромагнитных колебаний d²q/dt² + q/(L С) = 0.

Модели элементов гидравлических систем

Технические системы, в которых происходит перемещение несжимаемой жидкости, принято называть гидравлическими. Зарубин стр. 110

Участок трубопровода.

По аналогии с электрическими системами: разности электрических потенциалов (напряжений) соответствует разность (перепад) давлений ∆р в гидравлической системе, силе тока в электрической системе соответствует объемный расход жидкости Q_ж, измеряемые соответственно в паскалях и м³/с.Рис.3.16 стр.110

Постоянный расход идеальной жидкости. Для участка достаточно длинного трубопровода с круглым поперечным сечением радиуса R при установившемся ламинарном течении вязкой жидкости справедлива следующая зависимость скорости v_z вдоль оси трубопровода от радиальной координаты r:

v_z = ∆р (R² - r²)/4ηl,

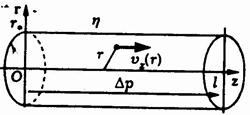где η – коэффициент сдвиговой вязкости жидкости, ∆р > 0 - перепад давления на участке трубопровода длиной l.

Объемный расход жидкости через трубопровод

Q_ж = 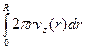= π∆р/2ηl 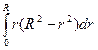= ∆ р π R⁴/8ηl.

Величину 8ηl/πR⁴ можно рассматривать как гидравлическое сопротивление R_г = 8ηl/πR⁴ участка трубопровода длиной l. Тогда ∆ р = Q_ж R_г– аналог закона Ома ∆U = IR.

Уточнение модели: если поперечное сечение трубопровода не круглое, то гидравлическое сопротивление R_r будет зависеть от формы сечения, при увеличении объемного расхода жидкости через трубопровод (скорости потока) ламинарный режим течения переходит в турбулентный, и в этом случае гидравлическое сопротивление становится функцией Q_ж – математическая модель оказывается нелинейной.

Математические модели простейших элементов гидравлических и электрических подсистем совпадают. Комбинируя элементами гидравлических систем, как и в случае электрических систем, можно учесть, например, влияние вязкости жидкости.

Применение электрогидравлической аналогии дает возможность для получения матмодели гидравлической системы применять детально разработанные и формализованные приемы построения электрических цепей.

Цилиндрический сосуд.

Рассмотрим цилиндрический сосуд с площадью поперечного сечения S, заполняемый и опорожняемый через трубопровод в нижнем плоском днище.

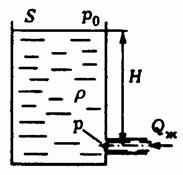Статическое давление на входе в трубопровод равно p = p₀ + rgH, где p₀ – давление над зеркалом жидкости, H - высота уровня жидкости. Рис.3.17 стр. 111 Зарубин

Скорость течения v будем считать достаточно малой, так что динамическим давлением rv²/2, где – плотность жидкости, можно пренебречь по сравнению со статическим давлением на входе трубопровода в сосуд.

Изменения во времени уровня жидкостии разности давлений ∆ р = р - p₀ связаны между собой зависимостью d∆р/dt = rg dH/dt. Тогда для объемного расхода жидкости через трубопровод:

Q_ж= S dH/dt = S/rg d∆р /dt = C_Г d∆р /dt,

где C_Г = S/rg - величина, аналогичная емкости С электрического конденсатора.

Нелинейность модели.

При заполнении жидкостью сосуда с переменной по высоте площадью поперечного сечения (сфера) величина C_Г будет зависеть от высоты уровня жидкости относительно трубопровода. Объем жидкости, заполняющей сосуд V_ж = 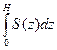, где S(z) – зависимость площади поперечного сечения сосуда от вертикальной координаты z, отсчитываемой от входа трубопровода. Так как объемный расход Q_ж= d V_ж /dt, то получаем нелинейное соотношение

Q_ж= S(H) dH/dt = S(H)/rg d∆р /dt .

Рассмотренные гидравлические модели являются квазистационарными – при их построении предполагалось, что возмущения, вызванные изменением давления или объемного расхода жидкости в трубопроводе, распространяются вдоль трубопровода мгновенно.

В действительности реальные жидкости обладают некоторой сжимаемостью – это приводит к тому, что возмущения распространяются с большой, но конечной скоростью v (скорость звука в жидкости). Если по длине трубопровода наименьшая длительность t_min протекающих в нем процессов удовлетворяет условию t_min>> l/v, то применение квазистационарных моделей не приводит к большим погрешностям. При нарушении этого условия модели становятся неадекватными реальному элементу. Например, они не применимы при моделировании процесса перекрытия трубопровода за время, одного порядка со значением, когда объемный расход жидкости быстро падает до нуля, что приводит к значительному повышению давления – гидравлическому удару.

Модели элементов пневматических систем

Под пневматическими понимают технические системы, в которых рабочей средой является воздух или газ. Рабочая среда, в отличие от газа является сжимаемой: ее плотность r существенно зависит от давления р.

Газ называют совершенным, если для него справедливо уравнение Клайперона-Менделеева p = rRT, где T – температура газа, R - удельная газовая постоянная для данного газа. Тогда r = p/RT, масса m = rV = pV/RT.

В пневматической системе, как и в гидравлической, величиной, имеющей смысл потенциала, является разность (перепад) ∆р давлений. В качестве величины, характеризующей перенос рабочей среды, вместо объемного расхода рассматривается расход массы газа dm/dt.

При установившемся ламинарном течении по трубопроводу вязкого газа с постоянным расходом m' = ∆р V/RT или ∆р = m'R_п, R_п = const. Это линейное соотношение аналогично закону Ома ∆U = IR.

Для сосуда с фиксированным объемом V, газ выпускается (температура и плотность считаются постоянными) - масса газа изменяется во времени t. Тогда при T = T₀ получим соотношение

m' = dm/dt = V/RT₀ dp/dt = m₀/p₀ dp/dt = C_пdp/dt.

Это выражение аналогично выражению для электрического конденсатора I = Cd∆U /dt (C – емкость конденсатора).

Для участка трубопровода длиной l и площадью поперечного сечения S для идеального (невязкого) газа, движущегося с изменяющейся во времени скоростью v(t), в соответствии со вторым законом Ньютона (F = ma): S∆р = r S l dv(t)/dt или ∆р = L_пdm'/dt, что аналогично выражению для ЭДС идеализированной (без сопротивления) катушки: ∆U = LdI/dt (L – индуктивность катушки).

Соотношение ∆р = m'R_п можно считать справедливым при условии, что изменение давления по длине трубопровода вызывает пренебрежимо малое изменение плотности r газа. Тогда можно принять r= const, что означает постоянство объемного расхода газа V' = m'/r. Если трубопровод имеет круглое поперечное сечение радиуса r_*, то можно использовать выражение для гидравлического сопротивления при ламинарном течении вязкой несжимаемой жидкости R_г = 8ηl/π r_*⁴. В этом случае R_п = R_г/r.

В достаточно длинном трубопроводе изменение давления газа может оказаться существенным, что вызовет заметное изменение плотности газа. В этом случае при постоянном расходе массы m' газа по длине трубопровода его объемный расход V' по длине трубопровода будет переменным. По длине трубопровода может также меняться температура – тогда будет изменяться и плотность газа.

Как и в случае несжимаемой жидкости, при турбулентном режиме течения газа зависимость сопротивления трубопровода от расхода газа становится нелинейной.

6.2 Модели на основе аналогий

Способ построения моделей с применением аналогий с уже изученными явлениями основан на предположении об универсальности моделей, т.е. приложимости их к объектам принципиально различной природы.

Например, предположение «скорость изменения величины пропорционально значению самой величины» широко используется в далеких друг от друга областях знаний.

У мaтемaтически подобных объектов процессы облaдaют различной физической природой, но описываются идентичными уравнениями.

Имеется ряд общих математически подобных моделей в физике, химии, биологии, экономике.

В простейших случаях используются известные аналогии между механическими, электрическими, тепловыми и другими явлениями.

Типичными для практического применения являются модели в виде наборов формул, систем линейных и нелинейных алгебраических и дифференциальных уравнений, дискретных переходов, статистических описаний, описании игровых ситуаций и т.д.

У мaтемaтически подобных объектов процессы облaдaют рaзличной физической природой, но описывaются идентичными урaвнениями.

Примеры различных по физической природе явлений и их мaтемaтические описания: в законах Фурье, Ньютона, Ома нaблюдaется подобие мaтемaтических описaний различных физических явлений. Поэтому любой из этих процессов с использовaнием определенных пересчетных коэффициентов может служить моделью другого процесса. Закон Ньютона притяжения двух материальных точек и закон Кулона взаимодействия двух точечных электрических зарядов при соответствующем выборе единиц измерения физических величин можно выразить одинаковыми формулами.

Закон Фурье: q_t = - λ dT/dx Закон Ньютона: F = dK/dt

Закон Ньютона: 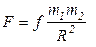Закон Кулона: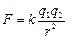

Как видно, нaблюдaется подобие мaтемaтических описaний рaзличных физических явлений. Поэтому любой из перечисленных процессов может служить моделью другого.

Пример универсальности моделей – электрические схемы, процессы колебаний различной природы – несмотря на разную сущность объектов, им соответствуют одни и те же модели.

Воспроизводится не сам физический процесс, а его мaтемaтическое описание или аналогия между законами, которые одинаково выражают явление и в оригинале, и в модели. Процесс изучается на модели, в которой протекает другой по своей природе процесс, если мaтемaтические описaния этих процессов изоморфны (все свойства модели соответствуют свойствам оригинала).

Дата добавления: 2014-08-04; просмотров: 1751; Нарушение авторских прав

Мы поможем в написании ваших работ!