Перевозка неоднородного продукта на разнородном транспорте

Для обеспечения перевозок может быть использовано s автохозяйств, в каждом из которых r типов автомашин. Машины разных типов, обладая различными эксплуатационными характеристиками и разной скоростью, могут доставлять любой из m грузов каждому из n потребителей.

Расстояние от места расположения g-го автохозяйства (g = 1,…., s) до пункта производства i-го груза (i = 1,…, m) известно. Известна скорость машин к-го типа (к = 1, …, r) для всех маршрутов. Известно время погрузки и разгрузки машин каждого типа в каждом пункте назначения. С учетом этой информации можно определить t_ijgk время занятости одной машины к-го типа g-го автохозяйства на работах по перевозке i-го груза j-му потребителю (или любые другие виды затрат, связанные с перевозкой единицы i-го груза в j-ый пункт назначения на одной машине к-го типа из g-го автохозяйства).

Параметры модели

a_gк – количество машин к-го типа в g-ом автохозяйстве;

c_ij – число единиц i-го груза, подлежащего перевозке j-му потребителю;

d_ij – число единиц i-го груза, которое перевозится в j-ый пункт назначения на одной машине (определяется по известной грузоподъемности машин).

Учет различной грузоподъемности машин приводит к распределительной задаче.

Требуется определить, сколько машин того или иного типа из какого автохозяйства следует направить для удовлетворения спроса каждого потребителя в каждом виде груза при минимальных суммарных затратах на перевозки (в автомобилечасах).

Примем х_ijgk – количество машин к-го типа из g-го автохозяйства, предназначенных для перевозки i-го груза j-му потребителю.

Математическая модель.

Определить значения переменных х_ijgk, на которых достигается минимум

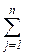
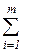
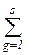
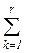t_ijgk х_ijgk → min

при условиях

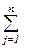
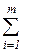х_ijgk ≤ а_gk,_, g = 1,…., s, к = 1, …, r - общее число машин к-го типа, направленных из g-го автохозяйства на перевозку всех грузов ко всем потребителям, не может превысить числа транспортных единиц к-го типа, которым располагает g-е автохозяйство;

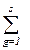
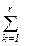d_ij х_ijgk = c_ij, i = 1,…, m, j = 1,…, n – спрос каждого пункта потребления в каждом виде груза должен быть полностью удовлетворен,

х_ijgk ≥ 0, i = 1,…, m, j = 1,…, n, g = 1,…., s, к = 1, …, r.

Полученная четырехиндексная задача путем преобразований может быть сведена к классической двухиндексной транспортной задаче достаточно общим для многих задач способом.

Каждый пункт, потребляющий m различных грузов рассматривается как группа из m различных пунктов, а автохозяйство с r типами машин учитывается как r автохозяйств. Соответственно определяются потребности каждого пункта назначения и возможности каждого транспортного подразделения.

Заменим пары индексов (i, j) и (g, к) двумя индексами λ и μ по следующим формулам:

λ = i + m (j – 1), μ = g + s (к – 1)

Когда индекс I пробегает значения 1,2, …, m, а j - значения 1,2, …, n, индекс λ принимает все целочисленные значения от 1 до mn. Индекс μ пробегает значения 1,2, …, sr.

Введем замену переменных х_ijgk = z_{λ μ}, i = 1,…, m, j = 1,…, n, g = 1,…., s, к = 1, …, r.

Обозначим t_ijgk через τ_{λ μ}, отношение c_ij / d_ij через g_λ, а_gk через b_μ.

В новых обозначениях задача сводится к вычислению переменных z_λμ, обращающих в минимум линейную форму

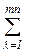
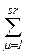τ_{λ μ} z_λμ → min

при условиях

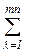z_λμ ≤ b_μ, μ = 1,2, …, sr,

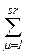z_λμ = g_λ, λ = 1,2,…, mn,

z_λμ ≥ 0, λ = 1,2,…, mn, μ = 1,2, …, sr.

Пришли к обычной транспортной задаче размеров mn х sr. По компонентам z_λμ оптимального плана задачи вычисляются составляющие х_ijgk. При этом индексы i и j вычисляются по формулам

m, если λ кратно m,

i = {остатку от деления λ на m, если λ не делится на m;

λ / m, если λ кратно m,

j = {целой части выражения (λ / m + 1), если λ не делится на m;

Аналогичным путем вычисляются индексы g и к.

Дата добавления: 2014-08-04; просмотров: 322; Нарушение авторских прав

Мы поможем в написании ваших работ!