Задача коммивояжера

Пример простой комбинаторной задачи – задача о назначениях. Здесь требование целочисленности выполняется автоматически, поскольку задача о назначениях представляет собой частный случай транспортной задачи (в котором m = n, a_i = b_j = 1). Более общий случай представляет собой задача коммивояжера.

Имеется n+1 городов; задана матрица С = 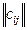расстояний между этими городами. Выезжая из исходного города (с номером 0), коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город 0. В каком порядке объезжать следует города, чтобы суммарное расстояние было минимальным?

Это напоминает задачу о назначениях (минимизация суммарного расстояния), но уже не по всем матрицам перестановок, что усложняет решение.

Параметры задачи

x_ij = 1, если коммивояжер из города i переезжает в город j,

x_ij = 0 в противном случае,

где i, j = 0, 1, 2, . . ., n.

Задача минимизации

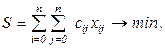(суммарное расстояние минимальное)

при условиях

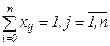(коммивояжер выезжает из каждого города, кроме начального, один раз)

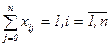(коммивояжер въезжает в каждый город, кроме начального, один раз)

u_i – u_j + nх_ij ≤ n - 1, 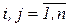, i ≠ j.

Здесь переменные u_i принимают целые неотрицательные значения. Последнее условие вводится для того, чтобы путь коммивояжера не распался на несколько не связанных между собой подциклов (задача о назначениях) – любой путь состоит из одного цикла.

Дата добавления: 2014-08-04; просмотров: 200; Нарушение авторских прав

Мы поможем в написании ваших работ!