
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Интерполяционные полиномы
Самым распространенным представлением функции в виде интерполяционного полинома является полиномиальный ряд:
L(t)=C0+C1t+C2t2+C3t3+...+Cntn . (2.1)
Если значения этого полинома приравнять значениям функции:
L(t0)=X0
L(t1)=X1
L(tn)=Xn ,
и вместо L расписать полностью полиномиальную зависимость (2.1), то получим систему алгебраических уравнений. Эту систему уравнений необходимо решить относительно коэффициентов С. Многочлен, получаемый из этой системы подстановкой решения относительно коэффициентов С, называют интерполяционным полиномом Лагранжа:
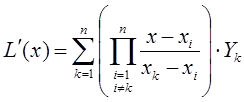 , (2.2)
, (2.2)
где П – знак произведения
ПРИМЕР.
Пусть имеются 3 значения функции:
| X | Y |
Определить полином Лагранжа.
N = 3 -- число дискрет;
n=2 =N-1 -- порядок полинома.
Следовательно, интерполяционный полином будет иметь вид
L(Х)=C0+C1X1+C2X22.
Ниже на графике даны пояснения коэффициентов и вид зависимости
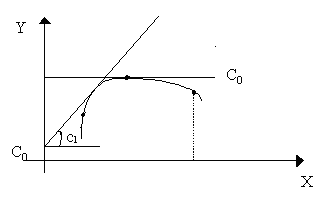
Рис. 2.4 График интерполяционного полинома
Подставляя в интерполяционный полином Лагранжа численные значения, получим
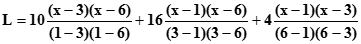 .
.
После преобразования зависимость будет иметь вид
L2(x)=2.8 - 8.6 x - 1.4 x2.
Полином Лагранжа позволяет сделать интерполяцию в узлах, расположенных на различных расстояниях. Если узлы будут находиться на одинаковых расстояниях, формула упростится в интерполяционный полином Ньютона.
Пример линейной и нелинейной интерполяции функции.

Рис. 2.5 График возможной интерполяционной функции
2.4 Вопросы для самоконтроля
1. В чем заключается задача интерполяции?
2. Поясните, что представляют собой дискреты?
3.Какая зависимость между количеством дискрет и порядком интерполирующего полинома?
4. Дайте определение конечной разности.
5. Какая связь существует между конечными разностями и дифференциалами?
6. Как определяются коэффициенты интерполяционного полинома?
7. Назовите интерполяционные полиномы.
| <== предыдущая страница | | | следующая страница ==> |
| Конечные разности | | | ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ |
Дата добавления: 2014-08-04; просмотров: 348; Нарушение авторских прав

Мы поможем в написании ваших работ!