ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

3.1 Основные характеристики обработки

экспериментальных данных

Результаты измерений имеют ошибки, определяемые неточностью приборов, погрешностью методики измерения, помехами в данных. Ошибки носят статистический характер, поэтому при обработке результатов используют методы математической статистики. При статистической обработке базовой характеристикой является плотность распределения вероятностей. Известно, что наиболее “шумящие” ошибки подчиняются нормальному закону распределения, кривая плотности распределения вероятностей которого имеет вид

Р(х) = 1/ sÖ2p*ехр(-(х-М(х))²/2s²).

Однако в практических приложениях вместо плотности распределения используют некоторые ее числовые характеристики, которые в основном описывают свойства аппроксимируемой плотности распределения. Перечислим их для ряда наблюдений

x₁ , x₂ ... x_n :

1) средняя величина - оценка математического ожидания.

;

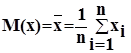2) дисперсия - оценивает разброс плотности распределения.

;

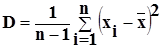3) среднеквадратическое отклонение - оценивает абсолютное отклонение значений переменных от математического ожидания.

.

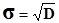Графически эти характеристики можно представить в виде трубки погрешности диаметром 2s и средним значением M[x].

Рис 3.1. Иллюстрация трубки погрешности

Для реального сигнала перечисленные характеристики будут отслеживать детерминированную составляющую и наложенную помеху.

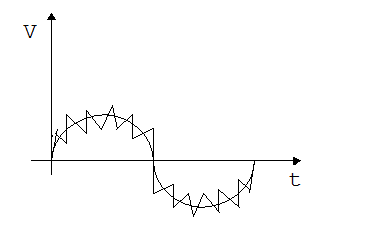
Рис 3.2 Сигнал с помехой

Для моделирования стохастических сигналов используют следующие виды анализов.

Гармонический анализ – для представления сигнала в виде ряда Фурье, если сигнал носит явный колебательный характер.

Корреляционный и автокорреляционный анализ - для определения линейных статистических взаимосвязей в сигнале.

Спектральный анализ – преобразование Фурье, для описания сигнала в частотной области.

Регрессионный анализ – для построения стохастической зависимости между входными и выходными переменными. Наиболее часто регрессионные уравнения рассматривают как функцию условного математического ожидания. При фиксированном х определяют математическое ожидание у - получают кривую регрессии, аналитическая форма которой определяется на основе методов аппроксимации или интерполяции. Дисперсия в этом случае характеризует отклонения значений зависимой переменной от ее условного математического ожидания.

Среднеквадратическое отклонение представляет трубку погрешности регрессионных уравнений или трубку нечувствительности измерения приборов.

Авторегрессионый анализ применяют для построения стохастических зависимостей между различными значениями времени, например, зависимостей, определяющих связь текущего значения функции от нескольких предыдущих. Значение количества временных дискрет (предыдущих), используемых в построении стохастической зависимости, называют глубиной памяти. На основе авторегрессионой зависимости можно прогнозировать значения стохастической зависимости.

Дата добавления: 2014-08-04; просмотров: 308; Нарушение авторских прав

Мы поможем в написании ваших работ!