
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Краткие сведения о системах счисления
Некоторые особенности представления чисел в различных системах счисления рассмотрены ниже.
Вспомним, что системой счисления называется система изображения чисел с помощью ограниченного набора символов. Обычно их представляют в виде последовательности цифр.
В цифровой технике используются позиционные системы счисления. Система счисления называется позиционной, если значение одной и той же цифры определяется ее позицией в изображении числа по некоторому закону. В соответствии с тем, что цифровые элементы, как уже было сказано выше, могут находиться в одном из строго заданных устойчивых состояний, в цифровой технике наибольшее распространение получила двоичная система счисления (формула 1.1).
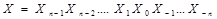 . (1.1)
. (1.1)
Таблица 1.1
Представление чисел в различных системах счисления
| Дес. | двоичн. | восьмеричн. | шестн. |
| 2 8 10 16 50 100 1000 5000 | 10 1000 1010 10000 110010 1100100 1111101000 1001110001000 | 2 10 12 20 62 144 1750 11610 | 2 8 А 10 32 64 3В8 1388 |
В табл. 1.1 приведено представление некоторых чисел в различных системах счисления.
Как видно из таблицы, двоичное изображение числа требует большего количества разрядов, чем, например, его десятичное представление. Но, тем не менее, наибольшее распространение в цифровой технике получила двоичная система счисления. Это обусловлено двумя факторами. Во-первых, простота двоичной арифметики. Вторым и наиболее важным достоинством двоичной системы является возможность использования для представления двоичного числа любого простого элемента, имеющего два устойчивых и четко разграниченных состояния: 0 и 1. Любое число Х в этой системе строится по правилу:
 , (1.2)
, (1.2)
где Хi принимает значения либо 0 либо 1, например:
1100101102=1*25+2*24+0*23+0*22+1*21+1*20+0*2-1+1*2-2+1*2-3=
=51,192510
В шестнадцатеричной системе счисления введены специальные обозначения для цифр больше девяти: десять – А; одиннадцать – В; двенадцать – С; тринадцать – D; четырнадцать – Е, пятнадцать – F. Например:
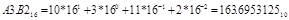
Примеры перевода чисел
из одной системы счисления в другую
Наиболее простым представляется перевод чисел из двоичной системы счисления к системам с основанием 8 и 16 и обратно. Например:
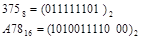 .
.
Обратный перевод состоит из двух действий. В зависимости от системы, в которую переводится двоичное число, производится разбиение разрядов, начиная с крайнего правого – младшего, на триады (к восьмеричной) и тетрады (шестнадцатеричной). Затем каждая из полученных групп переводится в цифры соответствующей системы счисления.
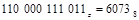 ,
,
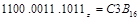 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Цифровая обработка радиосигналов | | | Понятие кодирования цифровой информации |
Дата добавления: 2014-02-26; просмотров: 437; Нарушение авторских прав

Мы поможем в написании ваших работ!